6.1.6: The Collision Theory
- Page ID
- 2236
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Collision theory explains why different reactions occur at different rates, and suggests ways to change the rate of a reaction. Collision theory states that for a chemical reaction to occur, the reacting particles must collide with one another. The rate of the reaction depends on the frequency of collisions. The theory also tells us that reacting particles often collide without reacting. For collisions to be successful, reacting particles must (1) collide with (2) sufficient energy, and (3) with the proper orientation.
Molecules must collide before they can react
This rule is fundamental to any analysis of an ordinary reaction mechanism. It explains why termolecular processes are so uncommon. The kinetic theory of gases states that for every 1000 binary collisions, there will be only one event in which three molecules simultaneously come together. Four-way collisions are so improbable that this process has never been demonstrated in an elementary reaction.

Consider a simple bimolecular step:
\[A + B \rightarrow Products \nonumber \]
If the two molecules A and B are to react, they must approach closely enough to disrupt some of their existing bonds and to permit the creation of any new ones that are needed in the products. Such an encounter is called a collision.
The frequency of collisions between A and B in a gas is proportional to the concentration of each; if [A] is doubled, the frequency of A-B collisions will double, and doubling [B] will have the same effect. If all collisions lead to products, then the rate of a bimolecular process is first-order in A and in B, or second-order overall:
\[rate = k[A][B] \nonumber \]
Not all Collisions are Equal
For a gas at room temperature and normal atmospheric pressure, there are about 1033 collisions in each cubic centimeter of space every second. If every collision between two reactant molecules yielded products, all reactions would be complete in a fraction of a second. For example, when two billiard balls collide, they simply bounce off of each other. This is the most likely outcome if the reaction between A and B requires a significant disruption or rearrangement of the bonds between their atoms. In order to effectively initiate a reaction, collisions must be sufficiently energetic (or have sufficient kinetic energy) to bring about this bond disruption. This is further discussed below.
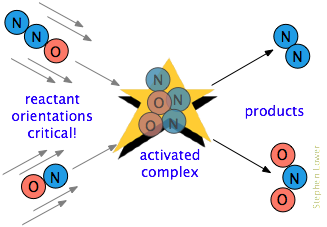
There is often one additional requirement. In many reactions, especially those involving more complex molecules, the reacting species must be oriented in a manner that is appropriate for the particular process. For example, in the gas-phase reaction of dinitrogen oxide with nitric oxide, the oxygen end of N2O must hit the nitrogen end of NO; altering the orientation of either molecule prevents the reaction. Owing to the extensive randomization of molecular motions in a gas or liquid, there are always enough correctly-oriented molecules for some of the molecules to react. However, the more critical this orientational requirement is, the fewer collisions will be effective.
Energetic collisions between molecules cause interatomic bonds to stretch and bend, temporarily weakening them so that they become more susceptible to cleavage. Distortion of the bonds can expose their associated electron clouds to interactions with other reactants that might lead to the formation of new bonds.
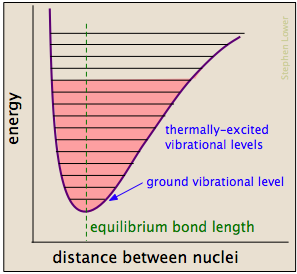
Chemical bonds have some of the properties of mechanical springs: their potential energies depend on the extent to which they are stretched or compressed. Each atom-to-atom bond can be described by a potential energy diagram that shows how its energy changes with its length. When the bond absorbs energy (either from heating or through a collision), it is elevated to a higher quantized vibrational state (indicated by the horizontal lines) that weakens the bond as its length oscillates between the extended limits corresponding to the curve.
A particular collision will typically excite a number of bonds in this way. Within about 10–13 seconds, this excitation is distributed among the other bonds in the molecule in complex and unpredictable ways that can concentrate the added energy at a particularly vulnerable point. The affected bond can stretch and bend farther, making it more susceptible to cleavage. Even if the bond does not break by pure stretching, it can become distorted or twisted so as to expose nearby electron clouds to interactions with other reactants that might encourage a reaction.
Unimolecular processes also begin with a collision
Until about 1921, chemists did not understand the role of collisions in unimolecular processes. It turns out that the mechanisms of such reactions are actually quite complicated, and that at very low pressures they do follow second-order kinetics. Such reactions are more properly described as pseudounimolecular. The cyclopropane isomerization described in Example 1 is typical of many decomposition reactions found to follow first-order kinetics, implying that the process is unimolecular.
Consider, for example, the isomerization of cyclopropane to propene, which takes place at fairly high temperatures in the gas phase.

The collision-to-product sequence can be conceptualized in the following [grossly oversimplified] way:

Note that
- For simplicity, the hydrogen atoms are not shown here. This is reasonable because C–C bonds are weaker then C–H bonds, which are less likely to be affected.
- The collision at
 is most likely with another cyclopropane molecule, but because no part of the colliding molecule gets incorporated into the product, it can in principle be a noble gas or some other non-reacting species;
is most likely with another cyclopropane molecule, but because no part of the colliding molecule gets incorporated into the product, it can in principle be a noble gas or some other non-reacting species; - Although the C–C bonds in cyclopropane are all identical, the instantaneous localization of the collisional energy can distort the molecule in various ways (
 ), leading to a configuration sufficiently unstable to initiate the rearrangement to the product.
), leading to a configuration sufficiently unstable to initiate the rearrangement to the product.
Here are some simple little "experiments" to help illustrate this concepts. These are "thought experiments," to be reasoned out rather than actually performed.
In an empty classroom, blindfold a group of 10 or so students and instruct them to walk slowly around the room. Occasionally, a pair of students will bump into one another. If they are moving slowly enough, nothing much will happen (that is, no pain upon contact). But if these blindfolded students begin running around the room (more speed means more energy), then a collision is likely to be successful (painfully so). If some students move about quickly, while others stroll about at a more leisurely pace, successful reactions will still occur, but not as often as if all students are running.
Next, have the students move at a brisk pace, but without running. This time, however, consider that collisions that occur shoulder-to-shoulder are not successful—shoulders act as sufficient bumpers and collisions are not painful. But if one student steps on another's toes, then a successful collision occurs. Let the movement begin. Of the frequent collisions that result, only a few will involve one student stepping on another's toes. This experiment illustrates that collisions must occur with the proper orientation. Again, collisions between students will occur, but only some will be successful.
Factors that increase the rate of a reaction must influence at least one of the following:
- how often collisions occur. More frequent collisions will mean a faster rate.
- more effective collisions in terms of collisions occurring with sufficient energy
- more effective collisions in terms of collisions occurring with the proper orientation.
Two more topics must be examined before these can be discussed in depth: reaction mechanisms and the concept of threshold energy.

