Phase Diagrams for Pure Substances
- Page ID
- 3864
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This page explains how to interpret the phase diagrams for simple pure substances - including a look at the special cases of the phase diagrams of water and carbon dioxide.
The Basic Phase Diagram
At its simplest, a phase can be just another term for solid, liquid or gas. If you have some ice floating in water, you have a solid phase present and a liquid phase. If there is air above the mixture, then that is another phase. But the term can be used more generally than this. For example, oil floating on water also consists of two phases - in this case, two liquid phases. If the oil and water are contained in a bucket, then the solid bucket is yet another phase. In fact, there might be more than one solid phase if the handle is attached separately to the bucket rather than molded as a part of the bucket.
You can recognize the presence of the different phases because there is an obvious boundary between them - a boundary between the solid ice and the liquid water, for example, or the boundary between the two liquids. A phase diagram lets you work out exactly what phases are present at any given temperature and pressure. In the cases we'll be looking at on this page, the phases will simply be the solid, liquid or vapor (gas) states of a pure substance. This is the phase diagram for a typical pure substance.
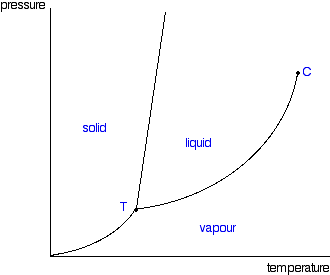
These diagrams (including this one) are nearly always drawn highly distorted in order to see what is going on more easily. There are usually two major distortions. We'll discuss these when they become relevant. If you look at the diagram, you will see that there are three lines, three areas marked "solid", "liquid" and "vapor", and two special points marked "C" and "T".
The Three Areas
These are easy! Suppose you have a pure substance at three different sets of conditions of temperature and pressure corresponding to 1, 2 and 3 in the next diagram.

Under the set of conditions at 1 in the diagram, the substance would be a solid because it falls into that area of the phase diagram. At 2, it would be a liquid; and at 3, it would be a vapor (a gas).
Phase Transitions
Moving from solid to liquid by changing the temperature
Suppose you had a solid and increased the temperature while keeping the pressure constant - as shown in the next diagram. As the temperature increases to the point where it crosses the line, the solid will turn to liquid. In other words, it melts.
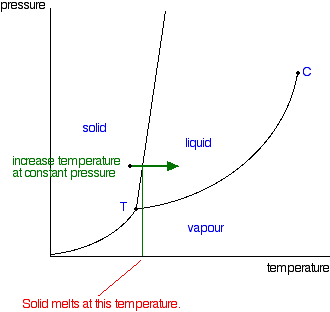
If you repeated this at a higher fixed pressure, the melting temperature would be higher because the line between the solid and liquid areas slopes slightly forward.
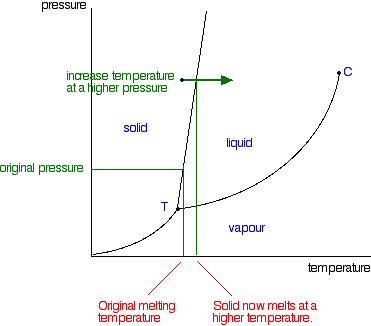
So what actually is this line separating the solid and liquid areas of the diagram?
It simply shows the effect of pressure on melting point. Anywhere on this line, there is an equilibrium between solid and liquid. You can apply Le Chatelier's Principle to this equilibrium just as if it was a chemical equilibrium. If you increase the pressure, the equilibrium will move in such a way as to counter the change you have just made.

If it converted from liquid to solid, the pressure would tend to decrease again because the solid takes up slightly less space for most substances. That means that increasing the pressure on the equilibrium mixture of solid and liquid at its original melting point will convert the mixture back into the solid again. In other words, it will no longer melt at this temperature.
To make it melt at this higher pressure, you will have to increase the temperature a bit. Raising the pressure raises the melting point of most solids. That's why the melting point line slopes forward for most substances.
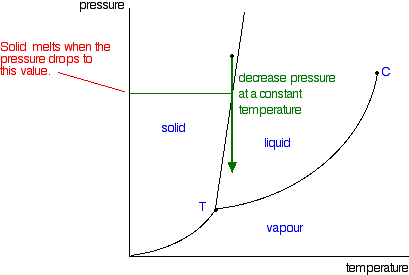
Moving from solid to liquid by changing the pressure
You can also play around with this by looking at what happens if you decrease the pressure on a solid at constant temperature.
Moving from liquid to vapor
In the same sort of way, you can do this either by changing the temperature or the pressure.
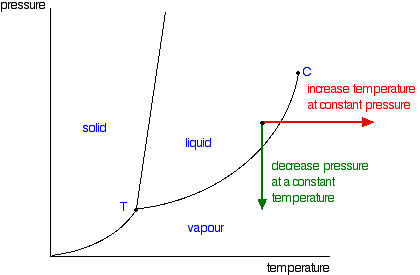
The liquid will change to a vapor - it boils - when it crosses the boundary line between the two areas. If it is temperature that you are varying, you can easily read off the boiling temperature from the phase diagram. In the diagram above, it is the temperature where the red arrow crosses the boundary line.
So, again, what is the significance of this line separating the two areas? Anywhere along this line, there will be an equilibrium between the liquid and the vapor. The line is most easily seen as the effect of pressure on the boiling point of the liquid. As the pressure increases, so the boiling point increases.
The critical point
You will have noticed that this liquid-vapor equilibrium curve has a top limit (labeled as C in the phase diagram), which is known as the critical point. The temperature and pressure corresponding to this are known as the critical temperature and critical pressure. If you increase the pressure on a gas (vapor) at a temperature lower than the critical temperature, you will eventually cross the liquid-vapor equilibrium line and the vapor will condense to give a liquid.
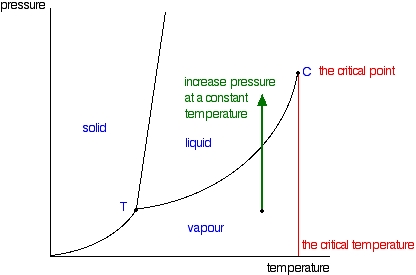
This works fine as long as the gas is below the critical temperature. What, though, if your temperature was above the critical temperature? There wouldn't be any line to cross! That is because, above the critical temperature, it is impossible to condense a gas into a liquid just by increasing the pressure. All you get is a highly compressed gas. The particles have too much energy for the intermolecular attractions to hold them together as a liquid. The critical temperature obviously varies from substance to substance and depends on the strength of the attractions between the particles. The stronger the intermolecular attractions, the higher the critical temperature.
Moving from solid to vapor
There's just one more line to look at on the phase diagram. This is the line in the bottom left-hand corner between the solid and vapor areas. That line represents solid-vapor equilibrium. If the conditions of temperature and pressure fell exactly on that line, there would be solid and vapor in equilibrium with each other - the solid would be subliming. (Sublimation is the change directly from solid to vapor or vice versa without going through the liquid phase.)
Once again, you can cross that line by either increasing the temperature of the solid, or decreasing the pressure. The diagram shows the effect of increasing the temperature of a solid at a (probably very low) constant pressure. The pressure obviously has to be low enough that a liquid can't form - in other words, it has to happen below the point labelled as T.
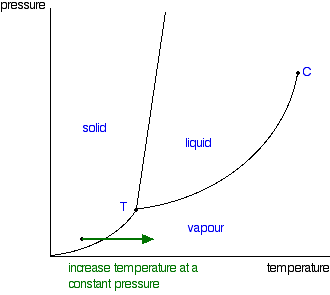
You could read the sublimation temperature off the diagram. It will be the temperature at which the line is crossed.
The Triple Point
Point T on the diagram is called the triple point. If you think about the three lines which meet at that point, they represent conditions of:
- solid-liquid equilibrium
- liquid-vapor equilibrium
- solid-vapor equilibrium
Where all three lines meet, you must have a unique combination of temperature and pressure where all three phases are in equilibrium together. That's why it is called a triple point.
If you controlled the conditions of temperature and pressure in order to land on this point, you would see an equilibrium which involved the solid melting and subliming, and the liquid in contact with it boiling to produce a vapor - and all the reverse changes happening as well. If you held the temperature and pressure at those values, and kept the system closed so that nothing escaped, that's how it would stay.
Normal melting and boiling points
The normal melting and boiling points are those when the pressure is 1 atmosphere. These can be found from the phase diagram by drawing a line across at 1 atmosphere pressure.
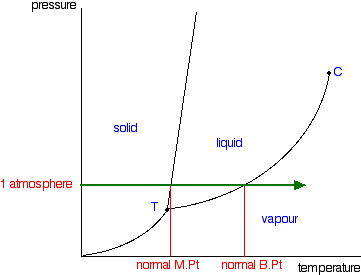
There is only one difference between this and the phase diagram that we've looked at up to now. The solid-liquid equilibrium line (the melting point line) slopes backwards rather than forwards.
In the case of water, the melting point gets lower at higher pressures. Why?
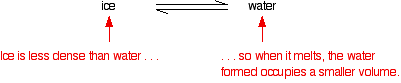
If you have this equilibrium and increase the pressure on it, according to Le Chatelier's Principle the equilibrium will move to reduce the pressure again. That means that it will move to the side with the smaller volume. Liquid water is produced. To make the liquid water freeze again at this higher pressure, you will have to reduce the temperature. Higher pressures mean lower melting (freezing) points.
Now lets put some numbers on the diagram to show the exact positions of the critical point and triple point for water.
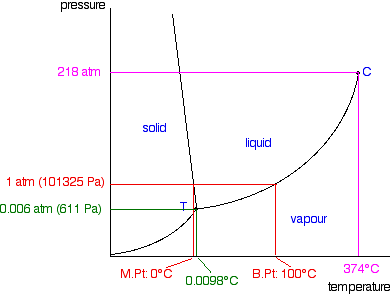
Notice that the triple point for water occurs at a very low pressure. Notice also that the critical temperature is 374°C. It would be impossible to convert water from a gas to a liquid by compressing it above this temperature. The normal melting and boiling points of water are found in exactly the same way as we have already discussed - by seeing where the 1 atmosphere pressure line crosses the solid-liquid and then the liquid-vapor equilibrium lines.
Just one final example of using this diagram. Imagine lowering the pressure on liquid water along the line in the diagram below.
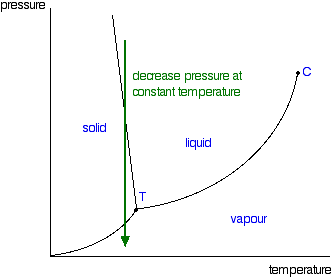
The phase diagram shows that the water would first freeze to form ice as it crossed into the solid area. When the pressure fell low enough, the ice would then sublime to give water vapor. In other words, the change is from liquid to solid to vapor.
The only thing special about this phase diagram is the position of the triple point which is well above atmospheric pressure. It is impossible to get any liquid carbon dioxide at pressures less than 5.11 atmospheres.
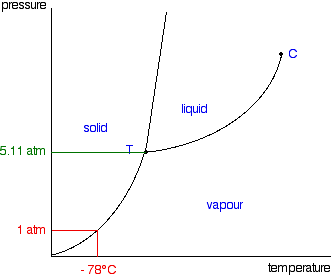
That means that at 1 atmosphere pressure, carbon dioxide will sublime at a temperature of -78°C. This is the reason that solid carbon dioxide is often known as "dry ice". You can't get liquid carbon dioxide under normal conditions - only the solid or the vapor.
Contributors and Attributions
Jim Clark (Chemguide.co.uk)


