Overview of Valence Bond Theory
- Page ID
- 2005
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Valence Bond (VB) Theory looks at the interaction between atoms to explain chemical bonds. It is one of the two common theories that helps describe the bonding between atoms. The other theory is Molecular Orbital Theory. Take note that these are theories and should be treated as such; they are not always perfect.
Introduction
Valence Bond Theory has its roots in Gilbert Newton Lewis’s paper The Atom and The Molecule. Possibly unaware that Lewis’s model existed, Walter Heitler and Fritz London came up with the idea that resonance and wavefunctions contributed to chemical bonds, in which they used dihydrogen as an example. Their theory was equivalent to Lewis’s theory, with the difference of quantum mechanics being developed. Nonetheless, Heitler and London's theory proved to be successful, providing Linus Pauling and John C. Slater with an opportunity to assemble a general chemical theory containing all of these ideas. Valence Bond Theory was the result, which included the ideas of resonance, covalent-ionic superposition, atomic orbital overlap, and hybridization to describe chemical bonds.
Atomic Orbital Overlap
Bonds are formed between atoms because the atomic orbitals overlap and that the electrons in those orbitals are localized within that overlap. They have a higher probability of being found within that bond; we will return to this statement when we talk about wavefunctions. Dihydrogen (H2) is a simple diatomic gas that has been used to illustrate this idea; however, let's look at Cl2 as a simple example. Cl has seven valence electrons. From its Lewis structure, one can see that Cl has a radical. That sole radical indicates that Cl can bond once. As a general rule, the number of unpaired electrons denotes how many bonds that atom can make. Since there is only one unpaired electron in each Cl, those electrons interact to bond. In this case, the 3p orbitals overlap. Lone pairs can be seen as the orbitals not interacting with each other. The idea of atomic orbitals overlapping works well for simple molecules, such as diatomic gases, but more complex molecules cannot be explained simply by the overlap of atomic orbitals, especially if they defy the octet rule when drawing out Lewis structures and if they bond beyond their predicted amount.
One small concept to add in here is that an orbital from one atoms can be overlap with the other orbital of the second atom. This will eventually give one of the two results. First, the two orbitals have correct symmetry to interact or "mix" (4). Second, the two orbitals do not have correct symmetry to interact or "mix" (4). In the case of two orbitals do not interact, there will be no bonding interaction, which means one of the atomic orbitals will not contribute into the bonding. Another word, it will not affected because of the presence of other atomic orbitals. For further explaination, when the two wavefunctions are knowns as constructive interaction, which means the orbitals do not interact with one another. And if the two orbitals are interacting, they are knowns as destructive interaction where their wavefunctions have opposite site (4).
In the case of two orbitals do interact with each others, it will become molecular orbitals, and it is knowns as constructive interaction, resulting bonding orbitals. On the other hand, if destructive interaction, it will create an antibonding interaction. The two molecular orbitals are the result from adding and subtracting the two wavefunctions (4).
Atomic Orbital Hybridization
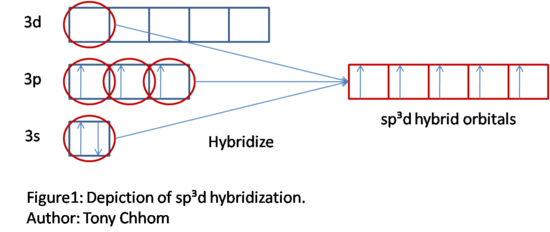
Consider phosphorus pentaflouride (PF5). P, the central atom, has five valence electrons, with three lone electrons. Thus, P should only be able to form three bonds. However, in order for PF5 to exist with P as the central atoms, P must be able to bond five times. This event is described by orbital hybridization. In order to create degenerate hybrid orbitals that allow atoms to bond well beyond their normal amount. Orbitals involved in hybridization are the s, p, and d atomic orbitals. There are certain principles that must be followed:
- Orbitals are not magically lost or gained. The number of orbitals mixed must match the number of hybrid orbitals acquired.
- Always start from an s orbital. Build your way up to p orbitals, and then d orbitals as necessary. These are orbitals from the atom in question. In this case, it is the P atom.
Hybrid orbitals consist of sp, sp2, sp3, sp2d, sp3d, and sp3d2 (3). Returning back to PF5, let's see how hybrid orbitals can describe its bonds. Remember that P can only bond three times, but we need it to bond five times. In order to bond five times, five orbitals must be singularly filled in. Bonds occur when orbitals with only one electron are spin paired with the electron from another atom. The five orbitals can be acquired by sp3d orbital hybridization. Starting off with a total of five orbitals will result in five hybrid orbitals. Note that since P is in period 3, it has d orbitals in the same energy level. Thus, 3d orbitals can be used to hybridize, even though electrons do not occupy it. The process is outlined in the original figure below. Remember to follow the aufbau principle, Hund's rule, and the Pauli exclusion principle when assigning electrons to their orbitals. Note that valence electrons are only shown. Other orbitals and their corresponding electrons are not hybridized and are not involved in bonding. Although they are not shown, they still exist.
Now, P has five hybrid orbitals. Remember that P has five valence electrons. Electrons too are not lost or gained, so those electrons transfer over to the hybrid orbitals. Fill them in accordingly, following Hund's rule and the Pauli exclusion principle. Note that the hybrid orbitals are now degenerate, so the aufbau principle doesn't apply for this case. From sp3d hybridization, P has five unpaired electrons and can now bond with five F.
Generally, if two bonds are needed, then use an sp; for three, use sp2; the number of bonds needed equals the number of orbitals that need to be hybridized. Please take into account that lone pairs apply as well. If there is a lone pair when you complete the Lewis structure, then the number of required hybrid orbitals equals the number of lone pairs plus the number of bonds; this is also called the coordinate number. PF5, although not shown, does not have lone pairs. The type of hybrid orbitals also corresponds to the molecular shape. In the case of PF5, its shape as defined by VSEPR is trigonal bypyramidal. If hybrid orbitals are involved, the shape can also be determined by the type of hybridization. As another example, sp is linear, and sp2 is trigonal planar. sp2d is square planar. Think over carefully why the type of hybridization also determines the shape. An example problem will aid you in your thinking in the problems section.
How the wavefunction Applies to VB Theory
The wavefunction describes the state of an electron. From the name of the function, one can derive that the electron can behave like a wave. This wave-like behavior of the electrons defines the shapes of the orbitals. Thus, it makes sense that wavefunctions are related to the Valence Bond Theory. If orbitals overlap to create bonds, and orbital shapes and the state of an electron is described by the wavefunction, then it makes sense that the overlap of orbitals (the bonds) can be described by wavefunctions as well. Thus, covalent and ionic bonds can be described by wavefunctions. Covalent and ionic representations of a bond represent the same bond, but they differ in how the electro ns are placed. This is called resonance. Different intermolecular interactions give rise to different wavefunctions. Recall from Hund's Rule and the Pauli exclusion principle that electrons must be spin paired when the right conditions are met. Due to this, there are two separate ways to represent a covalent bond in terms of electron spin, which is related to the wavefunction. The figure shows the two different cases for two electrons in a bond. Thus, it is possible to write two different wavefunctions that describe each case, which can be superimposed to describe the overall covalent bond (2). The superposition of the covalent bond and ionic bond wavefunctions will result in an overall wavefunction that describes the state of the molecule. Due to this module being an overview of Valence Bond Theory, the full details will not be covered.
ns are placed. This is called resonance. Different intermolecular interactions give rise to different wavefunctions. Recall from Hund's Rule and the Pauli exclusion principle that electrons must be spin paired when the right conditions are met. Due to this, there are two separate ways to represent a covalent bond in terms of electron spin, which is related to the wavefunction. The figure shows the two different cases for two electrons in a bond. Thus, it is possible to write two different wavefunctions that describe each case, which can be superimposed to describe the overall covalent bond (2). The superposition of the covalent bond and ionic bond wavefunctions will result in an overall wavefunction that describes the state of the molecule. Due to this module being an overview of Valence Bond Theory, the full details will not be covered.
The wavefunction squared will result in a probability density. The wavefunction alone has no physical significance; however, when the wavefunction is squared, the square wavefunction can determine where the electron is most likely located. Recall that when atomic orbitals overlap, the electrons are localized and more likely to be found within that overlap. In terms of electrostatic interactions, this bond will result in some form of equilibrium between all of the electrostatic forces (between the electrons and the electrons with each nucleus) (1). If the overlap is too far in, there is a net repulsion force; the electrons will also be forced apart. If the atomic orbital overlap is too small, the net attraction force is very small; the electron will have a smaller chance of remaining in the overlap since they will be more attracted to their own nucleus. If the overlap is just right, then the electrons are attracted to both nuclei and more likely to stay in the overlapped area. Thus, wavefunctions and electrostatic forces can both explain why electrons are localized within their bonds.
Reliability of Valence Bond Theory and Uses
As one can see, Valence Bond Theory can help describe how bonds are formed. However, there are some notable failures when it comes to Valence Bond Theory. One such failure is dioxygen. Valence Bond Theory fails to predict dioxygen's paramagnitism; it predicts that oxygen is diamagnetic. A species is paramagnetic if electrons are not spin paired and diamagnetic if the electrons are spin paired. Since Valence Bond theory begins with the basis that atomic orbitals overlap to create bonds and through that reasoning, one can see that electrons are spin paired when bonds overlap, dioxygen is indeed predicted to be diamagnetic if Valence Bond Theory is used. In reality, that is not the case. Also, sp2d and sp3 both have a coordinate number of four. Thus, Valence Bond Theory cannot predict whether the molecule is a square planar or the other shape (3). One must correctly draw the Lewis structure and use VSEPR to determine the shape.
References
- Kotz, John C., Paul M. Treichel., John R. Townsend. Chemistry and Chemical Reactivity. 7th ed. Australia: Thomson Brooks/Cole., 2009. Print.
- Shaik, Sason S., Hiberty, Philippe C. A Chemist's Guide to Valence Bond Theory. Hoboken, New Jersey: Wiley, 2008. Print.
- Wijesekera, Ramanee D. Coordination Compounds: Bonding, Structure and Nomenclature. Oxford, U.K.: Alpha Science International Ltd., 2008. Print.
- Overlap of Atomic Orbitals to form Molecular Orbitals. www.chm.davidson.edu/vce/MolecularOrbitals/overlap/overlap1.html
Problems
- Draw the Lewis structures HF, CO2, and C2H2. Which orbitals are involved with bonding for HF? Now, use hybridization to explain the bonds of CO2 and C2H2. Can you account for the single, double, and triple bonds via orbitals overlapping and hybridization? It is not required to draw the hybridization process, but it might help you in your thinking.
- Using VSEPR, one can derive that IBr5 has an octahedral parent shape. Now, use Valence Bond Theory to account for all of the bonds and verify that the parent shape is indeed an octahedral. Why can you determine the parent shape of a molecule based on Valence Bond Theory? Show your work.
- Determine the family shapes correlated with the sp3, sp3d, and sp3d2 hybridization. Does this mean that all molecules with the respectable hybridization will have the same shape? Explain.
- Predict which of these atoms/molecules is diamagnetic using Valence Bond Theory: H, H2, and NO.
- Briefly summarize Valence Bond Theory. Is it always reliable?
Solutions
HF: Hydrogen has one electron in the 1s orbital. Flourine has two electrons in the 2s orbital, and five in the 2p orbitals. These can be derived from the electron configurations. We are only interested in the valence electrons, so the lower shell can be ignored. Remember to fill in the orbitals accordingly. The orbitals availiable to bond are Hydrogen's 1s orbital and one of Flourine's 2p orbitals. Thus, the bond must take place between these two orbitals. This is a sigma bond. A bond of this type, or one of similar orientation, such as two s orbitals, are the bonds associated with hybrid orbitals when hybridization takes place.
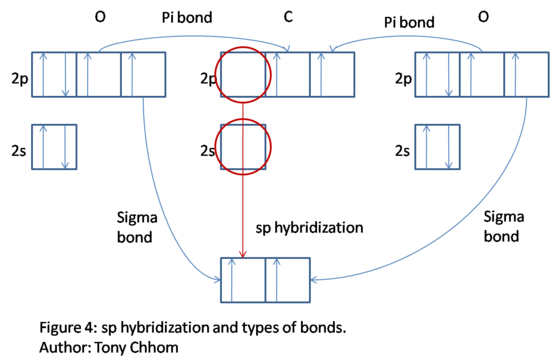
CO2: C has four valence electrons; two are in 2s and two are in 2p. O has six valence electrons; two in 2s and four in 2p. Notice that there is a double bond. Now, hybridize to explain the bonds. When determining the coordinate number, double bonds and triple bonds count as one bond. Thus, the coordinate number of C is 2 and the corresponding hybridization is sp. The diagram below shows the sp hybridization process for C. Notice that two 2p orbital remains unhybridized. We fill in the hybrid orbitals with two of C's electrons so that C has space available to bond with the two O's. The hybrid orbitals describes two sigma bonds between C and the O's; one 2p orbital from each O is used in this process. Two electrons remain for C, which are allocated to the unhybridized orbitals. Now, C can form the other two bonds for a total of four which is what is expected due to the presence of two double bonds. The unhybridized orbitals overlap O's 2p orbitals and forms what is called a pi bond. There is one pi bond and one sigma bond between C and each O. The lone pairs of the O's are the filled 2s orbital and the final and filled 2p orbital. Thus, a double bond is explained by one sigma bond associated with the hybrid orbitals and a pi bond associated with unhybridized p orbitals.
C2H2: C has four valence electrons (two in 2s and two in 2p) and H has one (one in 1s). There is a total of ten valence electrons. From the Lewis structure, one can see that there is a triple bond between the two C's. For each C, one can explain the bonds through sp hybridization (a triple bond and one single bond). This process is similar to CO2. However, in this case, C's available unhybridized 2p orbitals bond together with the unhybridized p orbitals of the other C. Now, there are two pi bonds and one sigma bond between the C's; there is one sigma bond between each C and H bond. Thus, a triple bond is explained by one sigma bond associated with the hybrid orbitals and two pi bonds associated with unhybridized p orbitals.
2. I is the central atom. Usually, the least electronegative atom is the central atom. Drawing the Lewis structure reveals that I can only form one bond. However, with the use of hybridization, I can form more bonds. Showing that is the goal. First, find out how many valence electrons IBr5 has. This is simply derived by adding all of the valence electrons from each atom; all have 7 valence electrons, so (6)(7)=42. Then, use Lewis structure and allocate all of the electrons into the correct places. You will find that the Lewis structure looks like the picture below.
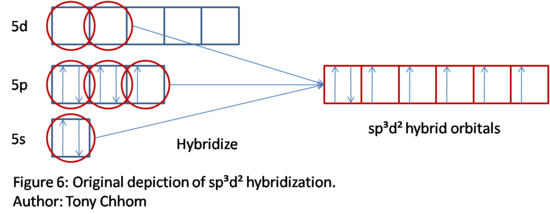
Notice that there is a lone pair. Remember that the number of hybrid orbitals needed is the summation of lone pairs and bonds. This is a total of six; thus a sp3d2 hybridization is needed. This process is shown below. Take note that the lone pair is the only spin paired electrons in the hybrid orbitals. Since the coordinate number is six, then the family shape of this molecule is an octahedral shape. Even the lone pairs are accounted for when hybridization takes place. It is because we used the coordinate number (determined by using Lewis dot structure first) to determiine the type of hybridization that hybridization does indeed give the correct family shape. There are of course exceptions, such as sp2d and sp3. We cannot predict the shape based on hybridization alone for these.
3. The shapes are tetrahedral, trigonal bypyramidal, and octahedral respectively. Not all molecules will have the shape associated with the hybridization type because lone pairs must be taken into account as well. For example, look at problem number two. The coordinate number is six. That tells you that the parent shape is an octahedral. However, the shape of IBr5 will only be that shape if the lone pair was another atom. The parent shape will not always match the actual shape of the molecule. It gives you a place to start and is only true if lone pairs do not exist. "Removing" one bond away from the octahedral shape will give the result of the square-base pyramidal shape.
4. One can solve this problem simply by counting the valence electrons. H has only one electron; it is not paired with any other electron and thus must be paramagnetic. H2 has two valence electrons; thus, those electrons are spin paired and H2 is diamagnetic. NO has eleven valence electrons; it is paramagnetic. In general, if an atom/molecule has an odd number of electrons, then that atom/molecule is paramagnetic. It is diamagnetic if it has an even number of electrons; however, like the case of O2, this does not always work.
5. Valence Bond Theory looks at the interaction between orbitals to describe bonds. It can also be used to derive the shape of the molecule in question, as well as determining whether or not an atom/molecule is diamagnetic or paramagnetic; however Valence Bond Theory is not always reliable. It fails in some cases. One must always remember that this is a theory.