Hybrid Orbitals in Carbon Compounds

Last updated
Save as PDF

Page ID: 32850

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Learning Objectives

Describe the hybrid orbitals used in the formation of bonding for each atom in some carbon containing compounds.
Calculate formal charge for each atom in some carbon containing compounds.
Draw resonance structures for some organic compounds.

Diamond crystals such as the one shown here are appreciated by almost everyone, because of their hardness, sparkle, and high value. They are also important in many technical applications. However, in terms of chemistry, diamonds consist of only carbon atoms, except for impurities. Like diamond, the chemistry of carbon is indeed very interesting and valuable.

Carbon atoms have the ability to bond to themselves and to other atoms with sp, sp², and sp³ hybrid orbitals. This link gives you the basics about the hybrid orbitals, and you are introduced to the various bonding of carbon in this document. Compounds containing carbon-hydrogen bonds are called organic compounds. They may also contain \(\ce{C-C}\), \(\ce{C=C}\), \(\ce{C\equiv C}\), \(\ce{C-N}\), \(\ce{C=N}\), \(\ce{C\equiv N}\), \(\ce{C-O}\), and \(\ce{C=O}\) bonds. Such a variety is due to the ability of carbon to make use of sp, sp², and sp³ hybrid orbitals for the bonding. There are also various inorganic compounds such as carbon monoxide, carbon dioxide, calcium carbonate, sodium bicarbonate, etc. involving carbon.

Carbon Atoms Using sp Hybrid Orbitals

When sp hybrid orbitals are used for the sigma bond, the two sigma bonds around the carbon are linear. Two other p orbitals are available for pi bonding, and a typical compound is the acetylene or ethyne \(\ce{HC\equiv CH}\). The three sigma and two pi bonds of this molecule from University of Florida: General chemistry are shown below.

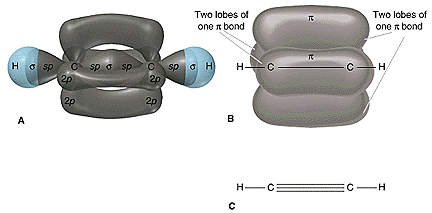
Note that molecules \(\ce{H-C\equiv C-H}\), \(\ce{H-C\equiv N}\), and \(\ce{C\equiv O}\) have the same number of electrons. Bonding in these molecules can be explained by the same theory, and thus their formation is no surprise. The \(\ce{O=C=O}\) molecule is linear, and the carbon atom in this molecule also involves the sp hybrid orbitals. Two pi bonds are also present in this simple molecule. As an exercise, draw a picture to show the two sigma and two pi bonds for this molecule.

Carbon Atoms Using sp² Hybrid Orbitals

When carbon atoms make use of sp² hybrid orbitals for sigma bonding, the three bonds lie on the same plane. One such compound is ethene, in which both carbon atoms make use of sp² hybrid orbitals. One of the remaining p orbitals for each carbon overlap to form a pi bond. A pi bond consists of two parts where bonding electrons are supposed to be located. A picture depicting the sigma and pi bonds in ethene from the same source as the previous picture is shown on the right.

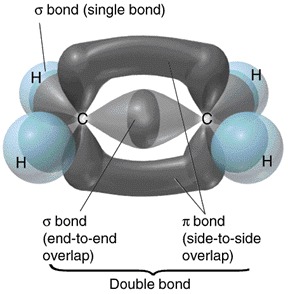
Carbon atoms make use of sp² hybrid orbitals not only in ethene, but also in many other types of compounds. The following are some of these compounds:

Formaldhyde	Ketene	Ethylaldehyde	Acetic acid	Benzene	Others
H \ C=O / H	H \ C=C=O / H	CH₃ \ C=O / H	CH₃ \ C=O / O-H	CH / \\ HC CH \|\| \| HC CH \ // CH	Arromatic compounds Graphite Fullerenes

Formaldhyde

Ketene

Ethylaldehyde

Acetic acid

Benzene

Others

H
\
C=O
/
H

H
\
C=C=O
/
H

CH₃
\
C=O
/
H

CH₃
\
C=O
/
O-H

CH
/ \\
HC CH
|| |
HC CH
\ //
CH

Arromatic
compounds

Graphite

Fullerenes

During the lecture on covalent bonding, we can illustrate how atomic orbitals overlap in the formation of bonds. Here, we can only show you the nice picture as a result.

Carbon Atoms Using sp³ Hybrid Orbitals

In ethane, the carbon atoms use sp³ hybrid orbitals for the formation of sigma bonds. The four bonds around each \(\ce{C}\) atom point toward the vertices of a regular tetrahedron, and the ideal bond angles are 109.5°. The simplest compound is methane, \(\ce{CH4}\), which is the first member of the alkane family. The next few members are ethane, \(\ce{CH3CH3}\), propane, \(\ce{CH3CH2CH3}\), butane, \(\ce{CH3CH2CH2CH3}\), etc..

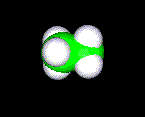
H H \ / H--C---C--H / \ H H

Diamond is a crystal form of elemental carbon, and the structure is particularly interesting. In the crystal, every carbon atom is bonded to four other carbon atoms, and the bonds are arranged in a tetrahedral fashion. The bonding, no doubt, is due to the sp³ hybrid orbitals. The bond length of 154 pm is the same as the \(\ce{C-C}\) bond length in ethane, propane and other alkanes.

An idealized single crystal of diamond is a gigantic molecule, because all the atoms are inter-bonded. The bonding has given diamond some very unusual properties. It is the hardest stone, much harder than anything else in the material world. It is a poor conductor, because all electrons are localized in the chemical bonds. However, diamond is an excellent heat conductor. A stone made of pure carbon is colorless, but the presence of impurities gives it various colors. The index of refraction is very high, and their glitter (sparkle or splendor) has made them the most precious stones.

Comparison of Structural Features

Some typical bonding features of ethane, ethene, and ethyne are summarized in the table below:

Systematic name	Ethane	Ethene	Ethyne
Hybrid orbitals of \(\ce{C}\)	sp³	sp²	sp
Structural formula	H H \ / H--C---C--H / \ H H	H H \ / C=C / \ H H	H-C≡C-H
\(\ce{C-C}\) Bondlength pm	154	134	120
\(\ce{C-H}\) Bondlength pm	112	110	106
\(\ce{H-C-C}\) bond angle °	111	121	180
\(\ce{C-C}\) bond energy kJ/mol	368	611	820
\(\ce{C-H}\) bond energy kJ/mol	410	451	536

As the bond order between carbon atoms increases from 1 to 3 for ethane, ethene, and ethyne, the bond lengths decrease, and the bond energy increases. Note that the bond energies given here are specific for these compounds, and the values may be different from the average values for this type of bonds.

Confidence Building Questions

What hyprid orbitals are used by the carbon atoms in \(\ce{HC\equiv CH}\)?

Hint: sp hybrid orbitals

Discussion -
Linear \(\ce{-C -}\) bonds due to sp hybridized orbitals. This molecule is linear, and it consists of 3 sigma, s, bonds, and two pi, p, bonds. Compare the bonding of this with \(\ce{C\equiv O}\), \(\ce{H-C\equiv N}\), and \(\ce{CH3-C\equiv N}\).
What hyprid orbitals are used by the carbon atoms in \(\ce{H2C=CH2}\)?

Hint: sp² hybrid orbitals

Discussion -
Planar \(\ce{-C}\textrm{<}\) bonds due to sp² hybridized orbitals. Another p orbital is used for the pi, p. How many sigma and pi bonds does this molecule have? Do all atoms in this molecule lie on the same plane?
What hyprid orbitals are used by the carbon in \(\ce{CH3CH3}\)?

Hint: sp³ hybrid orbitals

Discussion -
Tetrahedral arrangement around \(\ce{C}\) is due to sp³ hybridized orbitals.
What hyprid orbitals are used by the oxygen in \(\ce{CH3CH2OH}\)?

Hint: sp³ hybrid orbitals

Discussion -
Tetrahedral arrangement around \(\ce{C}\) is due to sp³ hybridized orbitals.
Which carbon to carbon bond length is the shortest in the following molecule: \(\ce{CH3CCCH2CHCHCH2OH}\)?

Hint: shortest between triple bonded carbon

Discussion -
The bond length decreases as the bond order increases.
How many carbon atoms make use of sp² hybrid orbitals in this molecule: \(\ce{CH3CCCH2CHCHCH2COOH}\)?

Hint: three

Discussion -
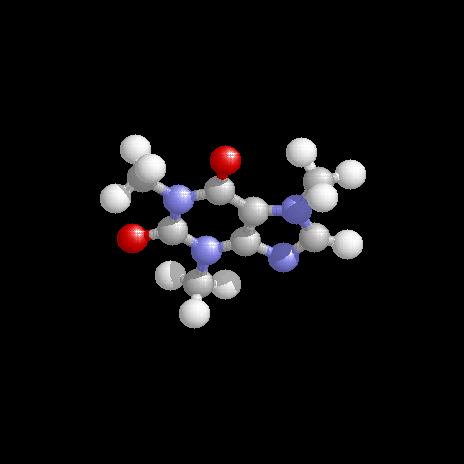
Recognize the type of bonding is important.
The molecular formula of caffeine is \(\ce{C8H10N4O2}\); draw a reasonable structure for it.

Hint: This is one of the problems for chemists.

Discussion -
The structure is shown below. Can you sketch a bonding structure for caffeine? How many carbon atoms makes use of sp² hybrid orbitals?

Contributors and Attributions

Chung (Peter) Chieh (Professor Emeritus, Chemistry @ University of Waterloo)