MO for HF
- Page ID
- 37502
Molecular Orbitals for Heterogeneous Diatomic Molecules
A simple approach to molecular orbital (MO) theory for heterogeneous diatomic molecules is to show the energy level diagram. The MO energy levels can be worked out following these steps:
Recall that the energy \(E_n\) for the quantum number n is for an element with atomic Z is approximately
\[E_n = 13.6 \dfrac{Z_{Eff}^2}{n^2} eV\]
We use \(Z_{eff}\) instead of Z to mean that we have to modify the atomic number to get an effective atomic charge for the nucleus. Since we are dealing with approximate values, one may use Z directly. The 1s orbital energy level is -13.6 eV for hydrogen atoms, measured as the ionization energy of H.
Thus, for the quantum number n = 1, the energy level for 1s of He is approximately - 54 eV. Similarly, the 1s energy level for F is - 1101 eV. The 2s and 2p energy levels for He is approximately - 13.6 eV, which is simlar to that of 1s orbital of H.
Thus, the 2s energy level for Li is approximately -6 eV. However, for multi-electron atoms, the p-subshell and s-subshell have different energies due to penetration. At this level, we cannot be precise about it, but simply think that the 2p orbitals are at higher energy than the 2s orbital. Usually, atomic orbitals with energy levels similar to each other will overlap to form molecular orbitals. Thus, we match the energy levels of atomic orbitals, and then make bonding and anti-bonding MOs of them.
However, in case the atomic orbital energy level is very different, we use atomic orbitals of the incomplete subshell to form MOs.
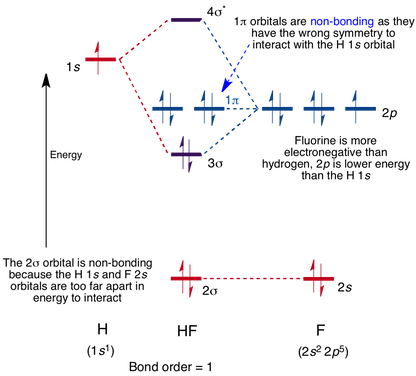
Molecular Orbital Diagram for the HF Molecule
Interaction occurs between the 1s orbital on hydrogen and the 2p orbital in fluorine causing the formation of a sigma-bonding and a sigma-antibonding molecular orbital, as shown below.
Contributors and Attributions
Chung (Peter) Chieh (Professor Emeritus, Chemistry @ University of Waterloo)