Water Autoionization
- Page ID
- 1294
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Water, even pure water, has an amphiprotic nature. This means that a small amount of ions will form in pure water. Some molecules of H2O will act as acids, each donating a proton to a corresponding H2O molecule that acts as a base. Thus, the proton-donating molecule becomes a hydroxide ion, OH-, while the proton-accepting molecule becomes a hydronium ion, H3O+.
Introduction
Water molecules are amphiprotic and can function as both acids and bases. One water molecule (acting as a base) can accept a hydrogen ion from a second water molecule (acting as an acid). This will be happening anywhere there is even a trace of water - it does not have to be pure. A hydronium ion and a hydroxide ion are formed.
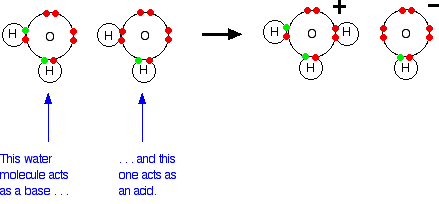
However, the hydroxonium (used unambiguously with hydronium) ion is a very strong acid, and the hydroxide ion is a very strong base; in fact, they are the strongest in water. As fast as they are formed, they react to produce water again. The net effect is that an equilibrium is set up:
\[2H_2O\,(l) \rightleftharpoons H_3O^+ \,(aq) + OH^- \, (aq) \tag{1}\]
At any one time, there are incredibly small numbers of hydroxonium ions and hydroxide ions present. Further down this page, we shall calculate the concentration of hydroxonium ions present in pure water. It turns out to be 1.00 x 10-7 mol dm-3 at room temperature. This equilibrium written in a simplified form:
\[H_2O\,(l) \rightleftharpoons H^+ \,(aq) + OH^- \, (aq) \tag{2}\]
with H+(aq) actually referring to a hydronium ion.
It is important to remember that water contains VERY low concentration of these ions. In the reversible reaction:
\[\underset{\text{base 1}}{H_2O} + \underset{\text{acid 2}}{H_2O} \rightleftharpoons \underset{\text{acid 1}}{H_3O^+} + \underset{\text{base 2}}{OH^-} \tag{4}\]
the reaction proceeds by far to the left. Pure water will dissociate to form equal concentrations (here, we are using molarities) of hydronium and hydroxide ions, thus:
\[ [H_3O^+] = [OH^-] \tag{5}\]
For this equation, we can find K, the equilibrium constant:
\[K= [H_3O^+][OH^-] \tag{6}\]
At standard temperature and pressure (STP), the equilibrium constant of water, \(K_w\), is equal to:
\[K_w= [H_3O^+][OH^-] \tag{7}\]
\[K_w=[1.0 \times 10^{-7}][1.0 \times 10^{-7}]\tag{8} \]
\[K_w=1.0 \times 10^{-14} \tag{9}\]
In this equation, [H3O+] is the concentration of hydronium ions which, in a chemical equation, is the acid dissociation constant, \(K_a\). The [OH-] is the concentration of hydroxide ions which, in a chemical equation, is the base constant, \(K_b\). If given a pH, then you can easily calculate the [H3O+] by:
\[[H_3O^+] = 10^{-pH}. \tag{10}\]
The same formula applies to obtaining [OH-] from the pOH:
\[ [OH-]=10^{-pOH} \tag{11}\]
Adding the pH's gives you the \(pK_w\)
\[pK_w= pH + pOH =14.00 \tag{11}\]
Since the reaction proceeds so heavily to the left, the concentration of these hydroxide and hydronium ions in pure water is extremely small. When making calculations determining involving acids and bases in solution, you do not need to take into account the effects of water's autoionization unless the acid or base of interest is incredibly dilute. However, it is interesting to note that water's self-ionization is significant in that it makes the substance electrically conductive.
In the equation depicting the autoionization of water,
\[ H_2O + H_2O \rightleftharpoons H_3O^+ + OH^- \]
The reaction proceeds far to the __________.
Solution
left. The concentration of hydroxide and hydronium ions in pure water is very, very small. Although it is rarely something you need to worry about when looking at acids and bases in solution, it does help account for certain properties of water, such as electrical conductivity.
If a solution has a pH of 2.1, determine the concentration of hydroxide ions, [OH-].
Solution
To solve for this, you must first determine the concentration of the hydronium ion, [H3O+]:
[H3O+] = 10-pH
= 10-2.1
= 7.94 x 10-3
Then, you solve for [OH-] using the Kw constant:
Kw = [H3O+] [OH-]
1.0 x 10-14 = [OH-][7.94 x 10-3]
[OH-] = (1 x 10-14) / (7.94 x 10-3)
= 1.26 x 10-12
If an aqueous solution has a pOH of 11.2, determine the concentration of hydronium ions.
Solution
To solve for this, you must first determine the concentration of the hydroxide ion, [OH-]:
[OH-] = 10-pOH
= 10-11.2
= 6.31 x 10-12
Then, you solve for [H3O+] using the Kw constant:
Kw = [H3O+] [OH-]
1.0 x 10-14 = [H3O+][6.31 x 10-12]
[H3O+]= (1 x 10-14)/ (6.31 x 10-12) = 0.00158
References
- Petrucci, et al. General Chemistry: Principles & Modern Applications. 9th ed. Upper Saddle River, New Jersey: Pearson/Prentice Hall, 2007.
Contributors and Attributions
- Katherine Dunn (UCD), Hannah Walker (UCD)
Jim Clark (Chemguide.co.uk)


