The pH Scale
- Page ID
- 1291
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To define the pH scale as a measure of acidity of a solution
- Tell the origin and the logic of using the pH scale.
- Apply the same strategy for representing other types of quantities such as pKa, pKb, pKw.
Auto-Ionization of Water
Because of its amphoteric nature (i.e., acts as both an acid or a base), water does not always remain as \(H_2O\) molecules. In fact, two water molecules react to form hydronium and hydroxide ions:
\[ \ce{ 2 H_2O (l) \rightleftharpoons H_3O^+ (aq) + OH^{−} (aq)} \label{1}\]
This is also called the self-ionization of water. The concentration of \(H_3O^+\) and \(OH^-\) are equal in pure water because of the 1:1 stoichiometric ratio of Equation \(\ref{1}\). The molarity of H3O+ and OH- in water are also both \(1.0 \times 10^{-7} \,M\) at 25° C. Therefore, a constant of water (\(K_w\)) is created to show the equilibrium condition for the self-ionization of water. The product of the molarity of hydronium and hydroxide ion is always \(1.0 \times 10^{-14}\) (at room temperature).
\[K_w= [H_3O^+][OH^-] = 1.0 \times 10^{-14} \label{2}\]
Equation \(\ref{2}\) also applies to all aqueous solutions. However, \(K_w\) does change at different temperatures, which affects the pH range discussed below.
\(H^+\) and \(H_3O^+\) is often used interchangeably to represent the hydrated proton, commonly call the hydronium ion.
Equation \ref{1} can also be written as
\[ H_2O \rightleftharpoons H^+ + OH^- \label{3}\]
As expected for any equilibrium, the reaction can be shifted to the reactants or products:
- If an acid (\(H^+\)) is added to the water, the equilibrium shifts to the left and the \(OH^-\) ion concentration decreases
- If base ( \(OH^-\)) is added to water, the equilibrium shifts to left and the \(H^+\) concentration decreases.
pH and pOH
Because the constant of water, Kw is \(1.0 \times 10^{-14}\) (at 25° C), the \(pK_w\) is 14, the constant of water determines the range of the pH scale. To understand what the pKw is, it is important to understand first what the "p" means in pOH and pH. The addition of the "p" reflects the negative of the logarithm, \(-\log\). Therefore, the pH is the negative logarithm of the molarity of H, the pOH is the negative logarithm of the molarity of \(\ce{OH^-}\), and the \(pK_w\) is the negative logarithm of the constant of water:
\[ \begin{align} pH &= -\log [H^+] \label{4a} \\[4pt] pOH &= -\log [OH^-] \label{4b} \\[4pt] pK_w &= -\log [K_w] \label{4c} \end{align}\]
At room temperature,
\[K_w =1.0 \times 10^{-14} \label{4d}\]
So
\[\begin{align} pK_w &=-\log [1.0 \times 10^{-14}] \label{4e} \\[4pt] &=14 \end{align}\]
Using the properties of logarithms, Equation \(\ref{4e}\) can be rewritten as
\[10^{-pK_w}=10^{-14}. \label{4f}\]
The equation also shows that each increasing unit on the scale decreases by the factor of ten on the concentration of \(\ce{H^{+}}\). Combining Equations \ref{4a} - \ref{4c} and \ref{4e} results in this important relationship:
\[pK_w= pH + pOH = 14 \label{5b}\]
Equation \ref{5b} is correct only at room temperature since changing the temperature will change \(K_w\).
The pH scale is logarithmic, meaning that an increase or decrease of an integer value changes the concentration by a tenfold. For example, a pH of 3 is ten times more acidic than a pH of 4. Likewise, a pH of 3 is one hundred times more acidic than a pH of 5. Similarly a pH of 11 is ten times more basic than a pH of 10.
From the simple definition of pH in Equation \ref{4a}, the following properties can be identified:
- This scale is convenient to use, because it converts some odd expressions such as \(1.23 \times 10^{-4}\) into a single number of 3.91.
- This scale covers a very large range of \(\ce{[H+]}\), from 0.1 to 10-14. When \(\ce{[H+]}\) is high, we usually do not use the pH value, but simply the \(\ce{[H+]}\). For example, when \(\mathrm{[H^+] = 1.0}\), pH = 0. We seldom say the pH is 0, and that is why you consider pH = 0 such an odd expression. A pH = -0.30 is equivalent to a \(\ce{[H+]}\) of 2.0 M. Negative pH values are only for academic exercises. Using the concentrations directly conveys a better sense than the pH scales.
- The pH scale expands the division between zero and 1 in a linear scale or a compact scale into a large scale for comparison purposes. In mathematics, you learned that there are infinite values between 0 and 1, or between 0 and 0.1, or between 0 and 0.01 or between 0 and any small value. Using a log scale certainly converts infinite small quantities into infinite large quantities.
- The non-linearity of the pH scale in terms of \(\ce{[H+]}\) is easily illustrated by looking at the corresponding values for pH between 0.1 and 0.9 as follows:
| pH | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|---|---|---|---|
| [H+] | 1 | 0.79 | 0.63 | 0.50 | 0.40 | 0.32 | 0.25 | 0.20 | 0.16 | 0.13 |
- Because the negative log of \(\ce{[H+]}\) is used in the pH scale, the pH scale usually has positive values. Furthermore, the larger the pH, the smaller the \(\ce{[H+]}\).
The Effective Range of the pH Scale
It is common that the pH scale is argued to range from 0-14 or perhaps 1-14, but neither is correct. The pH range does not have an upper nor lower bound, since as defined above, the pH is an indication of concentration of H+. For example, at a pH of zero the hydronium ion concentration is one molar, while at pH 14 the hydroxide ion concentration is one molar. Typically the concentrations of H+ in water in most solutions fall between a range of 1 M (pH=0) and 10-14 M (pH=14). Hence a range of 0 to 14 provides sensible (but not absolute) "bookends" for the scale. One can go somewhat below zero and somewhat above 14 in water, because the concentrations of hydronium ions or hydroxide ions can exceed one molar. Figure \(\PageIndex{1}\) depicts the pH scale with common solutions and where they are on the scale.
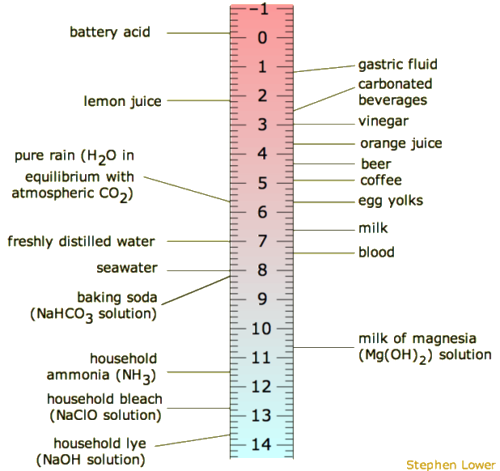
- If pH >7, the solution is basic. The pOH should be looked in the perspective of OH- instead of H+. Whenever the value of pOH is less than 7, then it is considered basic. And therefore there are more OH- than H+ in the solution.
- At pH 7, the substance or solution is at neutral and means that the concentration of H+ and OH- ion is the same.
- If pH < 7, the solution is acidic. There are more H+ than OH- in an acidic solution.
- The pH scale does not have an upper nor lower bound.
If the concentration of \(NaOH\) in a solution is \(2.5 \times 10^{-4}\; M\), what is the concentration of \(H_3O^+\)?
Solution
We can assume room temperature, so
\[1.0 \times 10^{-14} = [H_3O^+][OH^-] \nonumber\]
to find the concentration of H3O+, solve for the [H3O+].
\[\dfrac{1.0 \times 10^{-14}}{[OH^-]} = [H_3O^+]\]
\[\dfrac{1.0 \times 10^{-14}}{2.5 \times 10^{-4}} = [H_3O^+] = 4.0 \times 10^{-11}\; M\]
- Find the pH of a solution of 0.002 M of HCl.
- Find the pH of a solution of 0.00005 M NaOH.
Solution
- The equation for pH is -log [H+]
\[[H^+]= 2.0 \times 10^{-3}\; M \nonumber\]
\[pH = -\log [2.0 \times 10^{-3}] = 2.70 \nonumber\]
- The equation for pOH is -log [OH-]
\[ [OH^-]= 5.0 \times 10^{-5}\; M \nonumber\]
\[pOH = -\log [5.0 \times 10^{-5}] = 4.30 \nonumber\]
\[pK_w = pH + pOH \nonumber\]
and
\[pH = pK_w - pOH \nonumber\]
then
\[pH = 14 - 4.30 = 9.70 \nonumber\]
If moist soil has a pH of 7.84, what is the H+ concentration of the soil solution?
Solution
\[pH = -\log [H^+] \nonumber\]
\[7.84 = -\log [H^+] \nonumber\]
\[[H^+] = 1.45 \times 10^{-8} M \nonumber\]
Hint
Place -7.84 in your calculator and take the antilog (often inverse log or 10x) = 1.45 x 10-8M
Proper Definition of pH
The pH scale was originally introduced by the Danish biochemist S.P.L. Sørenson in 1909 using the symbol pH. The letter p is derived from the German word potenz meaning power or exponent of, in this case, 10. In 1909, S.P.L. Sørenson published a paper in Biochem Z in which he discussed the effect of H+ ions on the activity of enzymes. In the paper, he invented the term pH (purported to mean pondus hydrogenii in Latin) to describe this effect and defined it as the \(-\log[H^+]\). In 1924, Sørenson realized that the pH of a solution is a function of the "activity" of the H+ ion and not the concentration. Thus, he published a second paper on the subject. A better definition would be
\[pH = -\log\,a\{\ce{H^{+}}\}\]
where \(a\{H^+\}\) denotes the activity (an effective concentration) of the H+ ions. The activity of an ion is a function of many variables of which concentration is one.
- Concentration is abbreviated by using square brackets, e.g., \([H_3O^+]\) is the concentration of hydronium ion in solution.
- Activity is abbreviated by using "a" with curly brackets, e.g., \(a\{H_3O^+\}\) is the activity of hydronium ions in solution
Because of the difficulty in accurately measuring the activity of the \(\ce{H^{+}}\) ion for most solutions the International Union of Pure and Applied Chemistry (IUPAC) and the National Bureau of Standards (NBS) has defined pH as the reading on a pH meter that has been standardized against standard buffers. The following equation is used to calculate the pH of all solutions:
\[\begin{align} pH &= \dfrac{F(E-E_{standard})}{RT\;\ln 10} + pH_{standard} \label{6a} \\[4pt] &= \dfrac{5039.879 (E-E_{standard})}{T} + pH_{standard} \label{6b} \end{align}\]
with
- \(R\) is the ideal gas constant,
- \(F\) is the Faraday's constant, and
- \(T\) is absolute temperature (in K)
The activity of the H+ ion is determined as accurately as possible for the standard solutions used. The identity of these solutions vary from one authority to another, but all give the same values of pH to ± 0.005 pH unit. The historical definition of pH is correct for those solutions that are so dilute and so pure the H+ ions are not influenced by anything but the solvent molecules (usually water).
When measuring pH, [H+] is in units of moles of H+ per liter of solution. This is a reasonably accurate definition at low concentrations (the dilute limit) of H+. At very high concentrations (10 M hydrochloric acid or sodium hydroxide, for example,) a significant fraction of the ions will be associated into neutral pairs such as H+Cl–, thus reducing the concentration of “available” ions to a smaller value which we will call the effective concentration. It is the effective concentration of H+ and OH– that determines the pH and pOH. The pH scale as shown above is called sometimes "concentration pH scale" as opposed to the "thermodynamic pH scale". The main difference between both scales is that in thermodynamic pH scale one is interested not in H+concentration, but in H+activity. What a person measures in the solution is just activity, not the concentration. Thus it is thermodynamic pH scale that describes real solutions, not the concentration one.
For solutions in which ion concentrations don't exceed 0.1 M, the formulas pH = –log [H+] and pOH = –log[OH–] are generally reliable, but don't expect a 10.0 M solution of a strong acid to have a pH of exactly –1.00! However, this definition is only an approximation (albeit very good under most situations) of the proper definition of pH, which depends on the activity of the hydrogen ion:
\[pH= -\log a\{H^+\} \approx -\log [H^+] \label{7}\]
The activity is a measure of the "effective concentration" of a substance, is often related to the true concentration via an activity coefficient, \(\gamma\):
\[a{H^+}=\gamma [H^+] \label{8}\]
Calculating the activity coefficient requires detailed theories of how charged species interact in solution at high concentrations (e.g., the Debye-Hückel Theory). In most solutions the pH differs from the -log[H+ ] in the first decimal point. The following table gives experimentally determined pH values for a series of HCl solutions of increasing concentration at 25 °C.
| Molar Concentration of \(HCl\) | pH defined as Concentration | Experimentally Determined pH | Relative Deviation |
|---|---|---|---|
| 0.00050 | 3.30 | 3.31 | 0.3% |
| 0.0100 | 2 | 2.04 | 1.9% |
| 0.100 | 1 | 1.10 | 9% |
| 0.40 | 0.39 | 0.52 | 25% |
| 7.6 | -0.88 | -1.85 | 52% |
While the pH scale formally measures the activity of hydrogen ions in a substance or solution, it is typically approximated as the concentration of hydrogen ions; this approximation is applicable only under low concentrations.
Living Systems
Molecules that make up or are produced by living organisms usually function within a narrow pH range (near neutral) and a narrow temperature range (body temperature). Many biological solutions, such as blood, have a pH near neutral. pH influences the structure and the function of many enzymes (protein catalysts) in living systems. Many of these enzymes have narrow ranges of pH activity. Cellular pH is so important that death may occur within hours if a person becomes acidotic (having increased acidity in the blood). As one can see pH is critical to life, biochemistry, and important chemical reactions. Common examples of how pH plays a very important role in our daily lives are given below:
- Water in swimming pool is maintained by checking its pH. Acidic or basic chemicals can be added if the water becomes too acidic or too basic.
- Whenever we get a heartburn, more acid build up in the stomach and causes pain. We needs to take antacid tablets (a base) to neutralize excess acid in the stomach.
- The pH of blood is slightly basic. A fluctuation in the pH of the blood can cause in serious harm to vital organs in the body.
- Certain diseases are diagnosed only by checking the pH of blood and urine.
- Certain crops thrive better at certain pH range.
- Enzymes activate at a certain pH in our body.
| Compartment | pH |
|---|---|
| Gastric Acid | 1 |
| Lysosomes | 4.5 |
| Granules of Chromaffin Cells | 5.5 |
| Human Skin | 5.5 |
| Urine | 6 |
| Neutral H2O at 37 °C | 6.81 |
| Cytosol | 7.2 |
| Cerebrospinal Fluid | 7.3 |
| Blood | 7.43-7.45 |
| Mitochondrial Matrix | 7.5 |
| Pancreas Secretions | 8.1 |
Problems
- In a solution of \(2.4 \times 10^{-3} M\) of HI, find the concentration of \(OH^-\).
- Determine the pH of a solution that is 0.0035 M HCl.
- Determine the [H3O+] of a solution with a pH = 5.65
- If the pOH of NH3, ammonia, in water is 4.74. What is the pH?
- Pepsin, a digestive enzyme in our stomach, has a pH of 1.5. Find the concentration of OH- in the stomach.
Solutions
- We use the dissociation of water equation to find [OH-].
Kw = [H3O+][OH-] = 1.0 X 10-14
Solve for [OH-]
[OH-] = (1.0 X 10-14)/ [H3O+]
Plug in the molarity of HI and solve for OH-.
[OH-] = (1.0 X 10-14)/ [2.4 X 10-3] = 4.17 X 10-12 M. - pH = -log[H3O+]
Plug the molarity of the HCl in and solve for pH.
pH = -log[0.0035] = 2.46 - pH = -log[H3O+]
Plug in the pH and solve for [H3O+]
5.65 = -log[H3O+]
Move the negative sign to the pH. -5.65 = log[H3O+]
10-5.65=10log[H3O+] = 2.24 X 10-6 M - pH + pOH = 14
Solve for pH.
14 - pOH = pH
14 - 4.74 = pH = 9.26 - There are several ways to do this problem.
Answer 1.
pH + pOH = 14
Solve for pOH.
pOH = 14 - pH
pOH = 14 - 1.5 = 12.5
When the pOH is solved, solve for the concentration by using log.
pOH = -log[OH-]
12.5 = -log[OH-]
-12.5 = log[OH-]
10-12.5 = 10log[OH-] = 3.16 X 10-13 M.
Answer 2.
pH = -log[H+]
Plug in the pH and solve for the molarity of H+ of pepsin.
1.5 = -log[H+]
-1.5 = log[H+]
10-1.5 = 10log[H+] = [H+]= 0.032
Use the concentration of H+ to solve for the concentration of OH-.
[H+][OH-] = 1.0 X 10-14
Plug in the [H+] and solve for [OH-].
[OH-] = (1.0 X 10-14)/[H3O+]
[OH-] = (1.0 X 10-14)/(0.032) = 3.125 X 10-14 M
References
- Petrucci, et al. "Self-Ionization of Water and the pH Scale." General Chemistry: Principles & Modern Applications. 7th ed. Upper Saddle River: Pearson Prentice Hall, 2007. 669-71.
- Segel, Irwin H. "Acid and Base." Biochemical Calculations. 2nd ed. Wiley: BK Book, 1976. 12.
- Christopher G. McCarty and Ed Vitz, Journal of Chemical Education, 83(5), 752 (2006)
Contributors and Attributions
- Emmellin Tung (UCD), Sharon Tsao (UCD), Divya Singh (UCD), Patrick Gormley (Lapeer Community School District)
Chung (Peter) Chieh (Professor Emeritus, Chemistry @ University of Waterloo)

