10.30: The Variation Method in Momentum Space
- Page ID
- 136979
The following normalized trial wavefunction is proposed for a variational calculation on the harmonic oscillator.
\[ \psi (x, a) := \sqrt{ \frac{1}{a}} exp( \frac{-|x|}{a}) \nonumber \]
\[ \int_{- \infty}^{ \infty} \psi (x, a)^2 dx~~~assume,~a > 0 \rightarrow 1 \nonumber \]
However, the graph below shows a cusp at x = 0, indicating that the wavefunction is not well‐behaved and therefore cannot be used for quantum mechanical calculations.
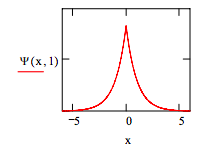
Therefore, the wavefunction is Fourier transformed into the momentum representation.
\[ \Phi (p, a) := \int_{- \infty}^{ \infty} \frac{exp(-ipx)}{ \sqrt{2 \pi}} \sqrt{ \frac{1}{a}} exp( \frac{-|x|}{a}) dx~|_{simplify}^{assume,~a>0} \rightarrow (-a^{ \frac{1}{2}}) \frac{2^{ \frac{1}{2}}}{(ipa-1) \pi ^{ \frac{1}{2}} (ipa +1)} \nonumber \]
Normalization is checked and the function is graphed.
\[ \int_{- \infty}^{ \infty} \Phi (p, a)^2 dp~~~assume,~a > 0 \rightarrow 1 \nonumber \]
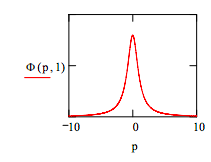
The momentum wavefunction appears to be well‐behaved, so a variational calculation will be carried out in momentum space.
Assuming a m = k =1 and h = 2π, we have for the harmonic oscillator in momentum space.
- Momentum space integral: \( \int_{- \infty}^{ \infty} \blacksquare dp\)
- Momentum operator: \( p \blacksquare\)
- Kinetic energy operator: \( \frac{p^2}{2}\)
- Position operator: \( i \frac{d}{dp} \blacksquare\)
- Potential energy operator: \( \frac{-1}{2} \frac{d^2}{dp^2} \blacksquare\)
Evaluate the energy integral in the momentum representation:
\[ E(a) := \int_{- \infty}^{ \infty} \Phi (p, a) \frac{p^2}{2} \Phi (p, a) dp... + \int_{- \infty}^{ \infty} \Phi (p, a) \frac{-1}{2} \frac{d^2}{dp^2} \Phi (p, a) dp~|_{assume,~a >0}^{simplify} \rightarrow \frac{1}{4} \frac{2 + a^4}{a^2} \nonumber \]
Minimize energy with respect to the variational parameter:
a := 1 a := Minimize (E, a) a = 1.189 E(a) = 0.707
Display optimum wavefunction along with exact wavefunction:
\[ Exact(p) := \frac{1}{ \pi ^{ \frac{1}{4}}} e^{ \frac{-1}{2} p^2} \nonumber \]
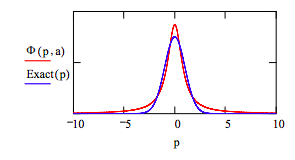
Naturally the agreement with the exact solution is not favorable because of the poor quality of the original coordinate space wavefunction.
\[ \frac{E(a) - 0.5}{0.5} = 41.421 \nonumber \]

