8.86: Simulating a Quantum Computer with a Mach-Zehnder Interferometer

Suppose you are asked if two pieces of glass are the same thickness. The convential thing to do is to measure the thickness of each piece of glass and then compare the results. As David Deutsch pointed out this is overkill. You were asked only if they were the same thickness, but you made two measurements to answer that question, when in fact it can be done with one.

Quantum mechanics provides two ways to answer the question; using a double-slit apparatus or a Mach-Zehnder interferometer. They both operate on the same quantum principles. Using the double-slit apparatus you put a piece of glass behind each of the slits and shine light on the slits. If the resulting diffraction pattern is symmetrical about the center of the slits, the glasses are the same thickness. See the previous tutorial: Simulating the Deutsch-Jozsa Algorithm with a Double-Slit Apparatus.

Alternatively you could put a piece of glass in each arm of an equal-arm Mach-Zehnder interferometer (MZI). How this approach works is the subject of this tutorial. First we need to get acquainted with a MZI.

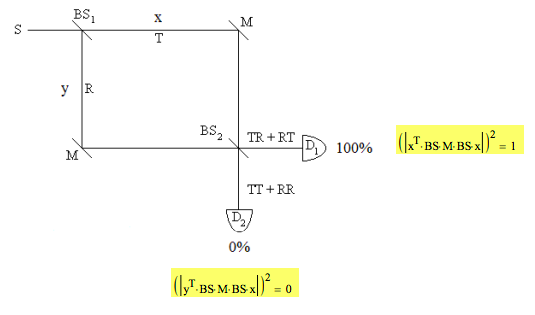
As shown in the following figure a MZI consists of a photon source, two 50-50 beam splitters, two mirrors and two detectors. The Appendix contains the mathematical information necessary to carry out a matrix mechanics analysis of the operation of the interferometer. The motional states of the photon are represented by vectors, while the beam splitters and mirrors are represented by matrices and operate on the vectors.

Yogi Berra has famously said "When you come to a fork in the road, take it." This is exactly what the photon does at a beam splitter. After the first beam splitter the photon, which was moving in the x-direction being emitted by the source, is now in a superposition of moving in both the x- and y-directions. It has been transmitted and reflected at the beam splitter. By convention a 90 degree (π/2, i) phase shift is assigned to reflection.

The following calculations illustrate the formation of the superposition state created by the photon's interaction with the first beam splitter.

\[ \begin{matrix} \text{BS x} \rightarrow \begin{pmatrix} \frac{ \sqrt{2}}{2} \\ \frac{ \sqrt{2} i}{2} \end{pmatrix} & S = \frac{1}{ \sqrt{2}} (T + iR) & \frac{1}{ \sqrt{2}} x + \frac{i}{ \sqrt{2}}y \rightarrow \begin{pmatrix} \frac{ \sqrt{2}}{2} \\ \frac{ \sqrt{2} i}{2} \end{pmatrix} \end{matrix} \nonumber \]

After the initial beam splitter, the mirrors direct the transmitted and reflected photon states to a second beam splitter where they are recombined. The consequence of this in an equal arm MZI is that the photon is alway registered at D₁. There are two paths (histories) to each detector and the amplitudes for these paths interfere. To reach D₁ both paths experience one reflection and so arrive in phase with each other with their phases shifted by 90 degrees. The paths to D₂, however, are 180 degrees out of phase and destructively interfere. The photon is never detected at D₂.

A photon entering the MZI in the x-direction exits in the x-direction phase-shifted by 90 degrees:

\[ \begin{matrix} \text{BS M BS x} \rightarrow \begin{pmatrix} i \\ 0 \end{pmatrix} & \text{i x} \rightarrow \begin{pmatrix} i \\ 0 \end{pmatrix} \end{matrix} \nonumber \]

The highlighted areas above next to the detectors show the matrix mechanics calculations for the probability of the photon being registered at D₁ and D₂. The equations are read from the right. A photon moving in the x-direction interacts with a beam splitter, a mirror and another beam splitter. This state is then projected onto x- and y-direction motion to calculate which detector will register the photon. The absolute square of this calculation (the probability amplitude) is the probability.

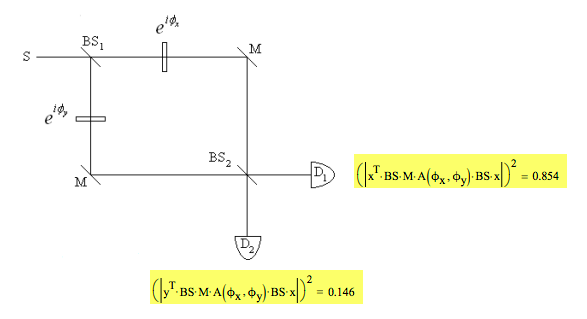
Now we place the pieces of glass in the arms of the interferometer as shown below. The speed of light in glass is different from that in air. Therefore glass causes a phase shift depending on its thickness as is shown below. If the pieces of glass are the same thickness, δ, they will cause the same phase shift and the photon will be detected at D₁. However, if they have different thicknesses, the phase shifts will be different in the two arms of the interferometer. For example, if ϕx is π/2 and ϕy is π/4 then D₂ will fire almost 15% of the time indicating that the glasses are not the same thickness.

\[ \begin{matrix} \phi_x = 2 \pi \frac{ \delta_x}{ \lambda} & \phi_x = \frac{ \pi}{2} & \phi_y 2 \pi \frac{ \delta_y}{ \lambda} & \phi_y = \frac{ \pi}{4} \end{matrix} \nonumber \]

Appendix

State Vectors

\[ \begin{matrix} \text{Photon moving horizontally:} & x = \begin{pmatrix} 1 \\ 0 \end{pmatrix} & \text{Photon moving vertically:} & y = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \end{matrix} \nonumber \]

Operators

\[ \begin{matrix} \text{Operator representing a beam splitter:} & \text{BS} = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 & i \\ i & 1 \end{pmatrix} \\ \text{Operator representing interaction with glass:} & \text{A} \left( \phi_x,~ \phi_y \right) = \begin{pmatrix} e^{i \phi_x} & 0 \\ 0 & e^{i \phi_y} \end{pmatrix} \\ \text{Operator representing a mirror:} & \text{M} = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \end{matrix} \nonumber \]