7.32: Two Photon Entanglement - A Tensor Algebra Analysis
- Page ID
- 142301
Photons from separate sources, u and d, arrive simultaneously at the beam splitter shown in the figure below.
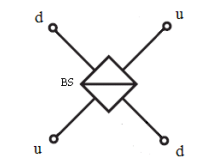
Because the photons arrive simultaneously at the beam splitter they are indistinguishable and donʹt possess separate identities. We are forced by quantum mechanical principles to represent their collective state at the beam splitter (BS) by the following entangled wave function. The plus sign in this superposition indicates that photons are bosons; their wave functions are symmetric with respect to the interchange of the photon labels.
\[ | \Psi_B \rangle = \frac{1}{ \sqrt{2}} \left[ | u \rangle_1 |d \rangle_2 + |d \rangle_1 |u \rangle_2 \right] \nonumber \]
The following vector representations are used for the photon motional states.
\[ |u \rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \nonumber \]
\[ |d \rangle = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \nonumber \]
Writing \( \Psi_B\) in tensor format yields,
\[ | \Psi _B\rangle = \frac{1}{ \sqrt{2}} \left[ \begin{pmatrix} 1 \\ 0 \end{pmatrix} \otimes \begin{pmatrix} 0 \\ 1 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 1 \\ 0 \end{pmatrix} \right] = \frac{1}{ \sqrt{2}} \left[ \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix} \right] = \frac{1}{ \sqrt{2}} \begin{pmatrix} 0 \\ 1 \\ 1 \\ 0 \end{pmatrix} \nonumber \]
\[ \Psi _B = \frac{1}{ \sqrt{2}} \begin{pmatrix} 0 \\ 1 \\ 1 \\ 0 \end{pmatrix} \nonumber \]
Transmission and reflection occur at 50-50 beam splitters. By convention, reflection is assigned a π/2 (exp(iπ/2) = i) phase shift relative to transmission. The matrix representing a 50-50 beam splitter operating on an individual photon is given below, along with its effect on the u and d photon states.
\[ BS = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 & i \\ i & 1 \end{pmatrix} \nonumber \]
\[ BS \begin{pmatrix} 1 \\ 0 \end{pmatrix} \rightarrow \begin{pmatrix} \frac{ \sqrt{2}}{2} \\ \frac{ \sqrt{2} i}{2} \end{pmatrix} \nonumber \]
\[ BS \begin{pmatrix} 0 \\ 1 \end{pmatrix} \rightarrow \begin{pmatrix} \frac{ \sqrt{2}i }{2} \\ \frac{ \sqrt{2}}{2} \end{pmatrix} \nonumber \]
This shows that the beam splitter converts pure states, u and d, into superpositions of u and d.
In this experiment the beam splitter operates on both photons, so in tensor format the operator representing the beam splitter becomes the following 4x4 matrix.
\[ \hat{BS} = \hat{BS}_2 \otimes \hat{BS}_1 = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 & i \\ i & 1 \end{pmatrix} \otimes \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 & i \\ i & 1 \end{pmatrix} \frac{1}{2} \begin{pmatrix} 1 \begin{pmatrix} 1 & i \\ i & 1 \end{pmatrix} & i \begin{pmatrix} 1 & i \\ i & 1 \end{pmatrix} \\ i \begin{pmatrix} 1 & i \\ i & 1 \end{pmatrix} & 1 \begin{pmatrix} 1 & i \\ i & 1 \end{pmatrix} \end{pmatrix} = \frac{1}{2} \begin{pmatrix} 1 & i & i & -1 \\ i & 1 & -1 & i \\ i & -1 & 1 & i \\ -1 & i & i & 1 \end{pmatrix} \nonumber \]
There are four possible photon output states after the beam splitter (|uu >, |ud >, |du >, |dd >), which are shown below in tensor format.
\[ |uu \rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \otimes \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} \nonumber \]
\[ uu = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} \nonumber \]
\[ |ud \rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \otimes \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} \nonumber \]
\[ ud = \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} \nonumber \]
\[ |du \rangle = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix} \nonumber \]
\[ du = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix} \nonumber \]
\[ |dd \rangle = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix} \nonumber \]
\[ dd = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix} \nonumber \]
The output state created by the interaction of the initial entangled state with the beam splitter is,
\[ \Psi_{Bout} = \frac{1}{2} \begin{pmatrix} 1 & i & i & -1 \\ i & 1 & -1 & i \\ i & -1 & 1 & i \\ -1 & i & i & 1 \end{pmatrix} \frac{1}{ \sqrt{2}} \begin{pmatrix} 0 \\ 1 \\ 1 \\ 0 \end{pmatrix} \rightarrow \begin{pmatrix} \frac{ \sqrt{2} i}{2} \\ 0 \\ 0 \\ \frac{ \sqrt{2} i}{2} \end{pmatrix} \nonumber \]
By inspection we can see that the photons are always observed in the same output channel, either |uu > or |dd >, with equal probabilities of 0.5 (|0.707i|2). Not surprisingly we see bosonic behavior by the photons. After the beam splitter they are in an even superposition of both being at u and both being at d. Unlike fermions bosons can be in the same state at the same time.
\[ \left( \left| uu^T \Psi _{Bout} \right| \right)^2 \rightarrow \frac{1}{2} \nonumber \]
\[ \left( \left| dd^T \Psi _{Bout} \right| \right)^2 \rightarrow \frac{1}{2} \nonumber \]
Naturally this means they are never observed in different output channels, |ud> or |du>.
\[ \left( \left| ud^T \Psi _{Bout} \right| \right)^2 \rightarrow 0 \nonumber \]
\[ \left( \left| du^T \Psi _{Bout} \right| \right)^2 \rightarrow 0 \nonumber \]
Now letʹs pretend that photons are fermions and examine the consequences for this experiment. Fermions have antisymmetric wave functions; the wave function changes sign on interchange of the constituents labels.
\[ | \Psi _F \rangle = \frac{1}{ \sqrt{2}} \left[ |u \rangle_1 |d \rangle_2 - |d \rangle_1 |u \rangle_2 \right] \nonumber \]
Written in tensor format the antisymmetric wave function is
\[ | \Psi_F \rangle = \frac{1}{ \sqrt{2}} \left[ \begin{pmatrix} 1 \\ 0 \end{pmatrix} \otimes \begin{pmatrix} 0 \\ 1 \end{pmatrix} - \begin{pmatrix} 0 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 1 \\ 0 \end{pmatrix} \right] = frac{1}{ \sqrt{2}} \left[ \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix} \right] = \frac{1}{ \sqrt{2}} \begin{pmatrix} 0 \\ 1 \\ -1 \\ 0 \end{pmatrix} \nonumber \]
\[ \Psi _F = \frac{1}{ \sqrt{2}} \begin{pmatrix} 0 \\ 1 \\ -1 \\ 0 \end{pmatrix} \nonumber \]
Now the interaction with the beam splitter yields the following result.
\[ |Psi _{Fout} = \frac{1}{2} \begin{pmatrix} 1 & i & i & 1 \\ i & 1 & -1 & i \\ i & -1 & 1 & i \\ -1 & i & i & 1 \end{pmatrix} \frac{1}{ \sqrt{2}} \begin{pmatrix} 0 \\ 1 \\ -1 \\ 0 \end{pmatrix} \rightarrow \begin{pmatrix} 0 \\ \frac{ \sqrt{2}}{2} \\ - \frac{ \sqrt{2}}{2} \\ 0 \end{pmatrix} \nonumber \]
We see by inspection or calculation that fermionic photons are never observed in the same output channel after interaction with the beam splitter.
\[ \left( \left| uu^T \Psi_{Fout} \right| \right)^2 \rightarrow 0 \nonumber \]
\[ \left( \left| dd^T \Psi_{Fout} \right| \right)^2 \rightarrow 0 \nonumber \]
Naturally this means they are always observed in different output channels, |ud > or |du>.
\[ \left( \left| ud^T \Psi_{Fout} \right| \right)^2 \rightarrow \frac{1}{2} \nonumber \]
\[ \left( \left| du^T \Psi_{Fout} \right| \right)^2 \rightarrow \frac{1}{2} \nonumber \]
In summary, the sociology of bosons and fermions can be briefly stated: bosons are gregarious and enjoy company; fermions are antisocial and prefer solitude.

