7.16: Matrix Mechanics Exercises Using Polarized Light
- Page ID
- 141576
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Eigenstates and operators are provided for a series of matrix mechanics exercises involving polarized light.
Eigenstate for a \( \theta\)-polarized light:
\[ \Theta ( \theta) = \begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix} \nonumber \]
\[ \begin{pmatrix} \cos \theta & \sin \theta \end{pmatrix} \begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix} ~ simplify~ \rightarrow 1 \nonumber \]
\[ | \theta \rangle = \begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix} \nonumber \]
\[ \langle \theta | \theta \rangle = \begin{pmatrix} \cos \theta & \sin \theta \end{pmatrix} \begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix} = 1 \nonumber \]
Operator for a \( \theta\)-oriented polarizer:
\[ \Theta_{op} ( \theta) = \begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix}\begin{pmatrix} \cos \theta & \sin \theta \end{pmatrix} \rightarrow \begin{pmatrix} \cos \theta^2 & \cos \theta \sin \theta \\ \cos \theta & \sin \theta^2 \end{pmatrix} \nonumber \]
\[ \hat{ \Theta} | \theta \rangle \langle \theta | = \begin{pmatrix} \cos \theta \\ \hline \sin \theta \end{pmatrix} \begin{pmatrix} \cos \theta & \sin \theta \end{pmatrix} \nonumber \]
Eigenstates for vertically, horizontally, and diagonally polarized light:
Vertically:
\[ V = \Theta (0) \rightarrow \begin{pmatrix} 1 \\ 0 \end{pmatrix} \nonumber \]
\[ V^T \rightarrow \begin{pmatrix} 1 & 0 \end{pmatrix} \nonumber \]
\[ |V \rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix} ~~ \langle V | = \begin{pmatrix} 1 & 0 \end{pmatrix} \nonumber \]
Horizontally:
\[ H = \Theta \left( \frac{ \pi}{2} \right) \rightarrow \begin{pmatrix} 0 \\ 1 \end{pmatrix} \nonumber \]
\[ H^T \rightarrow \begin{pmatrix} 0 & 1 \end{pmatrix} \nonumber \]
\[ |H \rangle = \begin{pmatrix} 0 \\ 1 \end{pmatrix} ~~ \langle H | = \begin{pmatrix} 0 & 1 \end{pmatrix} \nonumber \]
Diagonally:
\[ D = \Theta \left( \frac{ \pi}{4} \right) ~float,~4~ \rightarrow \begin{pmatrix} 0.7071 \\ 0.7071 \end{pmatrix} \nonumber \]
\[ D^T \rightarrow \begin{pmatrix} 0.7071 & 0.7071 \end{pmatrix} \nonumber \]
\[ |D \rangle = \begin{pmatrix} 0.707 \\ 0.707 \end{pmatrix} ~~ \langle D | = \begin{pmatrix} 0.707 & 0.707 \end{pmatrix} \nonumber \]
Operators for vertically, horizontally, and diagonally oriented polarizers:
Vertically:
\[ V_{op} = \Theta _{op} (0) \rightarrow \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix} \nonumber \]
\[ \hat{V} = |V \rangle \langle V| \nonumber \]
Horizontally:
\[ H_{op} = \Theta _{op} \left( \frac{ \pi}{2} \right) \rightarrow \begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix} \nonumber \]
\[ \hat{H} = |H \rangle \langle H| \nonumber \]
Diagonally:
\[ D_{op} = \Theta _{op} \left( \frac{ \pi}{4} \right) ~ float,~1~ \rightarrow \begin{pmatrix} 0.5 & 0.5 \\ 0.5 & 0.5 \end{pmatrix} \nonumber \]
\[ \hat{D} = |D \rangle \langle D| \nonumber \]
Demonstrate that a \( \theta\)‐polarized photon is an eigenfunction of a \( \theta\)‐oriented polarizer, with eigenvalue 1.
\[ \begin{pmatrix} \cos \theta^2 & \cos \theta \sin \theta \\ \cos \theta \sin \theta & \sin \theta^2 \end{pmatrix} \begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix} ~simplify \rightarrow \begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix} \nonumber \]
\[ \hat{ \Theta} | \theta \rangle = | \theta \rangle \nonumber \]
or
\[ \Theta_{op} ( \theta) \Theta ( \theta) simplify~ \rightarrow \begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix} \nonumber \]
Demonstrate that a \( \theta\)‐polarized photon is a linear superposition of the vertical and horizontal polarization states.
\[ \cos \theta \begin{pmatrix} 1 \\ 0 \end{pmatrix} + \sin \theta \begin{pmatrix} 0 \\ 1 \end{pmatrix} \rightarrow \begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix} \nonumber \]
Demonstrate that a vertically polarized photon is a linear superposition of the \( \pi\)/4 and -\( \pi\)/4 polarization states.
\[ \frac{1}{ \sqrt{2}} \left[ \begin{pmatrix} \cos \frac{ \pi}{4} \\ \sin \frac{ \pi}{4} \end{pmatrix} + \begin{pmatrix} \cos \frac{ \pi}{4} \\ \sin \frac{- \pi}{4} \end{pmatrix} \right] \rightarrow \begin{pmatrix} 1 \\ 0 \end{pmatrix} \nonumber \]
Calculate the probability amplitude and probability that a \( \pi\)/3 (60 degree) polarized photon will pass a vertical polarizer.
\[ V^T \Theta \frac{ \pi}{3} = 0.5 \nonumber \]
\[ \left( \left| V^T \Theta \left( \frac{ \pi}{3} \right) \right| \right) = 0.25 \nonumber \]
or
\[ \Theta \left( \frac{ \pi}{3} \right)^T V_{op} \Theta \left( \frac{ \pi}{3} \right) = 0.25 \nonumber \]
\[ \left\langle V| \frac{ \pi}{3} \right\rangle = 0.5 \nonumber \]
\[ \left| \left\langle V| \frac{ \pi}{3} \right\rangle \right|^2 = 0.5 \nonumber \]
\[ \left\langle \frac{ \pi}{3} \left| \hat{V} \right| \frac{ \pi}{3} \right\rangle = \left\langle \frac{ \pi}{3} | V \right\rangle \left\langle V | \frac{ \pi}{3} \right\rangle = \left| \left\langle V | \frac{ \pi}{3} \right\rangle \right|^2 = 0.25 \nonumber \]
Calculate the probability amplitude and probability that vertically polarized photon will pass a \( \pi\)/3 (60 degree) polarizer.
\[ \Theta \left( \frac{ \pi}{3} \right) V = 0.5 \nonumber \]
\[ \left( \left| \Theta \left( \frac{ \pi}{3} \right)^T V \right| \right) ^2 = 0.25 \nonumber \]
or
\[ V^T \Theta_{op} \left( \frac{ \pi}{3} \right) V = 0.25 \nonumber \]
Calculate the probability amplitude and probability that a \( \pi\)/3 (60 degree) polarized photon will pass a diagonal polarizer.
\[ D^T \Theta \left( \frac{ \pi}{3} \right) = 0.966 \nonumber \]
\[ \left( \left| D^T \Theta \left( \frac{ \pi}{3} \right) \right| \right)^2 = 0.933 \nonumber \]
or
\[ \Theta \left( \frac{ \pi}{3} \right) D_{op} \Theta \left( \frac{ \pi}{3} \right) = 0.933 \nonumber \]
Calculate the probability that a \( \pi\)/3 (60 degree) polarized photon will pass the following sequence of polarizers: vertical, diagonal, horizontal.
\[ \left( \left| H^T H_{op} D_{op} V_{op} \Theta \left( \frac{ \pi}{3} \right) \right| \right)^2 = 0.063 \nonumber \]
\[ \left| \langle H | \hat{H} \hat{D} \hat{V} \left| \frac{ \pi}{3} \right\rangle \right|^2 = 0.063 \nonumber \]
Calculate the probability that a \( \pi\)/3 (60 degree) polarized photon will pass the following sequence of polarizers: vertical, horizontal, diagonal. Explain the result.
\[ \left( \left| D^T D_{op} H_{op} V_{op} \Theta \left( \frac{ \pi}{3} \right) \right| \right)^2 = 0 \nonumber \]
With this sequence the first two polarizers are crossed (have a 90 degree relative angle). Thus the vertically polarized photon emerging from the first polarizer is stopped by the second polarizer.
Confirm the results shown in the diagram shown below. In other words, show that 12.5% of the incident unpolarized light will pass an arrangement of vertical, diagonal and horizontal polarizers.
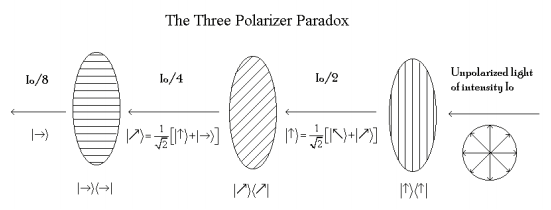
\[ \frac{2}{ \pi} \int_{0}^{ \frac{ \pi}{2}} \left( \left| H^T H_{op} D_{op} V_{op} \Theta ( \theta0 \right| \right)^2 d \theta = 0.125 \nonumber \]
\[ \frac{2}{ \pi} \int_{0}^{ \frac{ \pi}{2}} | \langle H | \hat{H} \hat{D} \hat{V} | \theta \rangle |^2 d \theta \nonumber \]
This calculation can also be performed assuming that unpolarized light is a 50‐50 mixture of vertically and horizontally polarized light.
\[ \frac{1}{2} ( | H^T H_{op} D_{op} V_{op} V |)^2 + \frac{1}{2} (| H^T H_{op} D_{op} V_{op} H |)^2 = 0.125 \nonumber \]
Now a \( \pi\)/6 polarizer is placed between the vertical and diagonal polarizers, and a \( \pi\)/3 polarizer is placed between the diagonal and horizontal polarizer. Calculate the fraction of light that emerges from the final horizontal polarizer and explain the result.
\[ \frac{2}{ \pi} \int_{0}^{ \frac{ \pi}{2}} \left( \left| H^T H_{op} \Theta_{op} \left( \frac{ \pi}{3} \right) D_{op} \Theta_{op} \left( \frac{ \pi}{6} \right) V_{op} \Theta ( \theta) \right| \right) ^2 d \theta = 0.245 \nonumber \]
This calculation can also be performed assuming that unpolarized light is a 50‐50 mixture of vertically and horizontally polarized light.
\[ \frac{1}{2} \left( \left| H^T H_{op} \Theta_{op} \left( \frac{ \pi}{3} \right) D_{op} \Theta_{op} \left( \frac{ \pi}{6} \right) V_{op} V \right| \right)^2 + \frac{1}{2} \left( \left| H^T H_{op} \Theta_{op} \left( \frac{ \pi}{3} \right) D_{op} \Theta_{op} \left( \frac{ \pi}{6} \right) V_{op} H \right| \right)^2 = 0.245 \nonumber \]
The initial and final polarizers are crossed and will not transmit light. A single p/4 polarizer sandwiched in between allows light through for the reasons presented earlier. The addition of two more polarizers increases the fraction of transmitted light because the relative angles between successive polarizers has been reduced. Significantly more light gets through each set of polarizers because the angle between them is smaller.
Calculate the probability that unpolarized light will pass the following sequence of polarizers: vertical, \( \pi\)/3 (60 degree), diagonal.
\[ \frac{2}{ \pi} \int_{0}^{ \frac{ \pi}{2}} \left( \left| D^T D_{op} \Theta_{op} \left( \frac{ \pi}{3} \right) V_{op} \Theta ( \theta) \right| \right) ^2 d \theta = 0.117 \nonumber \]
or
\[ \frac{2}{ \pi} \int_{0}^{ \frac{ \pi}{2}} \left( \left| D^T \Theta_{op} \left( \frac{ \pi}{3} \right) V_{op} \Theta ( \theta) \right| \right) ^2 d \theta = 0.117 \nonumber \]
Calculate the probability that unpolarized light will pass the following sequence of polarizers: vertical, diagonal, \( \pi\)/3 (60 degree). Explain the difference in the results.
\[ \frac{2}{ \pi} \int_{0}^{ \frac{ \pi}{2}} \left( \left| \Theta \left( \frac{ \pi}{3} \right)^T \Theta_{op} \left( \frac{ \pi}{3} \right) D_{op} V_{op} \Theta ( \theta) \right| \right) ^2 d \theta = 0.233 \nonumber \]
or
\[ \frac{2}{ \pi} \int_{0}^{ \frac{ \pi}{2}} \left( \left| \Theta \left( \frac{ \pi}{3} \right)^T D_{op} V_{op} \Theta ( \theta) \right| \right) ^2 d \theta = 0.233 \nonumber \]
The operators representing the measurement of diagonal and 60 degree polarization do not commute.
Calculate the polarization of the incident photon such that the probability it will pass three polarizers (vertical, horizontal, diagonal) is 0.10
\[ \theta = 75 ~deg \nonumber \]
Given
\[ \left( \left| H^T H_{op} D_{op} V_{op} \Theta ( \theta) \right| \right)^2 = .10 \nonumber \]
Find (\( \theta\)) = 50.768 deg
The next few exercises involve circularly polarized light.
The base states for circularly polarized light are:
\[ L = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ i \end{pmatrix} \nonumber \]
\[ R = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ -i \end{pmatrix} \nonumber \]
Show that they form an orthonormal basis set:
\[ \overline{L^T} L \rightarrow 1 \nonumber \]
\[ \overline{R^T} R \rightarrow 1 \nonumber \]
\[ \overline{L^T} R \rightarrow 0 \nonumber \]
\[ \overline{R^T} L \rightarrow 0 \nonumber \]
Show that they are linear superpositions of the vertical and horizontal polarization states:
\[ \frac{1}{ \sqrt{2}}\ (V + iH) = \begin{pmatrix} 0.707 \\ 0.707i \end{pmatrix}]
\[ \frac{1}{ \sqrt{2}}\ (V - iH) = \begin{pmatrix} 0.707 \\ -0.707i \end{pmatrix}]
Show that vertically and horizontally polarized light can be written as superpositions of circularly polarized light:
\[ \frac{1}{ \sqrt{2}}\ (L + R) = \begin{pmatrix} 1 \\ 0 \end{pmatrix}]
\[ \frac{i}{ \sqrt{2}}\ (R - L) = \begin{pmatrix} 0 \\ 1 \end{pmatrix}]
The angular momentum operator in atomic units is:
\[ Pang = \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix} \nonumber \]
Calculate the expectation value for angular momentum for a vertical, horizontal and diagonal polarized photon.
\[ V^T Pang (V) = 0 \nonumber \]
\[ H^T Pang (H) = 0 \nonumber \]
\[ D^T Pang (D) = 0 \nonumber \]
Calculate the expectation value for angular momentum for a \( \theta\) polarized photon.
\[ \Theta ( \theta)^T Pang \Theta ( \theta) = 0 \nonumber \]
Calculate the expectation value for angular momentum for left and right circularly polarized photons.
\[ \overline{L^T} Pang (L) = 1 \nonumber \]
\[ \overline{R^T} Pang (R) = -1 \nonumber \]
The remaining exercises deal with the effects of half and quarter wave plates.
The remaining exercises deal with the effects of half and quarter wave plates.
\[ W_2 = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \nonumber \]
\[ W_2 ( \theta) = \begin{pmatrix} \cos (2 \theta) & \sin (2 \theta) \\ \sin (2 \theta) & -\cos (2 \theta) \end{pmatrix} \nonumber \]
Quarter wave plate and \( \pi\)/4 rotated quarter wave plate (which has the same effect as a 50‐50 beam splitter):
\[ W_4 = \begin{pmatrix} 1 & 0 \\ 0 & -i \end{pmatrix} \nonumber \]
\[ BS = \begin{pmatrix} \frac{1}{ \sqrt{2}} & \frac{1}{ \sqrt{2}} \\ \frac{1}{ \sqrt{2}} & \frac{1}{ \sqrt{2}} \end{pmatrix} \nonumber \]
Show that,
When a half wave plate is placed between aligned polarizers all the light gets through.
\[ \left( \left| V^T W_2 (0) H \right| \right)^2 = 0 \nonumber \]
\[ \left( \left| V^T W_2 (0) V \right| \right)^2 = 1 \nonumber \]
When a half wave plate is placed between crossed polarizers no light gets through.
\[ \left( \left| V^T W_2 (0) H \right| \right)^2 = 0 \nonumber \]
When the half wave plate is rotated by an angle of \( \pi\)/4 all the light gets through.
\[ \left( \left| V^T W_2 \left( \frac{ \pi}{4} \right) H \right| \right)^2 = 1 \nonumber \]
When the half wave plate is rotated by an additional angle of \( \pi\)/4 no light gets through.
\[ \left( \left| V^T W_2 \left( \frac{ \pi}{2} \right) H \right| \right)^2 = 0 \nonumber \]
When a half wave plate rotated by \( \pi\)/4 is placed between two vertical or horizontal polarizers no light gets through.
\[ \left( \left| V^T W_2 \left( \frac{ \pi}{4} \right) V \right| \right)^2 = 0 \nonumber \]
\[ \left( \left| H^T W_2 \left( \frac{ \pi}{4} \right) H \right| \right)^2 = 0 \nonumber \]
There is no effect when a quarter wave plate is inserted between either aligned or crossed polarizers.
\[ \left( \left| V^T W_4 V \right| \right)^2 = 1 \nonumber \]
\[ \left( \left| H^T W_4 V \right| \right)^2 = 1 \nonumber \]
If the quarter wave plate is rotated by \( \pi\)/4 50% of the light gets through.
\[ \left( \left| V^T BS (V) \right| \right)^2 = 0.5 \nonumber \]
\[ \left( \left| H^T BS (V) \right| \right)^2 = 0.5 \nonumber \]

