6.13: An Extensive Set of Group Theory Problems for Chemists
- Page ID
- 149476
The following table shows the vibrational frequencies of CH4. Assuming CH4 belongs to the Td point group, fill in the gaps in the table. Use S for stretch and B for bend to designate type of vibration.
\[ \begin{pmatrix} \text{Frequency} & 2917 cm^{-1} & 1534 cm^{-1} & 3019 cm^{-1} & 1306 cm^{-1} \\ \text{Stretch or Bend} & \blacksquare & \blacksquare & \blacksquare & \blacksquare \\ \text{Symmetry} & \blacksquare & \blacksquare & \blacksquare & \blacksquare \\ \frac{ \text{Activity}}{ \text{IR or Raman}} & \blacksquare & \blacksquare & \blacksquare & \blacksquare \end{pmatrix} \nonumber \]
The following table shows the vibrational frequencies of CD4. Assuming CD4 belongs to the Td point group, fill in the gaps in the table. Use S for stretch and B for bend to designate type of vibration.
\[ \begin{pmatrix} \text{Frequency} & 2109 cm^{-1} & 1092 cm^{-1} & 2259 cm^{-1} & 966 cm^{-1} \\ \text{Stretch or Bend} & \blacksquare & \blacksquare & \blacksquare & \blacksquare \\ \text{Symmetry} & \blacksquare & \blacksquare & \blacksquare & \blacksquare \\ \frac{ \text{Activity}}{ \text{IR or Raman}} & \blacksquare & \blacksquare & \blacksquare & \blacksquare \end{pmatrix} \nonumber \]
The following table summarizes the infrared activity CH2D2. Assuming it belongs to the C2v point group, complete the table. Use S for stretch and B for bend to designate the type of vibration.
\[ \begin{pmatrix} \text{Frequency} & 2974 & 2202 & 1436 & 1033 & 1333 & 3013 & 1090 & 2234 & 1155 \\ \text{Stretch or Bend} & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare \\ \text{Symmetry} & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare \\ \frac{ \text{Activity}}{ \text{IR or Raman}} & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare \end{pmatrix} \nonumber \]
The following table summarizes the infrared activity of CH3D. Assuming CH3D belongs to the C3v point group, fill in the gaps in the table. Use S for stretch and B for bend to designate type of vibration.
\[ \begin{pmatrix} \text{Frequency} & 2945 cm^{-1} & 2200 cm^{-1} & 1300 cm^{-1} & 3017 cm^{-1} & 1471 cm^{-1} & 1155 cm^{-1} \\ \text{Stretch or Bend} & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare \\ \text{Symmetry} & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare \\ \frac{ \text{Activity}}{ \text{IR or Raman}} & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare \end{pmatrix} \nonumber \]
Formaldehde has vibrational frequencies at 2843, 2776, 1501, 1251, 1746, and 1167 cm-1. How many are IR active and how many are Raman active. Separate them into bends and stretches.
\[ \begin{pmatrix} \text{Frequency} & 2843 & 2776 & 1501 & 1251 & 1746 & 1167 \\ \text{Stretch or Bend} & A_1 & A_1 & A_1 & B_1 & B_2 & B_2 \\ \text{Symmetry} & \text{Stretch} & \text{Stretch} & \text{Bend} & \text{Bend} & \text{Stretch} & \text{Bend} \\ \frac{ \text{Activity}}{ \text{IR or Raman}} & IR,R & IR,R & IR,R & IR,R & IR,R & IR,R \end{pmatrix} \nonumber \]
PH3 (C3v) has IR and Raman active vibrations at 2421, 2327, 1121, and 991 cm-1. PD3 has IR and Raman active vibrations at 1698, 1694, 806 and 730 cm-1. Make assignments in terms of stretches and bends.
The infrared spectrum of BCl3 shows vibrational bands at 995, 480, and 244 cm-1, while Raman bands appear at 995, 471, and 244 cm-1. Is the geometry of the molecule trigonal pyramid (C3v) or trigonal planar (D3h)? Is your answer to this question consistent with chemical bonding principles? Assign symmetry labels to the vibrational bands and identify the stretches and bends.
\[ \begin{pmatrix} \text{Frequency} & 995 cm^{-1} & 480 cm^{-1} & 471 cm^{-1} & 224 cm^{-1} \\ \frac{ \text{Activity}}{ \text{IR or Raman}} & IR,R & IR & R & IR,R \\ \text{Symmetry} & \blacksquare & \blacksquare & \blacksquare & \blacksquare \\ \text{Stretch or Bend} & \blacksquare & \blacksquare & \blacksquare & \blacksquare \end{pmatrix} \nonumber \]
CH3CN has 12 vibrational degrees of freedom, but 8 fundamental vibrational frequencies appear in the infrared at 2999, 2942, 2249, 1440, 1376, 1124, 918, and 380 cm-1. Explain.
The infrared spectrum of methane shows two absorptions: a bend at 1306 cm-1 and a stretch at 3019 cm-1. Demonstrate that a symmetry analysis assuming tetrahedral symmetry for methane is consistent with this spectroscopic data. Also predict how many Raman active modes methane should have.
The infrared spectrum of XeF4 has absorptions at 161, 291, and 586 cm-1 (two bends, one stretch), while the Raman spectrum has peaks at 218, 524, and 554 cm-1 (one bend, two stretches). Is its molecular structure tetrahedral or square planar? References: J. Am. Chem. Soc. 1963, 85, 1927; J. Phys. Chem. 1971, 54, 5247.
Cubane, C8H8, has 42 vibrational degrees of freedom, but only three IR active modes. Cubane belongs to the octahedral point group. Show that group theory predicts three IR active modes. Determine how many vibrational modes will be Raman active. Will there be any coincidences between the IR and Raman active modes? The synthesis and characterization of cubane was reported in 1964 by Philip Eaton and Thomas Cole in JACS 1964, 86, 3157-3158. They reported three IR bands at 3000, 1231, and 851 cm-1.
When Paquette's group synthesized dodecahedrane, C20H20, they measured its infrared and Raman spectra (JACS 1983, 105, 5446-5450). They found three IR active bands at 2945, 1298, and 728 cm-1 and eight Raman frequencies at 2924, 2938, 1324, 1164, 1092, 840, 676, and 480 cm-1. Use group theory to show that these data are consistent with the fact that dodecahedrane has icosahedral symmetry.
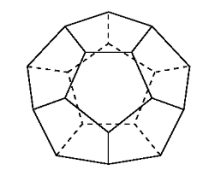
\[ \begin{pmatrix} \text{Frequency cm} & 2938 & 2924 & 1324 & 1164 & 1092 & 840 & 676 & 480 & 2945 & 1298 & 728 \\ \text{Symmetry} & A_g & A_g & H_g & H_g & H_g & H_g & H_g & H_g & T_{1u} & T_{1u} & T_{1u} \\ \frac{ \text{IR, R}}{ \text{Activity}} & R & R & R & R & R & R & R & R & IR & IR & IR \\ \text{Stretch or Bend} & \text{stretch} & \text{stretch} & \text{stretch} & \text{stretch} & \text{stretch} & \text{bend} & \text{bend} & \text{bend} & \text{stretch} & \text{stretch} & \text{bend} \end{pmatrix} \nonumber \]
Sulfur tetrafluoride represents a difficult case which can't be resolved to complete satisfaction on the basis of IR and Raman data alone. The experimental spectra show eight (five certain and three likely) IR bands and eight (five certain and three likely) Raman bands, and eight (five certain and three likely) coincidences between the two. This information plus nmr spectra lead to the conclusion that the symmetry is C2v or the see-saw structure predicted by VSEPR.
The March 28, 2003 issue of Science reported the synthesis and characterization of Al2H6, the aluminum analog of diborane (therefore, dialane). The researchers reported the following experimental IR frequencies in cm-1: B1u (1932, 836); B2u (1268, 632); B3u (1915, 1408,702). Do a symmetry analysis of Al2H6 which belongs to the D2h point group. How many vibrational modes are there? Which ones are IR active and what are their symmetry designations. The researchers reported that one of the expected low frequency vibrations (~200 cm-1) was not observed. What is the symmetry of this vibrational mode?
Buckminsterfullerene (C60) has four IR active vibrational modes (528, 577, 1180, 1430 cm-1) and ten Raman active modes (273, 436, 496, 710, 773, 110, 1250, 1435, 1470, 1570 cm-1). Demonstrate that the assumption of icosahedral symmetry for C60 is consistent with this data.
Do a symmetry analysis of the 60π orbitals of C60 and show that the results are in agreement with a Huckel calculation.
The following Raman and IR frequencies have been observed for the tetrahedral P4 molecule. Is the assignment of tetrahedral geometry to this molecule in agreement with the spectroscopic data? Explain.
\[ \begin{pmatrix} R & R & R,IR \\ \frac{614}{cm} & \frac{372}{cm} & \frac{466}{cm} \end{pmatrix} \nonumber \]
Isotopic subsitution for one of the 31P atoms with a 32P atom reduces the symmetry to C3v. Redo the symmetry analysis and predict the number of IR and Raman active vibrational modes.
Tetrahedrane, C4H4, belongs to the Td point group. Use group theory to predict the number of IR and Raman active vibrational modes it has. Predict also the number of stretches and bends will appear in each type of spectroscopy. To date tetrahedrane has not been synthesized.
Do symmetry analyses on cis-difluoroethene (C2v) and trans-difluoroethene (C2h). Can spectroscopic methods (IR and Raman) be used to distinquish between these isomers. Explain. What about 1,1 difluoroethene? What point group does it belong to? Can spectroscopic methods distinguish it from the cis and trans isomers examined above? Cis-MA2B2 has C2v symmetry and trans-MA2B2 has D2h symmetry. Determine the IR and Raman active modes for each molecule and discuss how such spectroscopic evidence can be used to distinguish the two isomers.
CH3Cl has IR and Raman active modes at 3017, 2937, 1452, 1355, 1017, and 732 cm-1. Is this data consistent with C3v symmetry assignment for chloromethane?
Diborane, D2h, has 18 vibrational degrees of freedom. Nine modes are Raman active and nine are IR active. There are no coincidences. Do a symmetry analysis of diborane to confirm the assignments made in the table below. Identify stretches and bends. The xy plane is the plane of the paper. The four terminal H atoms of diborane lie in the xz plane and the two bridging atoms lie in the xy plane.
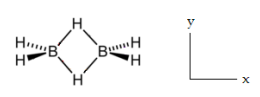
\[ \begin{pmatrix} \text{D}_{2h} & A_g & A_g & A_g & A_g & B_{1g} & B_{1g} & B_{2g} & B_{2g} & B_{3g} \\ \frac{ \text{Raman}}{ \text{cm}} & 2524 & 2104 & 1180 & 794 & 1768 & 1035 & 2591 & 920 & 1012 \\ \text{Stretch or Bend} & S & S & B & B & S & B & S & B & B \\ \text{D}_{2h} & A_u & B_{1u} & B_{1u} & B_{1u} & B_{2u} & B_{2u} & B_{3u} & B_{3u} & B_{3u} \\ \frac{ \text{IR}}{ \text{cm}} & ia & 2612& 950 & 368 & 1915 & 973 & 2525 & 1606 & 1177 \\ \text{Stretch or Bend} & B & S & B & B & S & B & S & S & B \end{pmatrix} \nonumber \]
The following IR and Raman spectroscopic data is available for cyclopropane, C3H6. Demonstrate that this data is consistent with a D3h symmetry assignment for cyclopropane. In addition complete the table below.
\[ \begin{pmatrix} \frac{ \text{Frequency}}{ \text{cm}^{-1}} & 3038 & 1479 & 1188 & 3025 & 1438 & 1029 & 866 & 3103 & 854 & 3082 & 188 & 734 \\ \text{Activity} & IR & IR & IR & R,IR & R,IR & R,IR & R,IR & IR & IR & R & R & R \\ \text{Symmetry} & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare \\ \text{Stretch or Bend} & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare \end{pmatrix} \nonumber \]
\[ \begin{pmatrix} \frac{ \text{Frequency}}{ \text{cm}^{-1}} & 3038 & 1479 & 1188 & 3025 & 1438 & 1029 & 866 & 3103 & 854 & 3082 & 188 & 734 \\ \text{Activity} & IR & IR & IR & R,IR & R,IR & R,IR & R,IR & IR & IR & R & R & R \\ \text{Symmetry} & S & S & B & S & S & B & B & \S & B & S & B & B \\ \text{Stretch or Bend} & A1' & A1' & A1' & E' & E' & E' & E' & A2" & A2" & E" & E" & E" \end{pmatrix} \nonumber \]
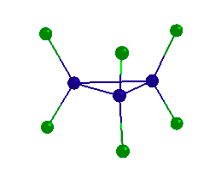
PX5 has trigonal bipyramidal geometry and therefore belongs to the D3h point group. Use the model provided to do a symmetry analysis of PX5 by determining Γuma and Γbonds.
The following spectroscopic information is available.
\[ \begin{pmatrix} \text{Frequency} & 816 cm^{-1} & 648 cm^{-1} & 947 cm^{-1} & 525 cm^{-1} & 1024 cm^{-1} & 533 cm^{-1} & 174 cm^{-1} & 520 cm^{-1} \\ \text{Activity} & R & R & IR & IR & R,IR & R, IR & R, IR & R \\ \text{Symmetry} & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare \\ \text{Stretch or Bend} & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare \end{pmatrix} \nonumber \]
Is the symmetry analysis consistent with the spectroscopic data? Explain in detail.
\[ \begin{pmatrix} \text{Frequency} & 816 cm^{-1} & 648 cm^{-1} & 947 cm^{-1} & 525 cm^{-1} & 1024 cm^{-1} & 533 cm^{-1} & 174 cm^{-1} & 520 cm^{-1} \\ \text{Activity} & R & R & IR & IR & R,IR & R, IR & R, IR & R \\ \text{Symmetry} & A_1 & A_1 & A_2 & A_2 & E & E & E & E \\ \text{Stretch or Bend} & S & S & S & B & S & B & B & B \end{pmatrix} \nonumber \]
The following IR and Raman vibrational data is available for tetrahedral methane. Complete the table. Also show that vibrational data is not consistent with a square planar (D4h) or square pyramid (C4v) geometry.
\[ \begin{pmatrix} \text{Frequency} & 3019 cm^{-1} & 2717 cm^{-1} & 1534 cm^{-1} & 1306 cm^{-1} \\ \text{Activity} & IR,R & R & R & IR, R \\ \text{Symmetry} & \blacksquare & \blacksquare & \blacksquare & \blacksquare \\ \text{Stretch or Bend} & \blacksquare & \blacksquare & \blacksquare & \blacksquare \end{pmatrix} \nonumber \]
The following IR and Raman spectroscopic data is available for ethene, C2H4. Demonstrate that this data is consistent with a D2h symmetry assignment for ethene. In addition complete the table below.
\[ \begin{pmatrix} \text{Frequency} & 3018 & 3106 & 3019 & 2990 & 1623 & 1444 & 1342 & 1236 & 949 & 943 & 810 \\ \text{Activity} & R & IR & R & IR & R & IR & R & R & R & IR & IR \\ \text{Stretch or Bend} & S & S & S & S & S & B & B & B & B & B & B \\ \text{Symmetry} & Ag & B2u & Ag & B3u & B1g & B1u & Ag & B1g & B2g & B2u & B3u \end{pmatrix} \nonumber \]
IR and Raman data forXeOF4, which has C4v symmetry. Establish that the symmetry assignment is correct.
\[ \begin{pmatrix} \text{Frequency cm} & 926 & 576 & 286 & 232 & 220 & 527 & 609 & 364 & 161 \\ \text{Activity} & R,IR & R,IR & R,IR & R & R & R & R,IR & R,IR & R,IR \\ \text{Symmetry} & A_1 & A_1 & A_1 & \frac{B_1}{B_2} & \frac{B_1}{B_2} & B_1 & E & E & E \\ \text{Stretch or Bend} & S & S & B & B & B & S & S & B & B \end{pmatrix} \nonumber \]
IR and Raman data for [PtCl4]2- which has D4h symmetry. Establish that the symmetry assignment is correct.
\[ \begin{pmatrix} \text{Frequency} & 332 cm^{-1} & 320 cm^{-1} & 314 cm^{-1} & 183 cm^{-1} & 170 cm^{-1} & 93 cm^{-1} \\ \text{Activity} & R & IR & R & IR & R & IR \\ \text{Symmetry} & A_{1g} & E_u & B_{1g} & E_u & B_{2g} & A_{2u} \\ \text{Stretch or Bend} & S & S & S & B & B & B \end{pmatrix} \nonumber \]
The vibrational modes of the ions [BrF2]- and [BrF2]+ are given below. Identify which one is A and which one is B.
\[ \begin{bmatrix} A & B \\ 596 (IR) & 715 (IR,R) \\ 442(R) & 706 (IR,R) \\ 198 (IR) & 366(IR,R) \end{bmatrix} \nonumber \]
The following spectroscopic data for [ClO4]- is available. Show that it is consistent with Td symmetry.
\[ \begin{pmatrix} \text{Frequency} & 1102 cm^{-1} & 935 cm^{-1} & 628 cm^{-1} & 462 cm^{-1} \\ \text{Activity} & IR,R & R & IR,R & R \\ \text{Symmetry} & \blacksquare & \blacksquare & \blacksquare & \blacksquare \\ \text{Stretch or Bend} & \blacksquare & \blacksquare & \blacksquare & \blacksquare \end{pmatrix} \nonumber \]
MoF5 has trigonal bipyramidal geometry and therefore belongs to the D3h point group. Use the model provided to do a symmetry analysis of MoF5 by determining Γuma and Γbonds. The following spectroscopic information is available.
\[ \begin{pmatrix} \text{Frequency} & 747 cm^{-1} & 732 cm^{-1} & 703 cm^{-1} & 685 cm^{-1} & 500 cm^{-1} & 440 cm^{-1} & 239 cm^{-1} & 203 cm^{-1} \\ \text{Activity} & R & IR,R & R & IR & IR & R & IR,R & IR,R \\ \text{Symmetry} & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare \\ \text{Stretch or Bend} & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare \end{pmatrix} \nonumber \]
The Raman and IR spectra of a sample of N2F2 are measured and the results are shown below. Is the sample cis-difluordiazine (C2v) or trans-difluordiazine (C2h)?
\[ \begin{pmatrix} \text{Frequency} & 1636 cm^{-1} & 1010 cm^{-1} & 989 cm^{-1} & 592 cm^{-1} & 412 cm^{-1} & 360 cm^{-1} \\ \text{Activity} & R & R & IR & R & IR & IR \\ \text{Symmetry} & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare \\ \text{Stretch or Bend} & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare \end{pmatrix} \nonumber \]
Benzene has IR active modes at 675, 1035, 1479, and 3036 cm-1. Demonstrate that this is consistent with D6h symmetry. Separate the vibrations into stretches and bends.
Do a symmetry analysis of the π orbitals of benzene and show that it is consistent with the results of a Huckel calculation on benzene.
Allene, C3H4, belongs to the D2d point group.
\[ \begin{pmatrix} \frac{ \text{Frequency}}{cm^{-1}} & 3015 & 1443 & 1073 & 865 & 3007 & 1957 & 1398 & 3086 & 999 & 841 & 355 \\ \text{Symmetry} & A_1 & A_1 & A_1 & B_1 & B_2 & B_2 & B_2 & E & E & E & E \\ \text{Bend or Stretch} & S & S & B & B & S & S & B & S & B & B & B \end{pmatrix} \nonumber \]
The following data is available for ethene and deuterated ethene which have D2h symmetry. To each of the vibrational modes determine whether it is a stretch or a bend and its symmetry.
\[ \begin{pmatrix} C_2H_4 & C_2D_4 & \text{Activity} & \frac{ \text{Stretch}}{ \text{Bend}} & \text{Symmetry} \\ 3108 & 2304 & R & \blacksquare & \blacksquare \\ 3106 & 2345 & IR & \blacksquare & \blacksquare \\ 3018 & 2251 & R & \blacksquare & \blacksquare \\ 2990 & 2200 & IR & \blacksquare & \blacksquare \\ 1623 & 1515 & R & \blacksquare & \blacksquare \\ 1444 & 1078 & IR & \blacksquare & \blacksquare \\ 1342 & 981 & R & \blacksquare & \blacksquare \\ 1236 & 1009 & R & \blacksquare & \blacksquare \\ 1007 & 726 & IA & \blacksquare & \blacksquare \\ 949 & 721 & R & \blacksquare & \blacksquare \\ 943 & 780 & IR & \blacksquare & \blacksquare \\ 810 & 586 & IR & \blacksquare & \blacksquare \end{pmatrix} \nonumber \]
BH3 has D3h symmetry. Determine the reducible representation for the hydrogen 1s orbitals (collectively). What linear combination of boron valence orbitals has the same symmetry.
CH4 has Td symmetry. Determine the reducible representation for the hydrogen 1s orbitals (collectively). What linear combination of carbon valence orbitals has the same symmetry.
The following vibrational frequencies are available for cis-dichloroethene. Complete the table assuming that the molecule has C2v symmetry.
\[ \begin{pmatrix} \text{Frequency cm} & 3077 & 1587 & 1179 & 711 & 173 & 876 & 406 & 697 & 3072 & 1303 & 857 & 571 \\ \text{Symmetry} & A_1 & A_1 & A_1 & A_1 & A_1 & A_2 & A_2 & B_1 & B_2 & B_2 & B_2 & B_2 \\ \frac{ \text{IR}}{ \text{Activity}} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{no} & \text{no} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} \\ \frac{ \text{Raman}}{ \text{Activity}} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} \\ \text{Type} & \text{stretch} & \text{stretch} & \text{stretch} & \text{bend} & \text{bend} & \text{bend} & \text{bend} & \text{bend} & \text{bend} & \text{bend} & \text{stretch} & \text{bend} \end{pmatrix} \nonumber \]
The following vibrational frequencies are available for trans-dichloroethene. Complete the table assuming that the molecule has C2h symmetry.
\[ \begin{pmatrix} \text{Frequency cm} & 3073 & 1578 & 1274 & 846 & 350 & 763 & 900 & 227 & 3090 & 1200 & 828 & 250 \\ \text{Symmetry} & A_g & A_g & A_g & A_g & A_g & B_g & A_u & A_u & B_u & B_u & B_u & B_u \\ \frac{ \text{IR}}{ \text{Activity}} & \text{no} & \text{no} & \text{no} & \text{no} & \text{no} & \text{no} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} \\ \frac{ \text{Raman}}{ \text{Activity}} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{no} & \text{no} & \text{no} & \text{no} & \text{no} & \text{no} \\ \text{Type} & \text{stretch} & \text{stretch} & \text{stretch} & \text{bend} & \text{bend} & \text{bend} & \text{bend} & \text{bend} & \text{bend} & \text{bend} & \text{stretch} & \text{bend} \end{pmatrix} \nonumber \]
The following vibrational frequencies are available for 1,1-dichloroethene. Complete the table assuming that the molecule has C2v symmetry.
\[ \begin{pmatrix} \text{Frequency cm} & 3035 & 1627 & 1400 & 603 & 299 & 686 & 875 & 460 & 3130 & 1095 & 800 & 372 \\ \text{Symmetry} & A_1 & A_1 & A_1 & A_1 & A_1 & A_2 & A_2 & B_1 & B_2 & B_2 & B_2 & B_2 \\ \frac{ \text{IR}}{ \text{Activity}} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{no} & \text{no} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} \\ \frac{ \text{Raman}}{ \text{Activity}} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} & \text{yes} \\ \text{Type} & \text{stretch} & \text{stretch} & \text{stretch} & \text{bend} & \text{bend} & \text{bend} & \text{bend} & \text{bend} & \text{bend} & \text{bend} & \text{stretch} & \text{bend} \end{pmatrix} \nonumber \]
Pyrazine has D2h symmetry. Confirm the entries in the following table.
\[ \begin{pmatrix} \text{Symmetry} & A_g & A_g & A_g & A_g & A_g & B_{1g} & B_{2g} & B_{2g} & B_{3g} & B_{3g} & B_{3g} & B_{3g} \\ \text{Frequency cm} & 3054 & 1578 & 1230 & 1015 & 596 & 757 & 919 & 703 & 3041 & 1524 & 1118 & 641 \\ \text{Type} & \text{Stretch} & \text{Stretch} & \text{Stretch} & \text{Bend} & \text{Bend} & \text{Bend} & \text{Bend} & \text{Stretch} & \text{Stretch} & \text{Bend} & \text{Bend} \\ \frac{ \text{Ir, R}}{ \text{Activity}} R & R & R & R & R & R & R & R & R & R & R & R \\ \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ & \circ \\ \text{Symmetry} & A_u & A_u & B_{1u} & B_{1u} & B_{1u} & B_{1u} & B_{2u} & B_{2u} & B_{2u} & B_{2u} & B_{3u} & B_{3u} \\ \text{Frequency cm} & na & 363 & 3066 & 1484 & 1135 & 1021 & 3066 & 1418 & 1346 & 1063 & 804 & 416 \\ \text{Type} & \text{Bend} & \text{Bend} & \text{Stretch} & \text{Stretch} & \text{Bend} & \text{Bend} & \text{Stretch} & \text{Stretch} & \text{Stretch} & \text{Bend} & \text{Bend} & \text{Bend} \\ \frac{ \text{IR,R}}{ \text{Activity}} & IR & IR & IR & IR & IR & IR & IR & IR & IR & IR & IR & IR \end{pmatrix} \nonumber \]
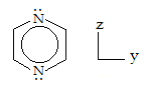
Is the following spectroscopic data consistent with the assignment of D4h symmetry to tetrachloroplatinate, PtCl42-?
\[ \begin{pmatrix} \text{Frequency} & 332 cm^{-1} & 314 cm^{-1} & 170 cm^{-1} & 320 cm^{-1} & 183 cm^{-1} & 93 cm^{-1} \\ \text{Activity} & R & R & R & IR & IR & IR \\ \text{Symmetry} & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare \\ \text{Stretch or Bend} & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare \end{pmatrix} \nonumber \]
\[ \begin{pmatrix} \text{Frequency} & 332 cm^{-1} & 314 cm^{-1} & 170 cm^{-1} & 320 cm^{-1} & 183 cm^{-1} & 93 cm^{-1} \\ \text{Activity} & R & R & R & IR & IR & IR \\ \text{Symmetry} & A_{1g} & B_{1g} & B_{2g} & E_u & A_{2u} & B_{2u} \\ \text{Stretch or Bend} & S & S & B & S & B & B \end{pmatrix} \nonumber \]
Given the following spectroscopic data determine the whether InCl52- has C4v or D3h symmetry.
\[ \begin{pmatrix} \text{Frequency cm} & 294 & 287 & 283 & 274 & 193 & 165 & 143 & 140 & 108 \\ \text{Activity} & IR,R & R & IR,R & IR,R & R & R & IR,R & IR,R & IR,R \\ \text{Symmetry} & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare \\ \text{Stretch or Bend} & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare \end{pmatrix} \nonumber \]
Symmetry analysis supports C4v symmetry as indicated below.
\[ \begin{pmatrix} \text{Activity} & IR & R & \text{Coincidences} \\ \text{Exp} & 6 & 9 & 6 \\ C_{4v} & 6 & 9 & 6 \\ D_{3h} & 5 & 6 & 3 \end{pmatrix} \nonumber \]
Do symmetry analyses on the three C10H8 isomers: azulene (C2v), fulvalene (D2h) and napthalene (D2h). Determine whether IR and Raman spectroscopy can be used to distinguish between the isomers. Completing the table below should facilitate answering the question.
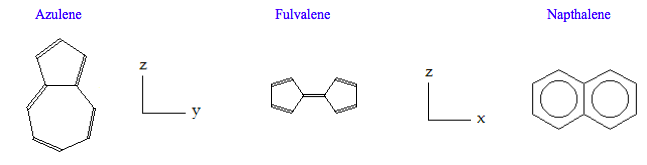
\[ \begin{pmatrix} \text{Molecule} & \frac{ \text{IR}}{ \text{Stretches}} & \frac{ \text{Raman}}{ \text{Stretches}} & \text{Coincidences} & \frac{ \text{IR}}{ \text{bends}} & \frac{ \text{Raman}}{ \text{Bends}} & \text{Coincidences} & \frac{ \text{InActive}}{ \text{ Modes}} \\ \text{Azulene} & 19 & 19 & 19 & 23 & 29 & 23 & 0 \\ \text{Fulvalene} & 9 & 10 & 0 & 11 & 14 & 0 & 4 \\ \text{Napthalene} & 9 & 10 & 0 & 11 & 14 & 0 & 4 \end{pmatrix} \nonumber \]
Propellane has, as shown below, has D3h symmetry. To date it hasn't been synthesized, but theoreticians debate whether or not it has a bridging carbon-carbon bond as shown in the figure. Do a symmetry analysis with and without the bridging bond to determine whether vibrational spectroscopy could decide the issue if the molecule ever became available.
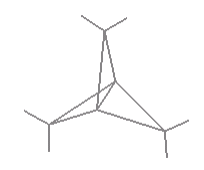
\[ \begin{pmatrix} \text{Propellane} & \frac{ \text{IR}}{ \text{Stretches}} & \frac{ \text{Raman}}{ \text{Stretches}} & \frac{ \text{IR}}{ \text{Bends}} & \frac{ \text{Raman}}{ \text{Bends}} & \frac{ \text{InActive}}{ \text{Modes}} \\ \text{Bond} & 4 & 9 & 4 & 6 & 3 \\ \text{No Bond} & 4 & 8 & 4 & 7 & 3 \end{pmatrix} \nonumber \]
Raman spectroscopy would be required to answer this question, because it indicates one less stretch and one more bend in the vibrational spectroscopy. This makes sense since the number of vibrational degrees of freedom must be conserved. If there is one less bond, there must be one less stretch and therefore one more bend. In this case, the change is observable (hypothetically) in Raman spectroscopy.

