6.7: Ti(H2O)6 3+
- Page ID
- 149285
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This exercise has to do with the interpretation of the visible spectrum Ti(H2O)63+ which is shown below.
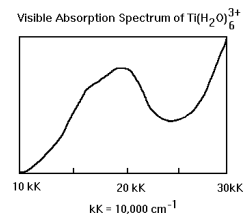
The analysis will begin by assuming that Ti(H2O)63+ has octahedral symmetry. This assumption accounts for the gross features of the spectrum, but does not explain the shoulder that appears on the main absorption peak. The hexaaquatitanium(III) complex is orbitally degenerate and is therefore subject to a Jahn-Teller distortion which reduces the symmetry to square planar. It will be shown that D4h symmetry is fully consistent with the experimental spectrum. The d-orbital energy level diagrams for Oh and D4h symmetry are shown below and will be referred to later in the analysis.

On the basis of these energy level diagrams we would make the following predictions. For octahedral symmetry there is one electronic transition in the visible region. For square planar symmetry there are two electronic transitions in the visible region and one in the infrared. In the analysis that follows it will be shown that none of the electronic transitions is orbitally allowed, but they are allowed through vibronic coupling. Further more the square planar geometry is in better agreement with the experimental spectrum than octahedral symmetry.
Ti(H2O)63+ - Octahedral Symmetry
\[ \begin{matrix} \begin{array} E & & E & C_3 & C_2 & C_4 & C_2" & i & S_{4} & S_{6} & \sigma_h & \sigma_d \end{array} & ~ \\ \text{C}_{Oh} = \begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & -1 & -1 & 1 & 1 & -1 & 1 & 1 & 1 \\ 2 & -1 & 0 & 0 & 2 & 2 & 0 & -1 & 2 & 0 \\ 3 & 0 & -1 & 1 & -1 & 3 & 1 & 0 & -1 & 0 \\ 3 & 0 & 1 & -1 & -1 & 3 & -1 & 0 & -1 & 1 \\ 1 & 1 & 1 & 1 & 1 & -1 & -1 & -1 & -1 \\ 1 & 1 & -1 & -1 & 1 & -1 & 1 & -1 & -1 & 1 \\ 2 & -1 & 0 & 0 & 2 & -2 & 0 & 1 & -2 & 0 \\ 3 & 0 & -1 & 1 & -1 & -3 & -1 & 0 & 1 & 1 \\ 3 & 0 & 1 & -1 & -1 & -3 & 1 & 0 & 1 & -1 \end{bmatrix} & \begin{array} \text{A1g: }x^2 + y^2 + z^2 \\ \text{A2g} \\ \text{Eg: } 2z^2-x^2-y^2,~x^2-y^2 \\ \text{T1g: Rx, Ry, Rz} \\ \text{T2g: }xy,~xz,~yz \\ \text{A1u:} \\ \text{A2u} \\ \text{Eu} \\ \text{T1u: x, y, z} \\ \text{T2u} \end{array} & \text{Oh} = \begin{bmatrix} 1 \\ 8 \\ 6 \\ 6 \\ 3 \\ 1 \\ 6 \\ 8 \\ 3 \\ 6 \end{bmatrix} & \Gamma_{uma} = \begin{bmatrix} 7 \\ 1 \\ 1 \\ 3 \\ 3 \\ 1 \\ 1 \\ 1 \\ 5 \\ 3 \end{bmatrix} \end{matrix} \nonumber \]
\[ \begin{matrix} \text{Ag} = ( \text{C}_{Oh}^T )^{<1>} & \text{A}_{2g} = ( \text{C}_{Oh}^T )^{<2>} & \text{E}_{g} = ( \text{C}_{Oh}^T )^{<3>} & \text{T}_{1g} = ( \text{C}_{Oh}^T )^{<4>} \\ \text{T}_{2g} = (C_{Oh}^T)^{<5>} & \text{A}_{1u} = ( \text{C}_{Oh}^T )^{<6>} & \text{A}_{2u} = ( \text{C}_{Oh}^T )^{<7>} & \text{E}_{u} = ( \text{C}_{Oh}^T )^{<8>} \\ \text{T}_{1u} = ( \text{C}_{Oh}^T )^{<9>} & \text{T}_{2u} = (C_{Oh}^T)^{<10>} & h = \sum \text{Oh} & \Gamma_{tot} = \overrightarrow{( \Gamma_{uma} T1u)}\end{matrix} \nonumber \]
\[ \begin{matrix} \Gamma_{tot}^T = \begin{pmatrix} 21 & 0 & -1 & 3 & -3 & -3 & -1 & 0 & 5 & 3 \end{pmatrix} & \Gamma_{vib} = \Gamma_{tot} - T1u - T1g \end{matrix} \nonumber \]
Determine which irreducible representations contribute to Γvib:
\[ \begin{matrix} i = 1 .. 10 & X_i = \frac{ \sum \overrightarrow{[ Oh (COh^T)^{<i>} \Gamma_{vib}]}}{h} & X^T = \begin{pmatrix} 1 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 2 & 1 \end{pmatrix} \end{matrix} \nonumber \]
Thus we see that: \( \Gamma_{vib} = A1g + Eg + T2g + 2T1u + 2T2u\)
Inspection of the character table shows that in octahedral symmetry the d-orbitals are split into a lower T2g (dxy, dxz, dyz) level and an upper Eg (dz2, dx2-y2) level. Ti3+ has one d-electron in the T2g level. As the spectrum below shows, the complex absorbs in the visible region at 20,000 cm-1 (500 nm). However the T2g ---> Eg transition is orbitally forbidden as is shown below.
\[ \begin{matrix} \int \Psi_{ex} \mu_{e} \Psi_{eg} d \tau_e = 0 & \frac{ \sum \overrightarrow{(Oh~ Eg~ T1u ~T2g)}}{h} = 0 \end{matrix} \nonumber \]
In calculating the transition moment for T2g ---> Eg electronic transition it has been assumed that there was no change in the vibrational state of the molecule. However, it is possible for formally forbidden electronic transitions to become allowed through coupling to changes in vibrational state. In other words pure electronic transitions do not actually occur, because the vibrational (and rotational) states of the molecule change at the same time. These are called vibronic transitions and they are allowed if the integral shown below is nonzero.
\[ \int \int ( \Psi_{ex} \Psi_{vx} \mu_e \Psi_{eg} \Psi_{vg} ) d \tau_e d \tau v \nonumber \]
The calculations below show that vibronic calculations involving the T1u and T2u vibrational modes are allowed because the transition moment is not zero.
\[ \begin{matrix} \frac{ \sum \overrightarrow{(Oh~T1u~Eg~T1u~T2g~A1g)}}{h} = 2 & \frac{ \sum \overrightarrow{(Oh~T1u~Eg~T1u~T2g~A1g)}}{h} = 2\end{matrix} \nonumber \]
At this point we have shown that the vibrationally assisted T2g ---> Eg electronic transition is allowed. However, the shoulder on the experimental spectrum suggest that more than one electronic transition is occuring. In the next section we will see that a reduction to square planar symmetry under the Jahn-Teller effect leads to an d-orbital energy level diagram that is consistent with the experimental spectrum.
Ti(H2O)63+ - Square Planar Symmetry
The Jahn-Teller effect predicts a tetragonal distortion of the octahedral complex to the lower D4h square planar symmetry. The energy level diagram is shown above - essentially the ligands on the z-axis move in toward the titanium ion.
\[ \begin{matrix} ~ & \begin{array} E & C_4 & C_2 & C_2' & C_2" & i & S_4 & \sigma_h & \sigma_v & \sigma_d \end{array} \\ CD4h = & \begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & -1 & -1 & 1 & 1 & 1 & -1 & -1 \\ 1 & -1 & 1 & 1 & -1 & 1 & -1 & 1 & 1 & -1 \\ 1 & -1 & 1 & -1 & 1 & 1 & -1 & 1 & -1 & 1 \\ 2 & 0 & -2 & 0 & 0 & 2 & 0 & -2 & 0 & 0 \\ 1 & 1 & 1 & 1 & 1 & -1 & -1 & -1 & -1 & -1 \\ 1 & 1 & 1 & -1 & -1 & -1 & -1 & -1 & 1 & 1 \\ 1 & -1 & 1 & 1 & -1 & -1 & 1 & -1 & -1 & 1 \\ 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 \\ 2 & 0 & -2 & 0 & 0 & -2 & 0 & 2 & 0 & 0 \end{bmatrix} & \begin{array} A_{1g}:~x^2 + y^2,~z^2 \\ A_{2g}:~Rz \\ B_{1g}:~ x^2-y^2 \\ B_{2g}:~ xy \\ E_{g}:~ \text{(Rx, Ry), (xz, yz)} \\ A_{1u}: \\ A_{2u}:~z \\ B_{1u} \\ B_{2u} \\ E_{u}:~ \text{x, y)} \end{array} & \text{D4h} = \begin{bmatrix} 1 \\ 2 \\ 1 \\ 2 \\ 2 \\ 1 \\ 2 \\ 1 \\ 2 \\ 2 \end{bmatrix} & \Gamma_{uma} = \begin{bmatrix} \\ 1 \\ 1 \\ 3 \\ 1 \\ 1 \\ 1 \\ 5 \\ 3 \\ 1 \end{bmatrix} \end{matrix} \nonumber \]
\[ \begin{matrix} \text{A1g} = ( \text{CD4h}^T )^{<1>} & \text{A2g} = ( \text{CD4h}^T )^{<2>} & \text{B1g} = ( \text{CD4h}^T )^{<3>} & \text{B2g} = ( \text{CD4h}^T )^{<4>} & \text{Eg} = (\text{CD4h}^T)^{<5>} \\ \text{A1u} = ( \text{CD4h}^T )^{<6>} & \text{A2u} = ( \text{CD4h}^T )^{<7>} & \text{B1u} = ( \text{CD4h}^T )^{<8>} \\ \text{B2u} = ( \text{CD4h}^T )^{<9>} & \text{Eu} = ( \text{CD4h}^T)^{<10>} \end{matrix} \nonumber \]
\[ \begin{matrix} h = \sum \text{D4h} & \Gamma_{tot} = \overrightarrow{( \Gamma_{uma} (A2u + Eu))} & \Gamma_{tot}^T = \begin{pmatrix} 15 & 1 & -1 & -3 & -1 & -3 & -1 & 5 & 3 & 1 \end{pmatrix} \end{matrix} \nonumber \]
Symmetry of the vibrational modes.
\[ \begin{matrix} \Gamma_{vib} = \Gamma_{tot} - A2g - Eg - A2u - Eu & i = 1 .. 10 & Y_i = \frac{ \sum \overrightarrow{[D4h (CD4h^T )^{<i>} \Gamma_{vib}]}}{h} \\ Y^T = \begin{pmatrix} 1 & 0 & 1 & 1 & 0 & 0 & 1 & 0 & 1 & 2 \end{pmatrix} & ~ & \Gamma_{vib} = A1g + B1g + B2g + A2u + B2u + 2Eu \end{matrix} \nonumber \]
The energy level diagram above shows three possible electronic transitions, one IR transition and two transitions in visible region of the spectrum. The calculations below show that all three are formally forbidden. Vibronic coupling is invoked to explain the appearance of the two electronic transitions in the visible region.
\[ \begin{matrix} \frac{ \sum \overrightarrow{(D4h~Eg(A2u + Eu)B2g))}}{h} = 0 & \frac{ \sum \overrightarrow{(D4h~B1g(A2u + Eu)B2g))}}{h} = 0 & \frac{ \sum \overrightarrow{(D4h~A1g(A2u + Eu)B2g))}}{h} = 0 \end{matrix} \nonumber \]
A A1u or Eu vibrational mode can provide vibronic coupling for the B2g --> B1g transition.
\[ \begin{matrix} \frac{ \sum \overrightarrow{(D4h~A1u~B1g(A2u + Eu)B2g~A1g))}}{h} = 1 & \frac{ \sum \overrightarrow{(D4h~Eu~B1g(A2u + Eu)B2g~A1g))}}{h} = 1 \end{matrix} \nonumber \]
A B1u or Eu vibrational mode can provide vibronic coupling for the B2g --> A1g transition.
\[ \begin{matrix} \frac{ \sum \overrightarrow{(D4h~B1u~A1g(A2u + Eu)B2g~A1g))}}{h} = 1 & \frac{ \sum \overrightarrow{(D4h~Eu~A1g(A2u + Eu)B2g~A1g))}}{h} = 1 \end{matrix} \nonumber \]
A close examination of the experimental spectrum indicates the presence of two electronic transitions of similar energy (shoulder). So the energy level diagram and the vibronic analysis are consistent with the actual spectrum.

