6.1: Group Theory Principles Applied to H2O
- Page ID
- 149257
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Symmetry Analysis for H2O
Water belongs to the C2v symmetry group and has the following symmetry elements: E, C2z, σxz, and σyz. Its character table is shown below.
\[ \begin{array}{|c|c|c|c|c|c|} \hline \text{C}_{2v} & \text{E} & \text{C}_2^z & \sigma_{xz} & \sigma_{yz} & \text{h = 4} \\ \hline \text{A}_1 & 1 & 1 & 1 & 1 & z,~ x^2,~y^2,~z^2 \\ \hline \text{A}_2 & 1 & 1 & -1 & -1 & \text{xy, R}_z \\ \hline \text{B}_1 & 1 & -1 & 1 & -1 & \text{x, xz, R}_y \\ \hline \text{B}_2 & 1 & -1 & -1 & 1 & \text{y, yz, R}_x \\ \hline \Gamma_{tot} & -9 & -1 & 1 & 3 \\ \hline \end{array} \nonumber \]
The C2v symmetry group has four symmetry elements and four associated symmetry operations. It can be thought of as a four dimensional space with the A1, A2, B1, and B2 irreducible representations playing the role of unite vectors of vector algebra. The irreducible representations span the space and any other vector or representation in that space can be written as a linear combination of them. For simple groups like this character table can be generated by examining how translations along the x-, y-, and z-axes and rotations about these axes transform under the symmetry operations of the group. Using the figure show below you should be able to confirm the designations shown in the right-hand column of the character table. That is the translation in the z-direction transforms like A1, rotation about the z-axis transforms like A2, translation in the x-direction and rotation about the y-axis have symmetry properties represented by B1, and translation in the y-direction and rotation about the x-axis have B2 symmetry. In doing this note (see Atkins) that you record +1 if something is transformed into itself, -1 if it is transformed into minus itself, and 0 if it is transformed into something else under the symmetry operations of the group.
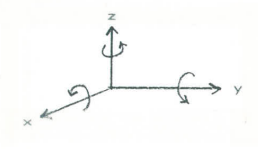
Note that just like the unit vectors in the Cartesian coordinate system, these irreducible representations are orthogonal. That is they have zero overlap.
\[ \begin{matrix} \text{A}_1 \text{B}_2 = \dfrac{[(-1)(1) + (1)(-1) + (1)(-1) + (1)(1)]}{4} = 0 \\ \text{A}_2 \text{B}_1 = \dfrac{[(1)(1) + (1)(-1) + (-1)(1) + (-1)(-1)]}{4} = 0 \end{matrix} \nonumber \]
Dividing by 4, the order of the group, normalizes the calculation. We can also show that all of the irreducible representation are normalized or have an overlap of 1.
\[ \text{A}_2 \text{A}_2 = \dfrac{[(1)(1) + (1)(1) + (-1)(-1) + (-1)(-1)]}{4} = 1 \nonumber \]
Note that these vector operations are exactly equivalent to evaluating quantum mechanical overlap integrals \( \int \Psi_1 \Psi_2 d \tau\).
Since H2O is a triatomic molecule it has a total of 9 degrees of freedom - three for each atom in the molecule. These are the x-, y-, and z-coordinates of the individual atoms and are shown as small vectors located on each of the atoms in the figure below.
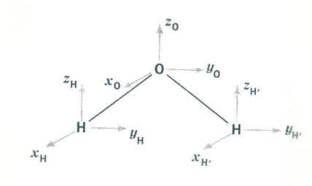
A symmetry analysis for water begins by determining how these 9 coordinates behave under the symmetry operations of the C2v group. You should be able to show that this generates the reducible representation Γtot, which is given in the last row of the character table shown above. Γtot can also be calculated as Γuma (Γx + Γy + Γz), where Γuma is the behavior of the atoms under the symmetry operations of the group. Of the 9 degrees of freedom possessed by the water molecule, three are for translation of the center of mass in the x-, y- and z-directions, and three are related to rotation about the x-, y-, and z-axes. This leaves three vibrational degrees of freedom. To determine the symmetry of the vibrational modes we decompose Γtot into the unit vectors or irreducible representations of the C2v character table. This involves taking the dot product of Γtot with each of the irreducible representations of the C2v symmetry.
\[ \begin{matrix} \Gamma_{tot} \text{A}_1 = \dfrac{[(9)(1) + (-1)(1) + (1)(1) + (3)(1)]}{4} = 3 \\ \Gamma_{tot} \text{A}_2 = \dfrac{[(9)(1) + (-1)(1) + (1)(-1) + (3)(-1)]}{4} = 1 \\ \Gamma_{tot} \text{B}_1 = \dfrac{[(9)(1) + (-1)(-1) + (1)(1) + (3)(-1)]}{4} = 2 \\ \Gamma_{tot} \text{B}_2 = \dfrac{[(9)(1) + (-1)(-1) + (1)(-1) + (3)(1)]}{4} = 3 \end{matrix} \nonumber \]
This procedure has revealed the that the reducible representation, Γtot, is composed of the following irreducible representations:
\[ \Gamma_{tot} = 3 \text{A}_1 + \text{A}_2 + 2 \text{B}_1 + 3 \text{B}_2 \nonumber \]
From the right side of the character table we see that translation and rotation have the following symmetry properties:
\[ \begin{matrix} \Gamma_{trans} = \text{A}_1 + \text{B}_1 + \text{B}_2 \\ \Gamma_{rot} = \text{A}_2 + \text{B}_1 + \text{B}_2 \end{matrix} \nonumber \]
From this information we can determine the symmetry properties of the vibrational modes of the water molecule.
\[ \Gamma_{vib} = \Gamma_{tot} - \Gamma_{trans} - \Gamma_{rot} = 2 \text{A}_1 + \text{B}_2 \nonumber \]
There are three vibrational fundamentals. And, since there are two bonds there will be two stretching vibrations and one bending vibration. To determine which symmetry classification the bend belongs to, examine how the H-O-H bond angle transforms under the symmetry operations of the C2v group.
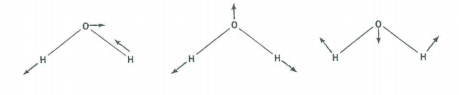
The vibrational modes are shown above. Convince yourself that their symmetry properties are captured in the table below.
\[ \begin{array}{|c|c|c|c|c|c|} \hline \text{C}_{2v} & \text{E} & \text{C}_2^z & \sigma_{xz} & \sigma_{yz} \\ \hline \Gamma_{bend} & 1 & 1 & 1 & 1 & \text{A}_1 \\ \hline \Gamma_{stretch} & 1 & 1 & 1 & 1 & \text{A}_1 \\ \hline \Gamma_{stretch} & 1 & -1 & -1 & 1 & \text{B}_2 \\ \hline \end{array} \nonumber \]
Whether any of these modes is active in the infrared region of the spectrum is another question. This is determined by evaluating the quantum mechanical transition probability integral,
\[ P = e \int \Psi^f (vib) \hat{q} \Psi^i (vib) d \tau \nonumber \]
where q is the spatial coordinate and is either x, y, or z. If this integral is non-zero the transition is allowed. Group theory enables us to determine if the integral is non-zero as follows. We evaluate the direct product (note the similarity to the quantum mechanical transition probability integral) ΓvibfΓqΓvibi and if it turns out to be equal to, or contain, the irreducible representation A1 then the transition is allowed. If the direct product isn't equal to or contain A1 then the transition is forbidden.
Γvibi, the representation for the ground state is always equal to A1 and Γvibf is always equal to A1 and Γvibf has the symmetry of the vibrational mode being excited, which in our case is either A1 or B2. Thus we can see that a vibrational mode will be infrared active if it belongs to the same symmetry species as one of the Cartesian coordinates. You should verify that this is correct and also be able to show that all three vibrational modes of the water molecule are infrared active.
Group theory is also very helpful in constructing molecular orbitals from linear combinations of atomic orbitals. For the water molecule the atomic orbitals are the hydrogen 1s orbitals and the 2s and three 2p orbitals on the oxygen atom. We proceed by examining how the orbitals transform under the symmetry operations of the group. This is shown in the table below.
\[ \begin{array}{|c|c|c|c|c|c|} \hline \text{C}_{2v} & \text{E} & \text{C}_2^z & \sigma_{xz} & \sigma_{yz} \\ \hline \text{H}_1 & \text{H}_1 & \text{H}_2 & \text{H}_2 & \text{H}_1 \\ \hline \text{O}_{2s} & \text{O}_{2s} & \text{O}_{2s} & \text{O}_{2s} & \text{O}_{2s} \\ \hline \text{O}_{2px} & \text{O}_{2px} & - \text{O}_{2px} & \text{O}_{2px} & - \text{O}_{2px} \\ \hline \text{O}_{2py} & \text{O}_{2py} & - \text{O}_{2py} & - \text{O}_{2py} & \text{O}_{2py} \\ \hline \text{O}_{2pz} & \text{O}_{2pz} & \text{O}_{2pz} & \text{O}_{2pz} & \text{O}_{2pz} \\ \hline \text{A}_1 & 1 & 1 & 1 & 1 \\ \hline \text{A}_2 & 1 & 1 & -1 & -1 \\ \hline \text{B}_1 & 1 & -1 & 1 & -1 \\ \hline \text{B}_2 & 1 & -1 & -1 & 1 \\ \hline \end{array} \nonumber \]
To find the molecular orbital with A1 symmetry take the sum of the dot product of the A1 irreducible representation with each of the representations in the top half of the table. This is 2(H1 + H2) + 4O2s + 4O2pz. This indicates that the molecular orbital will consist of a linear combination of four of the six orbitals shown in the table above.
\[ \Psi (A_1) = c_h \left[ \psi (H_1) + \psi (H_2) \right] + c_o \psi (O_{2s}) + c_o \psi (O_{2pz}) \nonumber \]
When this is done for A2 symmetry it is found that the sum is zero, indicating that there is no molecular orbital with A2 symmetry. Repeating this process for B1 symmetry yields 4O2px. This means Ψ(B2) = Ψ(O2px) and we say that the oxygen 2px orbital is non-bonding because there are hydrogen orbitals with the same symmetry. This is easily seen by inspection of the water molecule when placed in a Cartesian coordinate system as shown in the figure above.
For B2 symmetry the result is 2(H1 - H2) + 4O2py. This is clearly another bonding molecular orbital.
\[ \Psi (B_2) = c_h \left[ \psi (H_1) - \psi (H_2) \right] + c_o \psi (O_{2py}) \nonumber \]
The next step is to use the molecular orbitals from this symmetry analysis as the basis for a self-consistent field calculation on the water molecule. This will yield a set of coefficients for the molecular orbitals and a molecular orbital energy level diagram. This results are given below. You should compare these results with the traditional valence bond (Lewis structure) formulation of the bonding in H2O.
\[ \begin{matrix} \Psi (A_1) = 0.15 \left[ \psi (H_1) + \psi (H_2) \right] + 0.82 \psi (O_{2s}) + 0.13 \psi (O_{2pz}) \\ \Psi (B_2) = 0.42 \left[ \psi (H_1) - \psi (H_2) \right] + 0.62 \psi (O_{2py}) \\ \Psi (A_1) = 0.26 \left[ \psi (H_1) + \psi (H_2) \right] - 0.50 \psi (O_{2s}) + 0.79 \psi (O_{2pz}) \\ \Psi (B_1) = \Psi (O_{2px}) \\ \Psi (A_1) = 0.75 \left[ \psi (H_1) + \psi (H_2) \right] - 0.84 \psi (O_{2s}) - 0.70 \psi (O_{2pz}) \\ \Psi (B_2) = 0.89 \left[ \psi (H_1) - \psi (H_2) \right] - 0.99 \psi (O_{2py}) \end{matrix} \nonumber \]
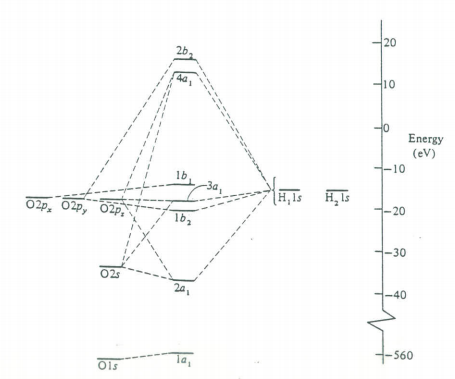
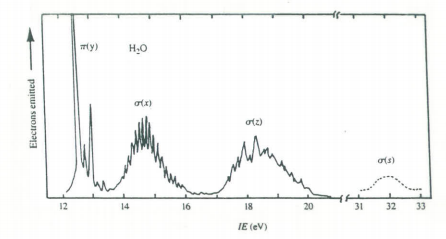
The 1a1 MO is, as would be expected, the oxygen non-valence 1s orbital. The 2a1 MO is mainly a linear combination of the hydrogen 1s and the 2s on oxygen. The 1b2 MO is entirely the oxygen 2py and the hydrogen 1s atomic orbitals. The 3a1 MO and the 1b1 MO correspond to the two long pairs. The 3a1 MO and the 1b1 MO correspond to the two long pairs. The 3a1 MO consists mainly of the oxygen 2s and 2pz and the hydrogen 1s atomic orbitals and has its maximum value in the +z direction. The 1b1 is entirely oxygen 2px and thus is directed at right angles to the plane of the molecule; the lone pairs thus have their maxima in the xz plane.

The first two electronic transitions in water occur at 170 and 130 nm. The molecular orbital diagram obtained previously and the principles of group theory can be used to intepret the electronic spectrum as is shown in the figure below.
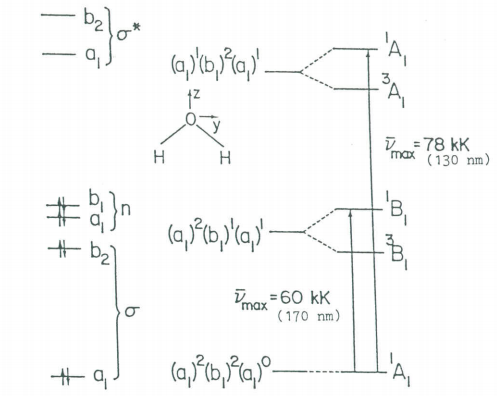
Molecular orbital scheme and state diagram for H2O.
By analogy with IR spectroscopy those electronic transitions are allowed for which the transition moment integral is non-zero.
\[ M = e \int \Psi^f (elec) \hat{q} \Psi^i (elec) d \tau \nonumber \]
As in the case of IR spectroscopy, this integral can be non-zero if and only if ΓvibfΓqΓvibi is equal to or contains the totally symmetric irreducible representation, A1. The figure shows that the electronic ground state has A1 symmetry while the electric dipole operator (μ=eq) has the symmetry of the Cartesian coordinates (A1, B1, B2). Thus ΓvibfΓqΓvibi will equal A1 if the excited state has A1, B1, or B2 symmetry. If this is the case then the transition is said to be orbitally allowed. Note that several orbitally allowed transitions are spin-forbidden (involve a change in spin multiplicity) and therefore do not occur.

