5.24: X-ray Crystallography from a Quantum Mechanical Perspective

According to Richard Feynman1 the double-slit experiment is the paradigm for all of quantum mechanics because it is a simple manifestation of the superposition principle, which is quantum theory’s “only mystery.” In an interesting quantum mechanical analysis of Young’s double-slit experiment, Marcella2 writes the coordinate wave function of the particle interacting with the slit-screen as a linear superposition of being at both slits,

\[ | \Psi \rangle = \frac{1}{ \sqrt{2}} \left[ |x_1 \rangle + | x_2 \rangle \right] \nonumber \]

where x₁ and x₂ are the positions of two infinitesimally thin slits. The diffraction pattern at the detection screen is determined by the momentum distribution at the slit screen. The momentum wave function is obtained by projecting equation (1) into momentum space,

\[ \langle p_x | \Psi \rangle = \frac{1}{ \sqrt{2}} \left[ \langle p_x | x_1 \rangle + \langle p_x | x_2 \rangle \right] = \frac{1}{2 \sqrt{ \pi h}} \left[ exp \left( - \frac{ip_x x_1}{h} \right) + exp \left( - \frac{ip_x x_2}{h} \right) \right] \nonumber \]

where the \( \langle p_x | x_1 \rangle\) are the position eigenfunctions in the momentum representation. The square of the absolute magnitude of this function is shown in Figure 1.

Figure 2.

Figures 1 and 2. In addition, because the particle has been localized at two positions interference effects are prominent in its momentum distribution.

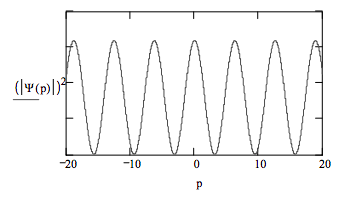
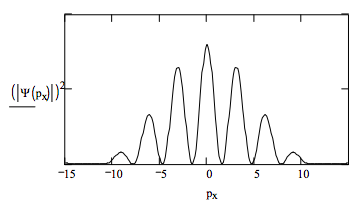
Like the double-slit phenomenon, x-ray diffraction by crystals is also based on the linear superposition principle. For the sake of simplicity attention will be restricted to two-dimensional crystals. Also, following Marcella’s first model, the atoms or ions occupying the lattice sites are considered to be point scatterers. Under these assumptions, the coordinate-space wave function of a photon illuminating a crystal is a superposition of the atomic scattering positions.

\[ | \Psi = \frac{1}{ \sqrt{N}} \sum_{i=1}^N | x_i,~y_i \rangle \nonumber \]

As we wish to know the diffraction pattern that will be found at the detector, we express this superposition in the momentum representation as follows.

\[ \langle p | \Psi \rangle = \frac{1}{ \sqrt{N}} \sum_{i=1}^N \langle p_x | x_i \rangle \langle p_y | y_i \rangle \nonumber \]

Employing the expression for the position wave function in the momentum representation we can convert equation (4) to

\[ \langle p | \Psi \rangle = \frac{1}{ \sqrt{N}(2 \pi h)} \sum_{i=1}^N f_i \text{ exp} \left[ - \frac{i}{h} (p_xx_i + p_yy_i ) \right] \nonumber \]

where the fi are the atomic scattering factors. A face-centered “squaric” arrangement of five atomic point scatterers yields the following diffraction pattern, 2 p Ψ .

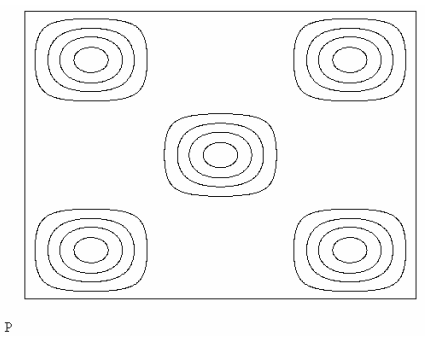
The Mathcad document used to generate this diffraction pattern is shown in the Appendix.

Literature cited:

1. R. P. Feynman, R. B. Leighton, and M. Sands, The Feynman Lectures on Physics, Vol. 3; Addison-Wesley: Reading, 1965.
2. T. V. Marcella, “Quantum interference with slits,” European Journal of Physics 23, 615-621 (2002).

Appendix

\[ \begin{matrix} \text{Number of atoms: } A = 5 & \text{Atomic positions and relative scattering factors:} \end{matrix} \nonumber \]

\[ \begin{matrix} x_1 = 0 & y_1 = 0 & f_1 = \frac{1}{4} & ~ & x_2 = 0 & y_2 = 1 & f_2 = \frac{1}{4} \\ x_3 = 1 & y_3 = 0 & f_3 = \frac{1}{4} & ~ & x_4 = 1 & y_4 = 1 & f_4 = \frac{1}{4} \\ x_5 = \frac{1}{2} & y_5 = \frac{1}{2} & f_5 = \frac{1}{2} \end{matrix} \nonumber \]

\[ \begin{matrix} \Delta = 10 & N = 200 & j = 0 .. N & px_j = - \Delta + \frac{2 \Delta j}{N} & k = 0 .. N & py_k = - \Delta + \frac{2 \Delta k}{N} \end{matrix} \nonumber \]

Fourier transform of position wave function into the momentum representation:

\[ \begin{matrix} \Psi (p_x,~p_y) = \sum_{m=1}^A f_m exp(-i p_x x_m -ip_yy_m ) & P_{j,~k} = \left( \left| \Psi \left( px_j,~py_k \right) \right| \right)^2 \end{matrix} \nonumber \]