5.15: Calculating the Airy Diffraction Pattern

Last updated
Save as PDF

Page ID: 150540

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The Airy diffraction pattern is created by illuminating a screen containing a circular hole with photons. The experiment can be performed with weak sources such that there is only one photon interacting with the screen at a time. This photon-screen interaction constitutes a position measurement.

Screen Shot 2019-05-09 at 12.41.33 PM.png

The position wave function has a constant amplitude within the area of the hole and is shown to be normalized.

\[ \begin{matrix} \Psi (x,~y) = \frac{1}{ \sqrt{ \pi R^2}} & R^2 = x^2 + y^2 & \int_{-R}^{R} \int_{- \sqrt{R^2 - x^2}}^{ \sqrt{R^2 - x^2}} \Psi (x,~y)^2 dy dx = 1 \end{matrix} \nonumber \]

The Airy diffraction pattern is the Fourier transform of the position wave function into the momentum representation. In other words, the interference pattern at the detection screen actually represents a momentum measurement. The following calculations are carried out in atomic units using a hole radius of 0.2.

Hole radius: R = .2

Calculate the Airy diffraction pattern:

\[ \begin{matrix} \Delta = 100 & N = 80 & j = 0 .. N & px_j = - \Delta + \frac{2 \Delta j}{N} & k = 0 .. N & py_k = - \Delta + \frac{2 \Delta k}{N} \end{matrix} \nonumber \]

\[ \begin{matrix} \Phi (p_x,~p_y) = \frac{1}{ \pi} \int_{R}^R \int_{- \sqrt{R^2 - x^2}}^{ \sqrt{R^2 -x^2}} \frac{1}{ \sqrt{ \pi R^2}} exp(-i p_x x) exp(-i p_y y) dy dx & P_{j,~k} = \left( \left| \Phi (px_j,~py_k ) \right| \right)^2 \end{matrix} \nonumber \]

Display the Airy diffraction pattern.

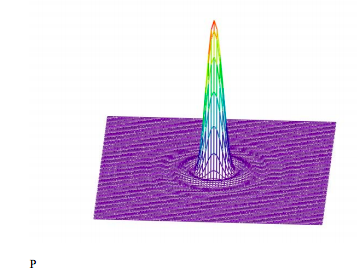
Screen Shot 2019-05-09 at 1.17.09 PM.png

Truncating the high intensity central disk provides a better picture of the outer maxima and minima.

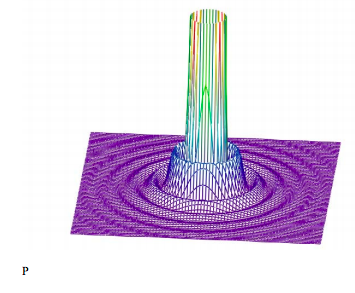
Screen Shot 2019-05-09 at 1.17.17 PM.png

Examining a radial slice of the Airy diffraction pattern provides a simple illustration of the uncertainty principle. Assume that the position uncertainty is given by the diameter of the hole and that the momentum uncertainty is given by the momentum range of the central disk.

\[ \begin{matrix} py = 0 & px = -100,~-99, .. 100 & \Phi (px,~py~R) = \frac{1}{ \pi} \int_{-R}^R \int_{- \sqrt{R^2 - x^2}}^{ \sqrt{R^2 - x^2}} \frac{1}{ \sqrt{ \pi R^2}} exp (-i px x)exp(-i py y) dy dx \end{matrix} \nonumber \]

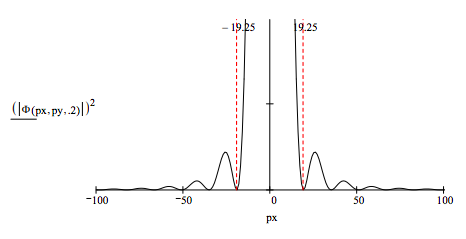
Screen Shot 2019-05-09 at 1.17.23 PM.png

For a diameter of 0.4the position-momentum uncertainty product is: \( 0.4 ~ 38.5 = 15.4\)

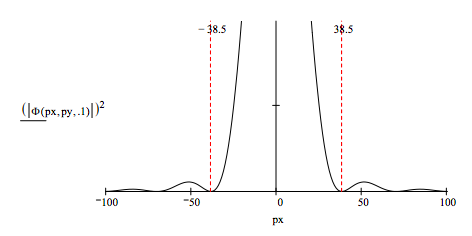
Screen Shot 2019-05-09 at 1.17.28 PM.png

For a diameter of 0.2 the position-momentum uncertainty product is: \(.2 ~77.0 = 15.4\)

The reciprocal relationship between the uncertainty in position and momentum is clearly revealed in this example.