4.4: The Ammonia Inversion and the Maser

Abstract:

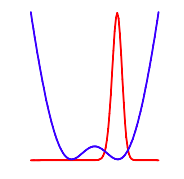
The umbrella inversion in ammonia is modeled as a harmonic potential with an internal Gaussian barrier to inversion. The allowed vibrational eigenstates are calculated by numerical integration of Schrödinger's equation. The significance of the inversion in the operation of the maser is stressed.

Ammonia has four IR active vibrational modes occurring at 3444, 3337, 1627, and 950 cm^-1. The umbrella-like bending mode at 950 cm^-1 is modeled by a harmonic potential well with a Gaussian internal barrier. [See for example: Swallen and Ibers, J. Chem. Phys. 36, 1914 (1962).]

\[ V = \frac{1}{2} kx^2 + b \text{exp} (-c x^2) \nonumber \]

The presence of the Gaussian barrier within the dominant harmonic potential causes a bunching between adjacent symmetric (+) and anti-symmetric (-) states. All states are raised in energy by the presence of the barrier, but the (-) states are elevated less than the (+) states because they have a node in the barrier and the (+) states do not.

Below Schrödinger's equation is integrated numerically for the first four energy states and the results compared with experimental spectroscopic data. (Integration algorithm taken form J. C. Hansen, J. Chem. Educ. Software, 8C2, 1996.)

Set parameters (atomic units are used):

\[ \begin{matrix} n = 99 & xmin = -2 & xmax = 2 & \Delta = \frac{xmax = xmin}{n} \\ \mu = 4668 & k = .07598 & b = .05684& c = 1.36696 \end{matrix} \nonumber \]

Calculate position vector, the potential energy matrix, and the kinetic energy matrix. Then combine them into a total energy matrix.

\[ \begin{matrix} i = 0 .. n & j = 0 .. n & x_i = xmin + (i) \Delta \end{matrix} \nonumber \]

\[ \begin{matrix} V_{i,~j} = \text{if} \left[ i = j,~ \left[ \frac{1}{2} k(x_i)^2 + b \text{exp} \left[ -c (x_i)^2 \right] \right],~0 \right] & T_{i,~j} = \text{if} \left[ i-j,~ \frac{ \pi^2}{6 \mu \Delta^2},~ \frac{(-1)^{i-j}}{(i-j)^2 \mu \Delta^2} \right] \end{matrix} \nonumber \]

Hamiltonian matrix: H = T + V

Find eigenvalues: E = sort(eigenvals(H))

Selected eigenvales: m = 0 .. 3

\[E_m = \begin{array}{|c|} \hline 0.04996046 \\ \hline 0.04996492 \\ \hline 0.05418694 \\ \hline 0.05435966 \\ \hline \end{array} \nonumber \]

Find selected eigenevectors: \( \Psi (m) = \text{eigenvec}(H, ~E_m)\)

Plot selected eigenfunctions: V_poti = V_{i, i}

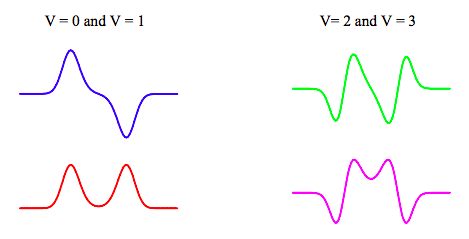
The selection rule for transitions between the manifold of energy levels obtained with this potential is (+ --> -) or (- --> +). A comparison of the first four calculated energy levels with experimental spectroscopic data shows that the Gaussian potential is a good model for the ammonia inversion.

According to the selection rule, there are four allowed transitions between these energy states. Two transitions (E₀ ---> E₁ and E₂ ---> E₃) occur in the microwave region at 0.79 and 36 cm^-1. The E₁ ---> E₀ transition is, of course, the basis for the ammonia maser. The other allowed transitions (E₀ ---> E₃ and E₁ ---> E₂) appear in the infra-red region at 968.3 and 932.5 cm^-1. The E₀ ---> E₂ and E₁ ---> E₃ transitions are forbidden. A comparison between the experimental and calculated frequencies for the allowed transitions is given below.

\[ \begin{matrix} \text{Transition} & \text{Theory/cm}^{-1} & \text{Experiment/cm}^{-1} \\ E_0 \rightarrow E_1 & (E_1 - E_0) 2.1947463 \times 10^5 = 0.98 & 0.79 \\ E_2 \rightarrow E_3 & (E_3 - E_2) 2.1947463 \times 10^5 = 37.9 & 36.0 \\ E_1 \rightarrow E_2 & (E_1 - E_2) 2.1947463 \times 10^5 = 926.6 & 932.5 \\ E_0 \rightarrow E_3 & (E_13- E_0) 2.1947463 \times 10^5 = 965.5 & 968.3 \end{matrix} \nonumber \]

The criteria for allowed transitions are that the photon must satisfy the Bohr frequency condition and that the time-dependent superposition involving the initial and final states must exhibit asymmetric oscillating dipole character. The animation provided in the Appendix allows one to confirm the allowed and forbidden transitions listed above.

The harmonic potential with internal Gaussian function representing the barrier to inversion is shown below:

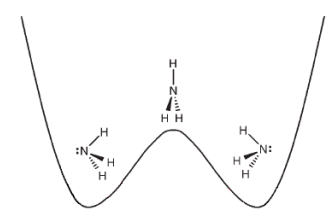
The nitrogen is to the left of the plane of hydrogens in the left-hand well, NH₃, and to the right in the right-hand well H₃N. It is clear from the plots above that the v = 0 and v = 1 wave functions are linear superpositions of these states:

\[ \begin{matrix} | \Psi \rangle_0 = \frac{1}{ \sqrt{2}} \left[ | \ddot{N} H_3 \rangle + |H_3 \ddot{N} \rangle \right] & | \Psi \rangle_1 = \frac{1}{ \sqrt{2}} \left[ | \ddot{N} H_3 \rangle + |H_3 \ddot{N} \rangle \right] \end{matrix} \nonumber \]

These states are equally populated at room temperature because the energy difference separating them is less than 1 cm^-1. However they can be separated electrostatically because they have different dipole moments. The |Ψ>1 state is isolated in a resonant cavity and the v =1 ----> v = 0 transition is induced by 24 GHz micro-waves (see "The Maser", J. P. Gordon, Scientific American, Dec. 1958, page 42).

A few additional comments are in order, because by and large most of the time the ammonia inversion phenomenon is interpreted using classical concepts. In his Scientific American article Gordon juxtaposes the (incorrect) classical explanation with the (correct) quantum mechanical explanation.

For example, regarding molecular vibration Gordon says "The molecule does not vibrate; the broken circles (shown in figures on page 44) merely indicate that the atoms are regarded as simultaneously occupying a number of positions." In other words, each vibrational degree of freedom is represented by a wave function which is a weighted superposition of all possible positions. The molecule is in a stationary state; movement only occurs when the vibrational state is perturbed by electromagnetic radiation.

Regarding the inversion phenomenon Gordon writes the following. "On the classical theory we picture the nitrogen atom flipping back and forth at a characteristic frequency of about 24,000 million vibrations per second, or 24,000 megacycles per second. At any given instant the nitrogen atom is on one side of the hydrogens or on the other. From the quantum point of view the nitrogen has at a given time a certain probability of being on either side - in a sense it is partly on both sides. Moreover, the molecule as a whole has two distinct energy states (see calculations above). The difference in energy between the states equals the energy of a photon with frequency of 24,000 megacycles per second."

In other words, the quantum view states that the so-called inversion frequency is actually the frequency of the photon required to induce a transition between the v = 0 and v = 1 states calculated above.

There is at least one other major misconception regarding the inversion phenomenon -- this is the concept of inversion doubling. Harris and Bertolucci, in their otherwise excellent monograph "Symmetry and Spectroscopy", write "The quantum mechanical consequence of a mutiple-minimum potential well is that there are two states for every one state of the single-minimum state." This certainly seems to imply that you are getting two for the price of one, that the internal barrier is creating new vibrational states.

Actually all that is going on is a bunching of existing states. Sketch the harmonic oscillator eigenfunctions and then compare them with the eigenfunctions for harmonic oscillator with Gaussian internal barrier. The presence of the barrier raises the energy of all states, but raises the energy of the symmetric states more than the antisymmetric states because the antisymmetric states have a node (zero probability) in the barrier and the symmetric states don't have a node.

In summary, the ammonia maser is a stunning illustration of quantum mechanics in action. We should teach the maser phenomenon from the quantum mechanical point of view: classical models are more easily digestable, but unfortunately they are incorrect.

Appendix

The selection rule stated above can be illustrated with an animation of the time-dependent superposition involving the two states involved in a transition. McMillin [J. Chem. Ed. 55, 7 (1978)] has described an appealing model for "quantum jumps" that is referred to as the fluctuating dipole mechanism. The animation shown below is based on McMillin's dipole mechanism. Several other "quantum jump" tutorials on this page are also based on McMillin's mechanism.

The v = 0 to v = 1 transition is allowed because the time-dependent superposition involving these states exhibits oscillating dipole character. The ammonia molecule oscillates asymmetrically in time within the left and right potential wells providing a mechanism for coupling with the oscillating electromagnetic field as long as the Bohr frequency condition is satisfied.

The v = 0 to v = 2 transition is forbidden because the time-dependent superposition involving these states does not exhibit oscillating dipole character. The ammonia molecule oscillates symmetrically in time within the left and right potential well and does not provide a mechanism for coupling with the external electromagnetic field.

Select quantum numbers of initial and final states:

\[ \begin{matrix} vi = 0 & vf = 1 \end{matrix} \nonumber \]

\[ \begin{matrix} \text{Energy of transition:} & \Delta E = E_{vf} - E_{vi} & \Delta E = 4.45734266 \times 10^{-6} & t = \frac{ \text{FRAME}}{ 10^{-8}} \end{matrix} \nonumber \]

Time-dependent superposition of initial and final states:

\[ \Phi_i = \frac{ \Psi(vi)_i exp(-i E_{vi}t) + \Psi (vf)_i exp(-i E_{vf}t)}{ \sqrt{2}} \nonumber \]

To animate click on Tools, Animation, Record and follow the instructions in the dialog box. Recommended setting: From 0 To 40 in 10 Frames/Sec.