2.20: Exploring the Role of Lepton Mass in the Hydrogen Atom

Under normal circumstances the the hydrogen atom consists of a proton and an electron. However, electrons are leptons and there are two other leptons which could temporarily replace the electron in the hydrogen atom. The other leptons are the muon and tauon, and their fundamental properties, along with those of the electron, are given in the following table.

\[ \begin{pmatrix} \text{Property} & e & \mu & \tau \\ \frac{ \text{Mass}}{m_e} & 1 & 206.8 & 3491 \\ \frac{ \text{Effective Mass}}{m_e} & 1 & 185.86 & 1203 \\ \frac{ \text{Life Time}}{s} & \text{Stable} & 2.2(10)^{-6} & 3.0(10)^{-13} \end{pmatrix} \nonumber \]

The purpose of this exercise is to demonstrate the importance of mass in atomic systems, and therefore also kinetic energy. Substitution of the deBroglie relation (λ = h/mv) into the classical expression for kinetic energy yields a quantum mechanical expression for kinetic energy. It is of utmost importance that in quantum mechanics, kinetic energy is inversely proportional to mass.

\[ T = \frac{1}{2} mv^2 = \frac{h^2}{2m \lambda} \nonumber \]

A more general and versatile quantum mechanical expression for kinetic energy is the differential operator shown below, where again mass appears in the denominator. An Approach to Quantum Mechanics outlines the origin of kinetic energy operator.

Atomic units (e = m_e = h/2π = 4πε_o = 1) will be used in the calculations that follow. Please note that μ in the equations below is the effective mass and not a symbol for the muon.

Kinetic energy operator:

\[ T = - \frac{1}{2 \mu r} \frac{d^2}{dr^2} ( r \blacksquare ) \nonumber \]

Potential energy operator:

\[ V = - \frac{1}{r} \blacksquare \nonumber \]

Variational trial wave function with variational parameter β:

\[ \Psi (r,~ \beta ) = \left( \frac{ \beta^3}{ \pi} \right)^{ \frac{1}{2}} \text{exp}( - \beta r) \nonumber \]

Evaluation of the variational energy integral:

\[ \begin{array}{c|c} E ( \beta,~ \mu ) = \int_0^{ \infty} \Psi (r,~ \beta ) \left[ - \frac{1}{2 \mu r} \frac{d^2}{dr^2} (r \Psi (r,~ \beta )) \right] 4 \pi r^2 dr ... & _{ \text{simplify}}^{ \text{assume, } \beta > 0} \rightarrow \frac{ \beta^2}{2 \mu} - \beta \\ + \int_0^{ \infty} \Psi (r,~ \beta ) - \frac{1}{r} \Psi (r,~ \beta ) 4 \pi r^2 dr \end{array} \nonumber \]

Minimize the energy with respect to the variational parameter β.

\[ \frac{d}{d \beta} E( \beta,~ \mu+ 0 \text{ solve, } \beta \rightarrow \mu \nonumber \]

Express energy in terms of reduced mass:

\[ E( \beta, ~ \mu ) \text{ substitute, } \beta = \mu \rightarrow - \frac{ \mu}{2} \nonumber \]

Using the virial theorem, the kinetic and potential energy contributions are:

\[ \begin{matrix} T = \frac{ \mu}{2} & V = - \mu \end{matrix} \nonumber \]

Express the trial wave function in terms of reduced mass.

\[ \Psi (r,~ \beta ) \text{ substitute, } \beta = \mu \rightarrow \frac{e^{- \mu r} \sqrt{ \mu^3}}{ \sqrt{ \pi}} \nonumber \]

Demonstrate the effect of mass on the radial distribution function with plots of mass equal to 0.5, 1 and 2.

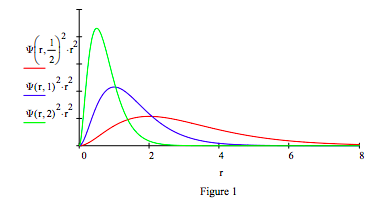
Calculate the expectation value for position to show that it is consistent with the graphical representation above. The more massive the lepton the closer it is on average to the proton.

\[ \int_0^{ \infty} \Psi (r,~ \mu) r \Psi (r,~ \mu) 4 \pi r^2 \text{dr assume, } \mu >0 \rightarrow \frac{3}{2 \mu} \nonumber \]

Summarize the calculated values for the physical properties of H_e, H_μ and H_τ.

\[ \begin{pmatrix} \text{Species} & \frac{E}{E_h} & \frac{T}{E_h} & \frac{V}{E_h} & \frac{r_{avg}}{a_o} \\ H_e & \frac{-1}{2} & \frac{1}{2} & -1 & \frac{3}{2} \\ H_{ \mu} & -92.93 & 92.93 & -185.86 & 8.07(10)^{-3} \\ H_{ \tau} & -601.5 & 601.5 & -1203 & 1.25 (10)^{-3} \end{pmatrix} \nonumber \]

Now imagine that you have a regular hydrogen atom in its ground state and the electron is suddenly by some mechanism replaced by a muon. Nothing has changed from an electrostatic perspective, but the change in energy and average distance of the lepton from the proton are very large. The ground state energy and the average distance from the nucleus decrease by a factor of 185.6, the ratio of the effective masses of the electron and the muon.

This mass effect provides a challenge for those who think all atomic physical phenomena can be explained in terms of electrostatic potential energy effects. Of course, there is an even bigger problem for the potential energy aficionados, and that is the fundamental issue of atomic and molecular stability. Quantum mechanical kinetic energy effects are required to explain the stability of matter.

A Fourier transform of the coordinate wave function yields the corresponding momentum distribution and the opportunity to create a visualization of the uncertainty principle.

\[ \begin{array}{c|c} \Phi (p,~ \mu ) = \frac{1}{4 \sqrt{ \pi^3}} \int_0^{ \infty} \text{exp(-i p r)} \Psi (r,~ \mu) 4 \pi r^2 dr & _{ \text{simplify}}^{ \text{assume, } \mu > 0} \rightarrow \frac{2 \mu^{ \frac{3}{2}}}{ \pi ( \mu + p ~ i)^3} \end{array} \nonumber \]

Figure 2 shows that the most massive particle has the most delocalized momentum distribution. This is consistent with the uncertainty principle which states less spatial uncertainty is accompanied by greater uncertainty in the momentum distribution.

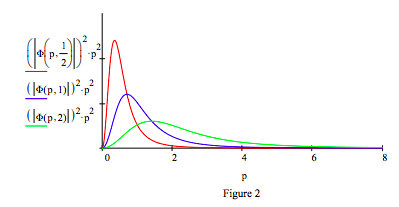
Replacing the proton with a positron, the electron's anti-particle, creates another exotic atom, positronium (Ps). In its singlet ground state electron-positron annihilation occurs in 125 ps creating two γ rays. Positronium's (μ = 1/2) spatial and momentum distributions are shown in Figures 1 and 2. A revised table including positronium is provided below.

\[ \begin{pmatrix} \text{Species} & \frac{E}{E_h} & \frac{T}{E_h} & \frac{V}{E_h} & \frac{r_{avg}}{a_o} \\ H_e & \frac{-1}{2} & \frac{1}{2} & -1 & \frac{3}{2} \\ H_{ \mu} & -92.93 & 92.93 & -185.86 & 8.07(10)^{-3} \\ H_{ \tau} & -601.5 & 601.5 & -1203 & 1.25 (10)^{-3} \\ Ps & - \frac{1}{4} & \frac{1}{4} & - \frac{1}{2} & 3 \end{pmatrix} \nonumber \]