1.76: A Graphical Illustration of the Heisenberg Uncertainty Relationship
- Page ID
- 156477
According to quantum mechanics position and momentum are conjugate variables; they cannot be simultaneously known with high precision. The uncertainty principle requires that if the position of an object is precisely known, its momentum is uncertain, and vice versa. This reciprocal relationship is captured by the well-known uncertainty relation, which says that the product of the uncertainties in position and momentum must be greater than or equal to Planck's constant divided by 4\(\pi\).
\[
\Delta x \cdot \Delta p \geq \frac{h}{4 \cdot \pi}
\nonumber \]
This simple mathematical relation can be visualized using the traditional work horse - the quantum mechanical particle in a box (infinite one-dimensional potential well). The particle's ground-state wave function in coordinate space for a box of width a is shown below.
\[
\Psi(x, a) :=\sqrt{\frac{2}{a}} \cdot \sin \left(\frac{\pi \cdot x}{a}\right)
\nonumber \]
To illustrate the uncertainty principle and the reciprocal relationship between position and momentum, \(\Psi\)(x,a) is Fourier transformed into momentum space yielding the particle's ground-state wave function in the momentum representation.
\[
\Phi(p, a) :=\sqrt{\frac{1}{2 \cdot \pi}} \cdot \int_{0}^{a} \exp (-i \cdot p \cdot x) \cdot \sqrt{\frac{2}{a}} \cdot \sin \left(\frac{\pi \cdot x}{a}\right) d x \; \text{simplify}\rightarrow \frac{\pi \cdot a \cdot\left(e^{-a \cdot p \cdot i}+1\right) \cdot \sqrt{\frac{1}{a}}}{\pi^{\frac{5}{2}}-\sqrt{\pi} \cdot a^{2} \cdot p^{2}}
\nonumber \]
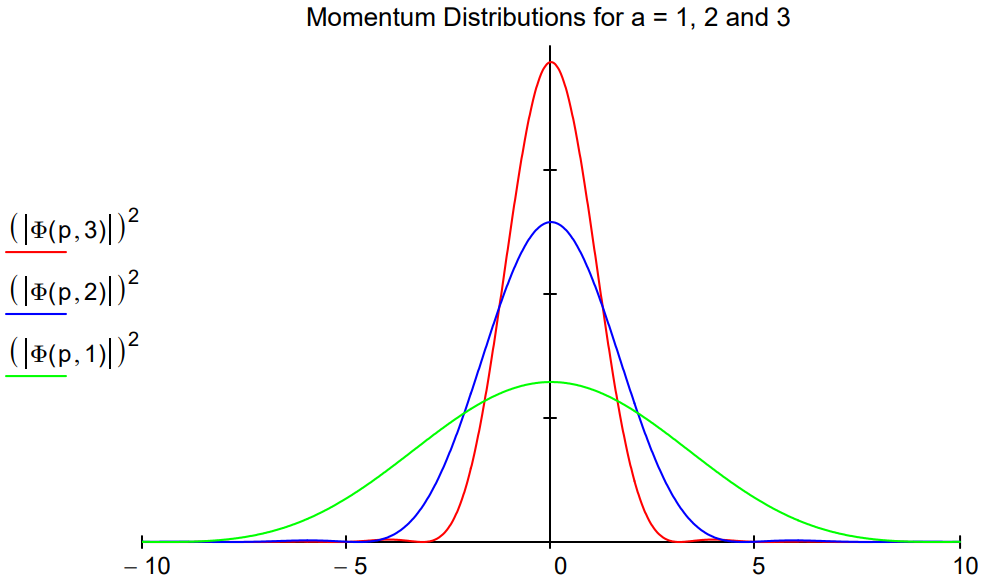
In the figure below, the momentum distribution, |\(\Phi\)(p,a)|2, is shown for three sizes, a = 1,2 and 3. The uncertainty principle is illustrated as follows: as the box size increases the position uncertainty increases and momentum uncertainty decreases because the momentum distribution narrows.