1.8: Quantum Computation- A Short Course
- Page ID
- 136998
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)If you are asked if two pieces of glass have the same thickness, the conventional thing to do is to measure the thickness of each piece – two measurements. As shown in the first two tutorials a double-slit apparatus and a Mach-Zehnder interferometer can answer the question with a single measurement. The third tutorial is a version of the first which shows how path information destroys interference and how the interference can be restored. The fourth tutorial summarizes David Deutsch’s solution to an equivalent mathematical problem using a function introduced earlier. The double-slit apparatus, the Mach-Zehnder interferometer and Deutsch’s circuit are quantum computers which use superpositions and interference effects to cut the effort of answering the question by a factor of two.
Simulating the Deutsch‐Jozsa Algorithm with a Double‐Slit Apparatus
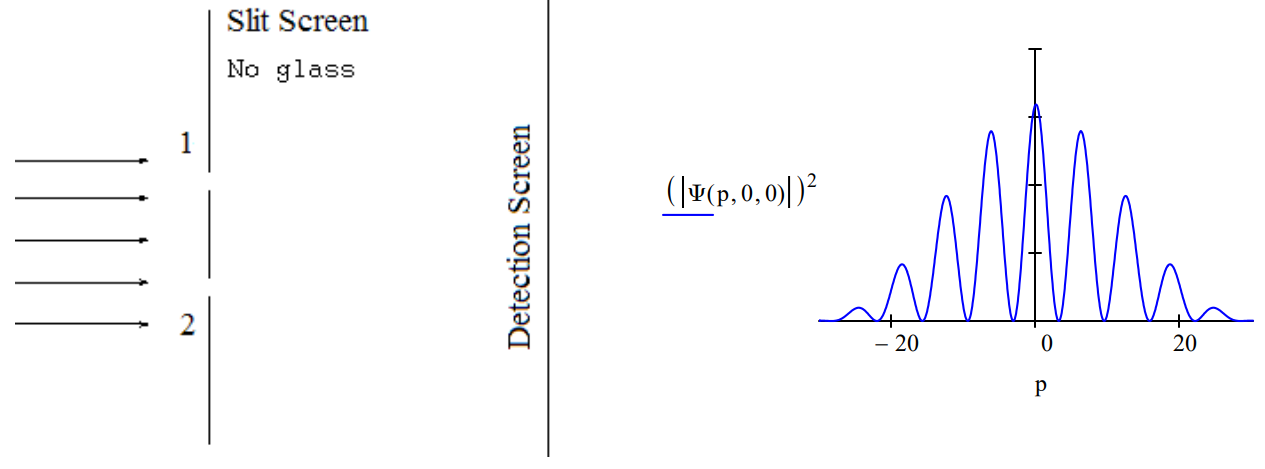
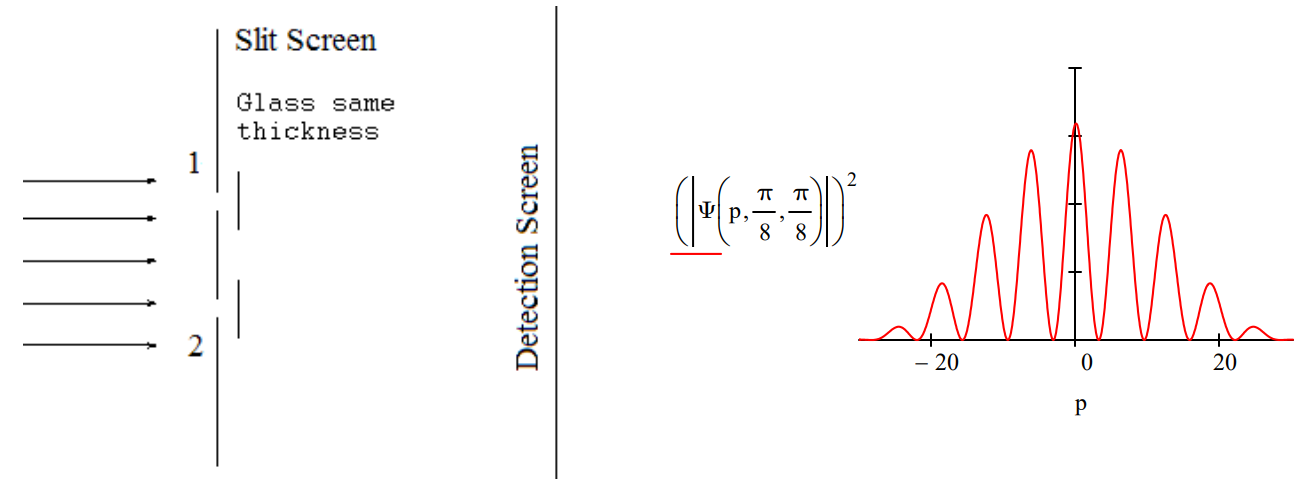
The Deutsch‐Jozsa algorithm determines if either [1] 2N numbers are either all 0 or all 1 (a constant function), or [2] half are 0 and half are 1 (a balanced function) in one step instead of up to 2N‐1 + 1 steps. For N = 1, the Deutsch‐Jozsa algorithm can be visualized as putting two pieces of glass, which may be thin (0) or thick (1), behind the apertures of a double‐slit apparatus and measuring the interference pattern of a light source illuminating the slits. If the pattern is unchanged compared to the empty apparatus, the glass pieces have the same thickness (constant function); otherwise they have different thickness (balanced function). Peter Pfeifer, ʺQuantum Computation,ʺ Access Science, Vol. 17, p. 678, slightly modified by F.R.
This is demonstrated by calculating the diffraction pattern without glass present, and with glass present of the same thickness and different thickness. The diffraction pattern is the momentum distribution, which is the Fourier transform of the slit geometry.
Slit positions:
\[ \mathrm{x}_{\mathrm{L}} =1 \quad \mathrm{x}_{\mathrm{R}} =2 \nonumber \]
Slit width:
\[ \delta : =0.2 \nonumber \]
The momentum wave function with possible phase shifts \(\theta\) and \(\phi\) at the two slits is represented by the following superposition. The phase shifts are directly proportional to the thickness of the glass.
\[
\Psi(\mathrm{p}, \theta, \varphi) = \dfrac{\int_{x_{L}-\frac{\delta}{2}}^{x_{L}+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-i \cdot p \cdot x) \cdot \frac{1}{\sqrt{\delta}} d x \cdot \exp (i \cdot \theta)+\int_{x_{R} \frac{\delta}{2}}^{x_{R}+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-i \cdot p \cdot x) \cdot \frac{1}{\sqrt{\delta}} d x \cdot \exp (i-\varphi)}{\sqrt{2}}
\nonumber \]
The diffraction patterns (momentum distributions) for the empty apparatus (\(\theta = \phi = 0\)), for an apparatus with glass pieces of the same thickness (\(\theta = \phi = \frac{\pi}{8}\)) and for one that has glass of different thickness (\(\theta = \frac{\pi}{8}\; \phi = \frac{\pi}{2}\)) behind the slits are displayed below.
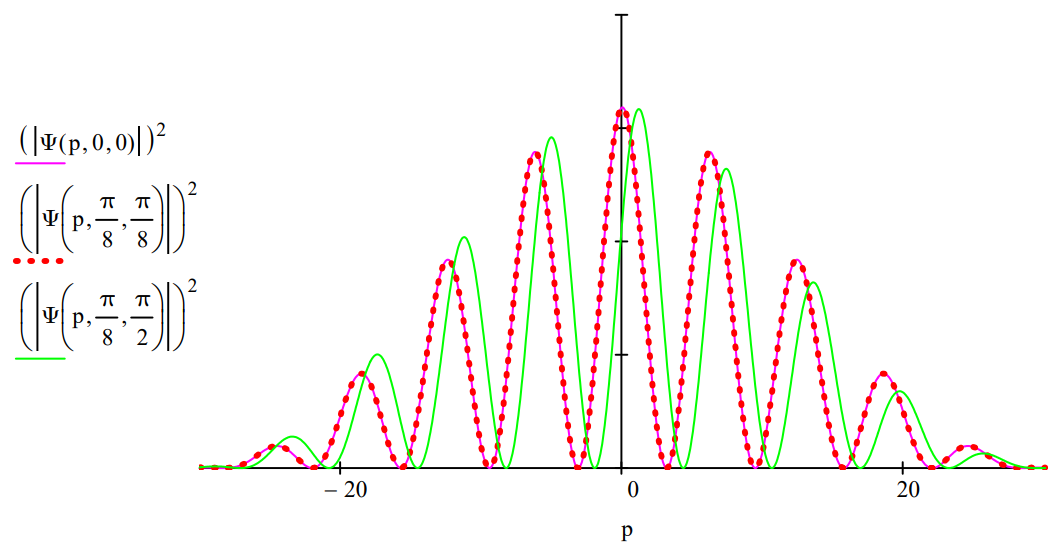
Another look at the calculations with graphical support on the left is provided below.
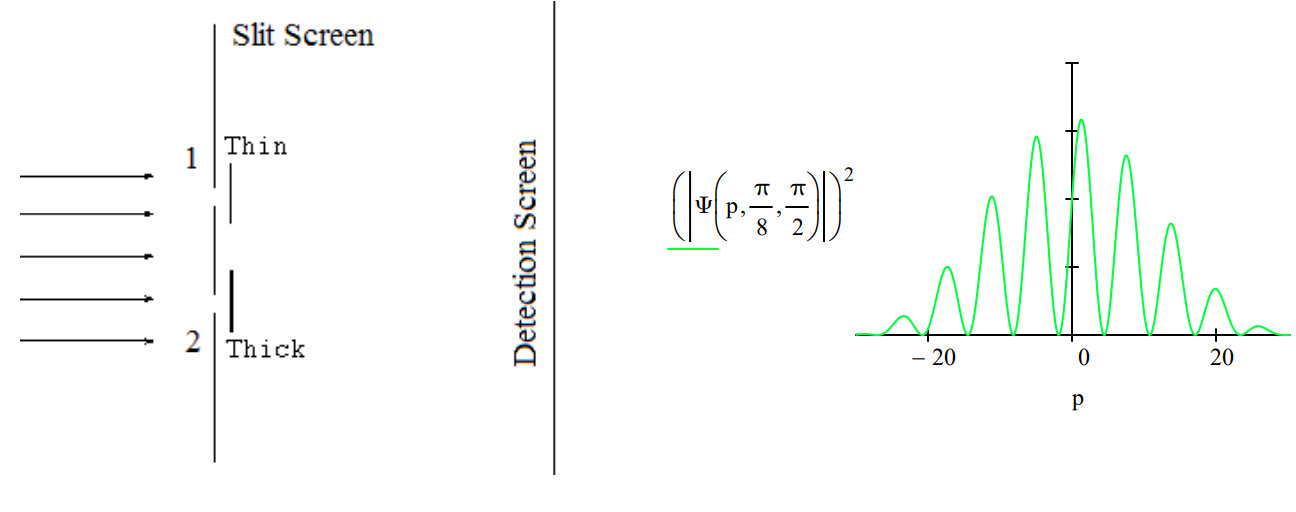
Simulating a Quantum Computer with a Mach-Zehnder Interferometer
Suppose you are asked if two pieces of glass are the same thickness. The convential thing to do is to measure the thickness of each piece of glass and then compare the results. As David Deutsch pointed out this is overkill. You were asked only if they were the same thickness, but you made two measurements to answer that question, when in fact it can be done with one.
Quantum mechanics provides two ways to answer the question; using a double-slit apparatus or a Mach-Zehnder interferometer. They both operate on the same quantum principles. Using the double-slit apparatus you put a piece of glass behind each of the slits and shine light on the slits. If the resulting diffraction pattern is symmetrical about the center of the slits, the glasses are the same thickness. See the previous tutorial: Simulating the Deutsch-Jozsa Algorithm with a Double-Slit Apparatus.
Alternatively you could put a piece of glass in each arm of an equal-arm Mach-Zehnder interferometer (MZI). How this approach works is the subject of this tutorial. First we need to get acquainted with a MZI.
As shown in the following figure a MZI consists of a photon source, two 50-50 beam splitters, two mirrors and two detectors. The Appendix contains the mathematical information necessary to carry out a matrix mechanics analysis of the operation of the interferometer. The motional states of the photon are represented by vectors, while the beam splitters and mirrors are represented by matrices and operate on the vectors.
Yogi Berra has famously said "When you come to a fork in the road, take it." This is exactly what the photon does at a beam splitter. After the first beam splitter the photon, which was moving in the x-direction being emitted by the source, is now in a superposition of moving in both the x- and y-directions. It has been transmitted and reflected at the beam splitter. By convention a 90 degree (\(\frac{\pi}{2}, i\)) phase shift is assigned to reflection.
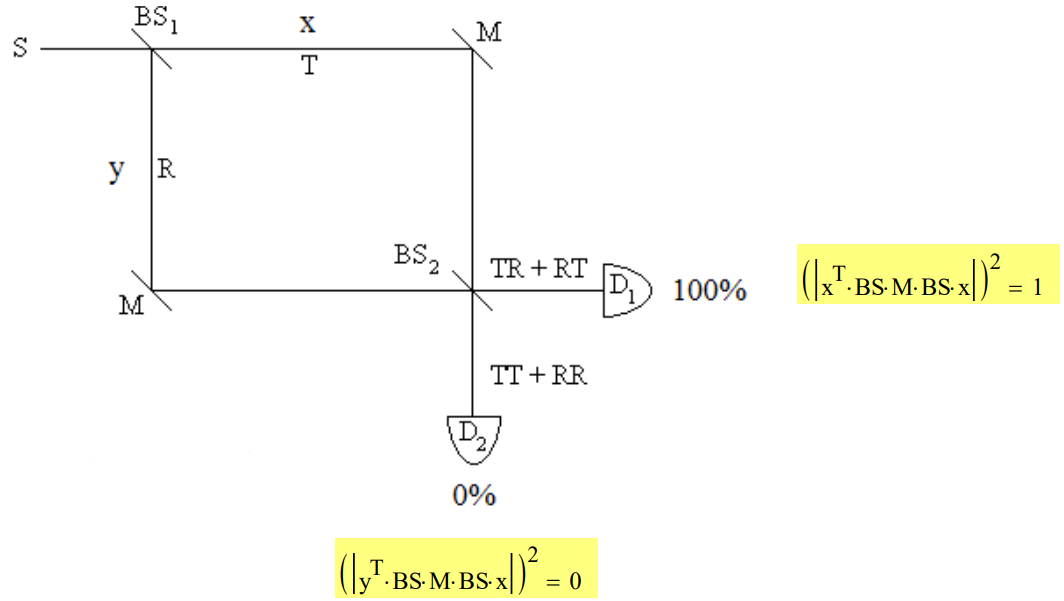
The following calculations illustrate the formation of the superposition state created by the photon's interaction with the first beam splitter.
\[
\mathrm{BS} \cdot \mathrm{x} \rightarrow \left( \begin{array}{c}{\frac{\sqrt{2}}{2}} \\ {\frac{\sqrt{2} \cdot \mathrm{i}}{2}}\end{array}\right) \qquad \mathrm{S}=\frac{1}{\sqrt{2}} \cdot(\mathrm{T}+\mathrm{iR}) \quad \frac{1}{\sqrt{2}} \cdot x+\frac{i}{\sqrt{2}} \cdot y \rightarrow \left( \begin{array}{c}{\frac{\sqrt{2}}{2}} \\ {\frac{\sqrt{2} \cdot i}{2}}\end{array}\right)
\nonumber \]
After the initial beam splitter, the mirrors direct the transmitted and reflected photon states to a second beam splitter where they are recombined. The consequence of this in an equal arm MZI is that the photon is alway registered at D1. There are two paths (histories) to each detector and the amplitudes for these paths interfere. To reach D1 both paths experience one reflection and so arrive in phase with each other with their phases shifted by 90 degrees. The paths to D2, however, are 180 degrees out of phase and destructively interfere. The photon is never detected at D2.
A photon entering the MZI in the x-direction exits in the x-direction phase-shifted by 90 degrees:
\[
\mathrm{BS} \cdot \mathrm{M} \cdot \mathrm{BS} \cdot \mathrm{x} \rightarrow \left( \begin{array}{c}{\mathrm{i}} \\ {0}\end{array}\right) \qquad \mathrm{i} \cdot \mathrm{x} \rightarrow \left( \begin{array}{l}{\mathrm{i}} \\ {0}\end{array}\right)
\nonumber \]
The highlighted areas above next to the detectors show the matrix mechanics calculations for the probability of the photon being registered at D1 and D2. The equations are read from the right. A photon moving in the x-direction interacts with a beam splitter, a mirror and another beam splitter. This state is then projected onto x- and y-direction motion to calculate which detector will register the photon. The absolute square of this calculation (the probability amplitude) is the probability.
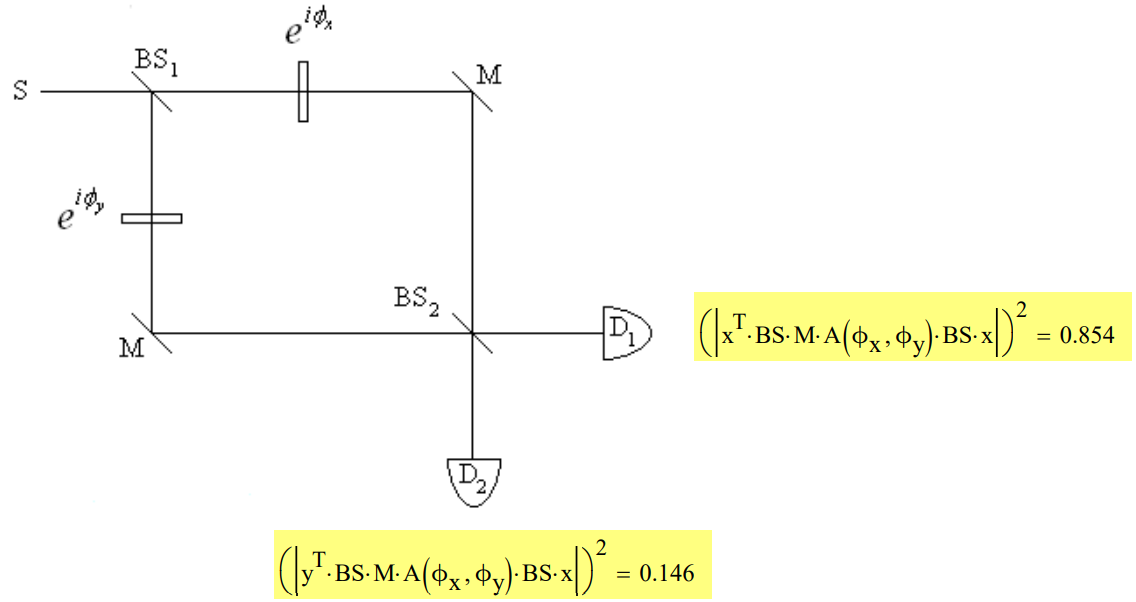
Now we place the pieces of glass in the arms of the interferometer as shown below. The speed of light in glass is different from that in air. Therefore glass causes a phase shift depending on its thickness as is shown below. If the pieces of glass are the same thickness, \(\delta\), they will cause the same phase shift and the photon will be detected at D1. However, if they have different thicknesses, the phase shifts will be different in the two arms of the interferometer. For example, if \(\phi x\) is \(\frac{\pi}{2}\) and \(\phi y\) is \(\frac{\pi}{4}\) then D2 will fire almost 15% of the time indicating that the glasses are not the same thickness.
\[
\phi_{\mathrm{x}}=2 \cdot \pi \cdot \frac{\delta_{\mathrm{x}}}{\lambda} \qquad \phi_{\mathrm{x}} =\frac{\pi}{2} \qquad \phi_{\mathrm{y}}=2 \cdot \pi \cdot \frac{\delta_{\mathrm{y}}}{\lambda} \qquad \phi_{\mathrm{y}} =\frac{\pi}{4}
\nonumber \]
- Appendix:
-
State Vectors
Photon moving horizontally:
\[
\mathbf{x} \equiv \left( \begin{array}{l}{1} \\ {0}\end{array}\right)
\nonumber \]Photon moving vertically:
\[
\mathrm{y} \equiv \left( \begin{array}{l}{0} \\ {1}\end{array}\right)
\nonumber \]Operators
Operator representing a beam splitter:
\[
\mathrm{BS} \equiv \frac{1}{\sqrt{2}} \cdot \left( \begin{array}{cc}{1} & {\mathrm{i}} \\ {\mathrm{i}} & {1}\end{array}\right)
\nonumber \]Operator representing interaction with glass:
\[
A\left(\phi_{x}, \phi_{y}\right) \equiv \begin{pmatrix} e^{i \cdot \phi_{x}} & 0 \\ 0 & e^{i \cdot \phi_{y}} \end{pmatrix}
\nonumber \]Operator representing a mirror:
\[
M \equiv \left( \begin{array}{ll}{0} & {1} \\ {1} & {0}\end{array}\right)
\nonumber \]
Which Path Information and the Quantum Eraser
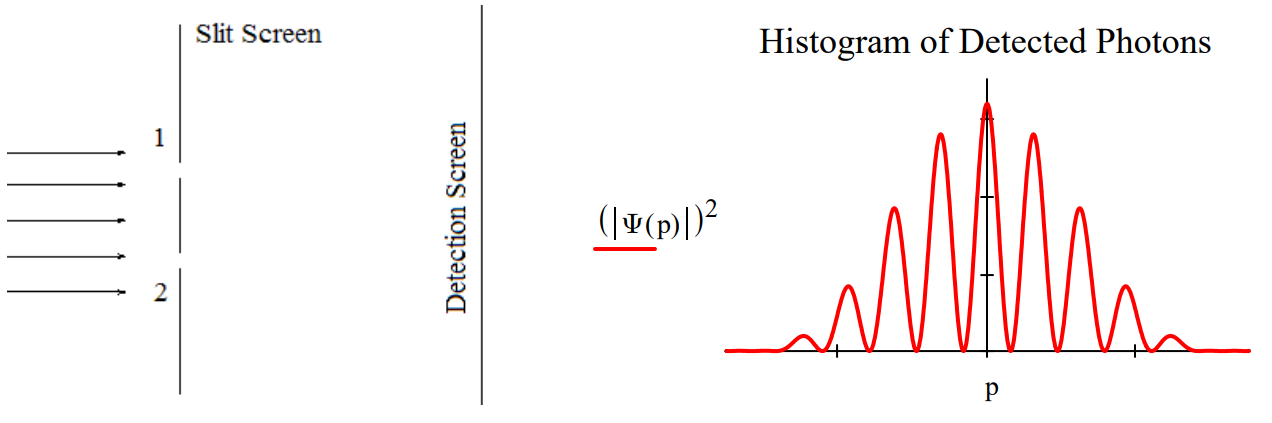
This tutorial examines the real reason which‐path information destroys the double‐slit diffraction pattern and how the so‐called ʺquantum eraserʺ restores it. The wave function for a photon illuminating the slit screen is written as a superposition of the photon being present at both slits simultaneously. The double‐slit diffraction pattern is calculated by projecting this superposition into momentum space. This is a Fourier transform for which the mathematical details can be found in the Appendix.
\[
| \Psi \rangle=\frac{1}{\sqrt{2}}[ |x_{1}\rangle+| x_{2} \rangle ] \qquad \Psi(p)=\langle p | \Psi\rangle=\frac{1}{\sqrt{2}}[\langle p | x_{1}\rangle+\langle p | x_{2}\rangle]
\nonumber \]
Attaching polarizers to the slits creates an entangled superposition of the photon being at slit 1 with vertical polarization and at slit 2 with horizontal polarization. This leads to the following momentum distribution at the detection screen. The interference fringes have disappeared leaving a single‐slit diffraction pattern.
\[
| \Psi^{\prime} \rangle=\frac{1}{\sqrt{2}}[ |x_{1}\rangle | V \rangle+| x_{2} \rangle | H \rangle ] \qquad \Psi^{\prime}(p)=\langle p | \Psi^{\prime}\rangle=\frac{1}{\sqrt{2}}[\langle p | x_{1}\rangle | V\rangle+\langle p | x_{2}\rangle | H \rangle ]
\nonumber \]
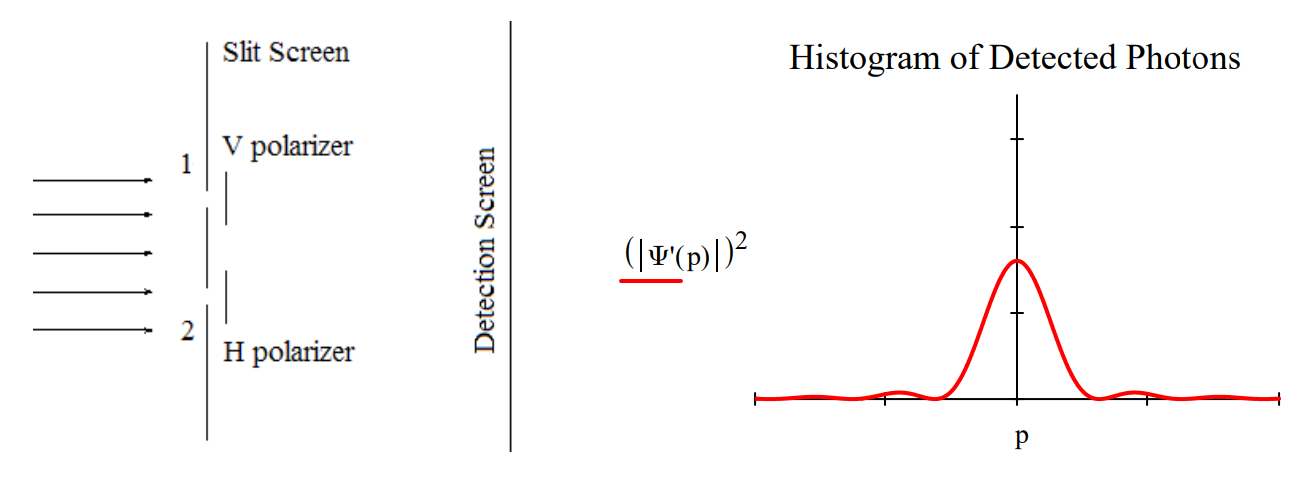
The usual explanation for this effect is that it is now possible to know which slit the photons went through, and that such knowledge destroys the interference fringes because the photons are no longer in a superposition of passing through both slits, but rather a mixture of passing through one slit or the other.
However, a better explanation is that the superposition persists with orthogonal polarization tags, and because of this the interference (cross) terms in the momentum distribution, \(| \Psi^{ʹ} (p)|^{2}\), vanish leaving a pattern at the detection screen which is the sum of two single‐slit diffraction patterns, one from the upper slit and the other from the lower slit.
That this is a reasonable interpretation is confirmed when a so‐called quantum eraser, a polarizer (D) rotated clockwise by 45 degrees relative to the vertical, is placed before the detection screen.
\[
\Psi^{\prime \prime}(p)=\langle D | \Psi^{\prime}(p)\rangle=\frac{1}{\sqrt{2}}[\langle p | x_{1}\rangle\langle D | V\rangle+\langle p | x_{2}\rangle\langle D | H\rangle]=\frac{1}{2}[\langle p | x_{1}\rangle+\langle p | x_{2}\rangle]
\nonumber \]
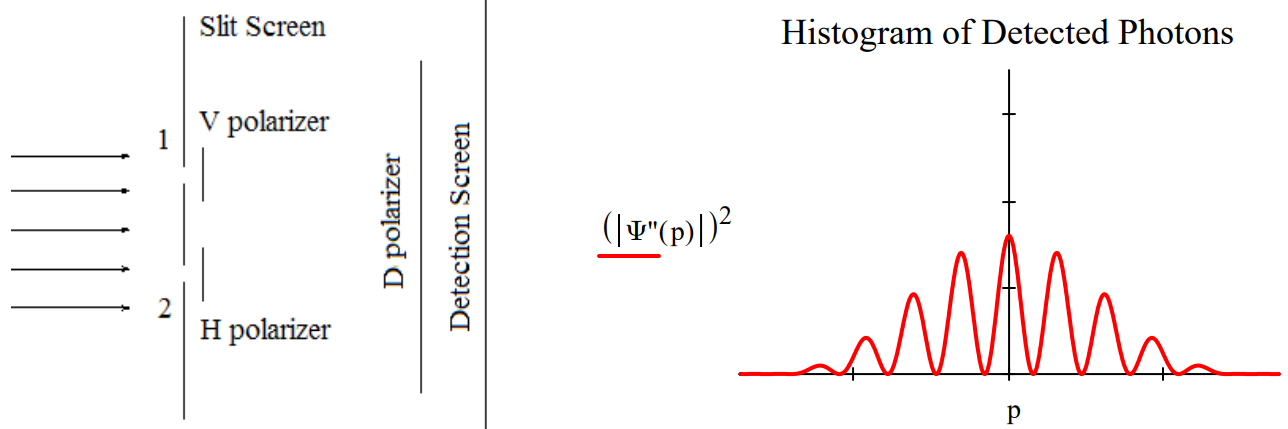
The diagonal polarizer is called a quantum eraser because it appears to restore the interference pattern lost because of the which‐path information provided by the V/H polarizers. However, it is clear from this analysis that the diagonal polarizer doesnʹt actually erase, it simply passes the diagonal component of \(| \Psi^{'} \rangle\) which then shows an attenuated (by half) version of the original interference pattern produced by \(| \Psi \rangle\).
Placing an anti‐diagonal polarizer (rotated counterclockwise by 45 degrees relative to the vertical) before the detection screen causes a 180 degree phase shift in the restored interference pattern.
\[
\Psi^{\prime \prime}(p)=\langle A | \Psi^{\prime}(p)\rangle=\frac{1}{\sqrt{2}}[\langle p | x_{1}\rangle\langle A | V\rangle+\langle p | x_{2}\rangle\langle A | H\rangle]=\frac{1}{2}[\langle p | x_{1}\rangle-\langle p | x_{2}\rangle]
\nonumber \]
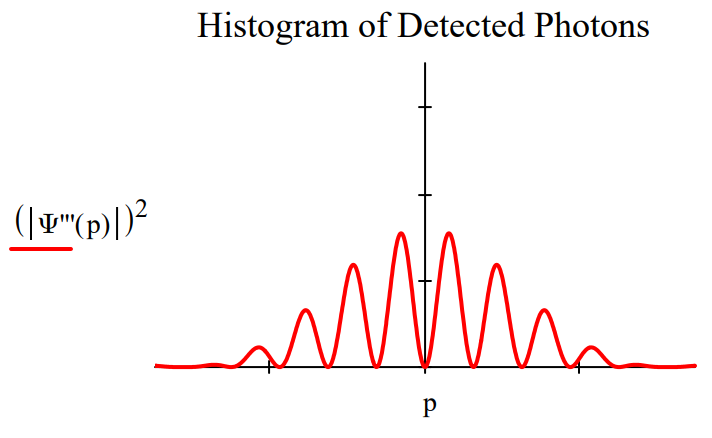
This phase shift is inconsistent with any straightforward explanation based on the concept of erasure of which‐path information. Erasure implies removal of which‐path information. If which‐path information has been removed shouldnʹt the original interference pattern be restored without a phase shift?
- Appendix:
-
The V/H polarization which‐path tags and the D/A polarization ʺerasersʺ in vector format:
\[
| \mathrm{V} \rangle=\left( \begin{array}{l}{1} \\ {0}\end{array}\right) | \mathrm{H} \rangle=\left( \begin{array}{l}{0} \\ {1}\end{array}\right) \qquad | \mathrm{D} \rangle=\frac{1}{\sqrt{2}} \left( \begin{array}{l}{1} \\ {1}\end{array}\right) | \mathrm{A} \rangle=\frac{1}{\sqrt{2}} \left( \begin{array}{c}{1} \\ {-1}\end{array}\right) \\ \langle\mathrm{D} | \mathrm{H}\rangle=\langle\mathrm{A} | \mathrm{V}\rangle=\langle\mathrm{A} | \mathrm{v}\rangle=\frac{1}{\sqrt{2}}\langle\mathrm{A} | \mathrm{H}\rangle=-\frac{1}{\sqrt{2}}
\nonumber \]For infinitesimally thin slits the momentum‐space wave function is
\[
\Psi(p)=\langle p | \Psi\rangle=\frac{1}{\sqrt{2}}[\langle p | x_{1}\rangle+\langle p | x_{2}\rangle]=\frac{1}{\sqrt{2}}\left[\frac{1}{\sqrt{2 \pi}} \exp \left(-i p x_{1}\right)+\frac{1}{\sqrt{2 \pi}} \exp \left(-i p x_{2}\right)\right]
\nonumber \]Assuming a slit width \(\delta\) the calculations of \(\Psi\)(p), \(\Psi^{ʹ}\)(p), \(\Psi^{"}\)(p) and \(\Psi^{"ʹ}\)(p) are carried out as follows:
Position of first slit: \(x_{1} \equiv 0\)
Position of second slit: \(x_{2} \equiv 1\)
Slit width: \(\delta \equiv 0.2\)
\[
\Psi(\mathrm{p}) \equiv \frac{1}{\sqrt{2}} \left[ \int_{x_{1}-\frac{\delta}{2}}^{x_{1}+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-i \cdot p \cdot x) \cdot \frac{1}{\sqrt{\delta}} d x +\int_{x_{2}-\frac{\delta}{2}}^{x_{2}+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-i \cdot p \cdot x) \cdot \frac{1}{\sqrt{\delta}} d x \right]
\nonumber \]For \(\Psi^{ʹ}\)(p) the V/H polarization which‐path tags are added to the two terms of \(\Psi\)(p)
\[
\Psi^{\prime}(\mathrm{p}) \equiv \frac{1}{\sqrt{2}} \left[ \int_{x_{1}-\frac{\delta}{2}}^{x_{1}+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-i \cdot p \cdot x) \cdot \frac{1}{\sqrt{\delta}} d x \cdot \left( \begin{array}{l}{1} \\ {0}\end{array}\right) \\ +\int_{x_{2}-\frac{\delta}{2}}^{x_{2} +\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-i \cdot p \cdot x) \cdot \frac{1}{\sqrt{\delta}} d x \cdot \left( \begin{array}{l}{0} \\ {1}\end{array}\right) \right]
\nonumber \]\(\Psi^{"}(p) is the projection of \(\Psi^{ʹ}\)(p) onto a diagonal polarizer <D|.
\[
\Psi^{\prime \prime}(p) \equiv \frac{1}{\sqrt{2}} \cdot \left( \begin{array}{c}{1} \\ {1}\end{array}\right)^{\mathrm{T}} \cdot \Psi^{\prime}(\mathrm{p})
\nonumber \]\(\Psi^{"'}\)(p) is the projection of \(\Psi^{ʹ}\)(p) onto an anti‐diagonal polarizer <A|.
\[
\Psi^{m}(\mathrm{p}) \equiv \frac{1}{\sqrt{2}} \cdot \left( \begin{array}{c}{1} \\ {-1}\end{array}\right)^{\mathrm{T}} \cdot \Psi^{\prime}(\mathrm{p})
\nonumber \]Rewriting \(\Psi^{ʹ}\)(p) in terms of |D> and |A> clearly shows the origin of the phase difference between the \(\left(\left|\Psi^{\prime \prime}(p)\right|\right)^{2}\) and \(\left(\left|\Psi^{\prime \prime \prime}(p)\right|\right)^{2}\) interference patterns.
\[
\Psi^{\prime}(p)=\langle p | \Psi^{\prime}\rangle=\frac{1}{2}[(\langle p | x_{1}\rangle+\langle p | x_{2}\rangle) | D\rangle+(\langle p | x_{1}\rangle-\langle p | x_{2}\rangle) | A \rangle ]
\nonumber \]
A Brief Analysis of Deutsch's Problem
A certain function of x maps {0,1} to {0,1}. The four possible outcomes of the evaluation of f(x) are given in tabular form.
\[\begin{pmatrix} x & ' & 0 & 1 & ' & 0 & 1 & ' & 0 & 1 & ' & 0 & 1 \\ f(x) & ' & 0 & 0 & ' & 1 & 1 & ' & 0 & 1 & ' & 1 & 0 \end{pmatrix} \nonumber \]
The circuit shown below yields the result given in the right most section of the table. In other words, f(x) is a balanced function, because \(f(0) \neq f(1)\), as is the result immediately to its left. The results in the first two sections are labelled constant because \(f(0) = f(1)\).
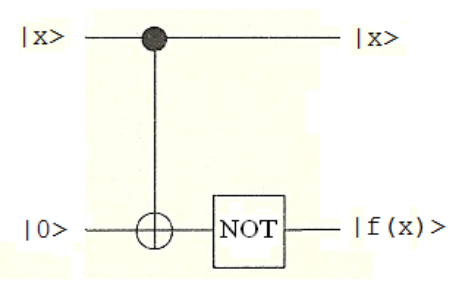
where
\[
| 0 \rangle=\left( \begin{array}{l}{1} \\ {0}\end{array}\right) \qquad | 1 \rangle=\left( \begin{array}{l}{0} \\ {1}\end{array}\right)
\nonumber \]
From the classical perspective, if the question (as asked by Deutsch) is whether f(x) is constant or balanced then one must calculate both f(0) and f(1) to answer the question. Deutsch pointed out that quantum superpositions and the interference effects between them allow the answer to be given with one pass through the following modified version of the circuit.
\[\begin{array} a | 0 \rangle & \rhd & \mathrm{H} & \cdots & \cdot & \cdots & \mathrm{H} & \rhd & \text{measure}\; \frac{| 0 \rangle \text{constant}}{| 1 \rangle \text{balanced}} \\ \; & \; & \; & \; & | & \; & \; & \; & \; \\ | 1 \rangle & \rhd & \mathrm{H} & \cdots & \oplus & \mathrm{NOT} & \cdots & \; & \; \end{array} \nonumber \]
An algebraic analysis of the operation of Deutsch's algorithm is now provided. Truth tables for H, CNOT, NOT and the identity are provided in the Appendix.
\[
| 0 \rangle | 1 \rangle=| 01 \rangle \\ \mathrm{H} \otimes \mathrm{H} \\ \frac{1}{\sqrt{2}}[ |0\rangle+| 1 \rangle ] \frac{1}{\sqrt{2}}[ |0\rangle-| 1 \rangle ]=\frac{1}{2}[ |00\rangle-| 01 \rangle+| 10 \rangle-| 11 \rangle ] \\ \mathrm{CNOT} \\ \frac{1}{2}[ |00\rangle-| 01 \rangle+| 1 1 \rangle-| 10 \rangle ]=\frac{1}{2}( |0\rangle-| 1 \rangle )( |0\rangle-| 1 \rangle ) \\ \mathrm{I} \otimes \mathrm{NOT} \\ \frac{1}{2}[( |0\rangle-| 1\rangle )( |1\rangle-| 0 \rangle ) ] \\ \mathrm{H} \otimes \mathrm{I} \\ | 1 \rangle \frac{1}{\sqrt{2}}( |1\rangle-| 0 \rangle )
\nonumber \]
The top wire contains |1 > indicating the function is balanced.
- Appendix:
-
Identity
\[
\left( \begin{array}{lll}{0} & {\text { to }} & {0} \\ {1} & {\text { to }} & {1}\end{array}\right)
\nonumber \]NOT
\[
\left( \begin{array}{lll}{0} & {\text { to }} & {1} \\ {1} & {\text { to }} & {0}\end{array}\right)
\nonumber \]CNOT
\[
\left( \begin{array}{ccc}{00} & {\text { to }} & {00} \\ {01} & {\text { to }} & {01} \\ {10} & {\text { to }} & {11} \\ {11} & {\text { to }} & {10}\end{array}\right)
\nonumber \]Hadamard operation
\[\left[ \begin{matrix} 0 & ' & H & ' & \frac{1}{\sqrt{2}} \cdot (0+1) & ' & H & ' & 0 \\ 1 & ' & H & ' & \frac{1}{\sqrt{2}} \cdot (0-1) & ' & H & ' & 1 \end{matrix} \right] \nonumber \]
The Hadamard operation is a simple example of a discrete Fourier transform. In other words, the final step of Deutsch's algorithm is to carry out a Fourier transform on the input wire. This also occurs on the input wires in Grover's search algorithm, Simon's query algorithm and Shor's factorization algorithm. These are other types of calculations in which quantum superpositions and interference effects enable a quantum computer to outperform a classical computer.

