1.4: Atomic and Molecular Stability
- Page ID
- 135318
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)I apologize for the considerable overlap in the following, but it does provide some additional interpretive graphics. It also contains references to the publications of Slater and Ruedenberg.
The Chemical Bond According to Slater and Ruedenberg
John Slater pioneered the use of the virial theorem in interpreting the chemical bond in a benchmark paper published in the inaugural volume of the Journal of Chemical Physics (1). This early study indicated that electron kinetic energy played an important role in bond formation. Thirty years later Klaus Ruedenberg and his collaborators published a series of papers (2,3,4) detailing the crucial role that kinetic energy plays in chemical bonding, thereby completing the project that Slater started. This Mathcad worksheet recapitulates Slater's use of the virial theorem in studying chemical bond formation and summarizes Ruedenberg final analysis.
Equation [1] gives the virial theorem for a diatomic molecule as a function of internuclear separation, while Equation \ref{2} is valid at the energy minimum.
\[1 \cdot T(R) + V(R) = -R \frac{d}{dR} E(R) \label{1} \]
\[E(R_{e}) = \frac{v(R_{e})}{2} = -T(R_{e}) \label{2} \]
At non-equilibrium values for the internuclear separation the virial equation can be used, with \(E = T + V\), to obtain equations for the kinetic and potential energy as a function of the inter-nuclear separation.
\[T(R) : = -E(R)-R \frac{d}{dR} E(R) \label{3} \]
\[V(R) : = 2 E(R) + R \frac{d}{dR} E(R) \label{4} \]
Thus, if \(E(R)\) is known one can calculate \(T(R)\) and \(V(R)\) and provide a detailed energy profile for the formation of a chemical bond. \(E(R)\) can be provided from spectroscopic data or from ab initio quantum mechanics. In this examination of the chemical bond we employ the empirical approach and use spectroscopic data for the hydrogen molecule to obtain the parameters (highlighted below) for a model of the chemical bond based on the Morse function (5). However, it should be noted that quantum mechanics tells the same story and yields an energy profile just like that shown in the following figure.
\(R \equiv 30, 30.2 \ldots 400 \quad D_{e} \equiv 0.761 \quad \beta = 0.0193 \quad R_{e} \equiv 74.1\)
\[E(R) \equiv [D_{e} (1- \exp [- \beta (R - R_{e})])^{2} - D_{e}] \nonumber \]
The dissociation energy, De, is given in atta (10-18) joules, the internuclear separation in picometers, and the constant \(\beta\) in inverse picometers.
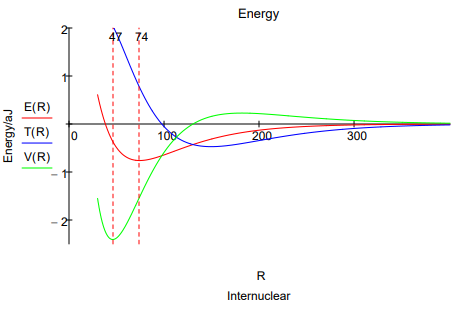
This energy profile shows that as the internuclear separation decreases, the potential energy rises, falls, and then rises again. The kinetic energy first decreases and then increases at about the same internuclear distance that the potential energy begins to decrease.
As the molecular orbital is formed at large \(R\) constructive interference between the two overlaping atomic orbitals draws electron density away from the nuclear centers into the internuclear region. The potential energy rises as electron density is drawn away from the nuclei, but the total energy decreases because of a larger decrease in kinetic energy due to charge delocalization. Thus a decrease in kinetic energy funds the initial build up of charge between the nuclei that we normally associate with chemical bond formation.
Following this initial phase, at an internuclear separation of about 180 pm the potential energy begins to decrease and the kinetic energy increases, both sharply (eventually), while the total energy continues to decrease gradually. This is an atomic effect, not a molecular one as Ruedenberg so clearly showed. The initial transfer of charge away from the nuclei and into the bond region allows the atomic orbitals to contract significantly (\(\alpha\) increases) causing a large decrease in potential energy because the electron density has moved, on average, closer to the nuclei. The kinetic energy increases because the orbitals are smaller and kinetic energy increases inversely with the square of the orbital radius.
An energy minimum is reached while the potential energy is still in a significant decline (6), indicating that kinetic energy is the immediate cause of a stable bond and the molecular ground state in H2. The final increase in potential energy which is due mainly to nuclear-nuclear repulsion, and not electron-electron repulsion, doesn't begin until the internuclear separation is less than 50 pm, while the equilibrium bond length is 74 pm . Thus the common explanation that an energy minimum is reached because of nuclear-nuclear repulsion does not have merit.
The H2 ground state, E = -0.761 aJ, is reached at an internuclear separation of 74 pm (1.384 a0). In light of the previous arguments it is instructive to partition the total H2 electron density into atomic and molecular contributions. Each electron is in a molecular orbital which is a linear combination of hydrogenic 1s orbitals, as is shown below.
\[\Psi_{mo} = \frac{\Psi_{1sa} + \Psi_{1sb}}{\sqrt{2 + 2S_{ab}}} \quad where \quad \Psi_{1sa} = \sqrt{\frac{\alpha^{3}}{\pi}} \exp (- \alpha r_{a}) \quad \Psi_{1sb} = \sqrt{\frac{\alpha^{3}}{\pi}} \exp (- \alpha r_{b}) \nonumber \]
The total electron density is therefore 2\(\Psi_{MO}^{2}\). The atomic, or non-bonding, electron density is given by the following equation, which represents the electron density associated with two non-interacting atomic orbitals.
\[\rho_{n} = 2 \left( \Bigg| \dfrac{\Psi_{1sa} + i \Psi_{1sb}}{\sqrt{2}} \Bigg| \right)^{2} = \Psi_{1sa}^{2} + \Psi_{1sb}^{2} \nonumber \]
Clearly, the bonding electron density must be the difference between the total electron density and the non-bonding, or atomic, electron density.
\[\rho_{b} = \Psi_{MO}^{2} - \rho_{n} = \rho_{t} - \rho_{n} \nonumber \]
These three terms are plotted along the bond axis in the figure below. Alpha is the optimum orbital scale factor, Sab is the overlap integral, and R is the equilibrium internuclear distance in atomic units.
\(\alpha : = 1.197 \quad S_{ab} : = 0.681 \quad R : = 1.384 \quad y : = 0 \quad z : = 0 \quad x : = -3, -2.99 \ldots 5\)
\[\rho_{t} (\alpha, x, y, z) : = \frac{\frac{\alpha^{3}}{\pi} \bigg[ \exp (- \alpha \sqrt{x^{2} + y^{2} + z^{2}}) + \exp (- \alpha \sqrt{(x - R)^{2} + y^{2} + z^{2}}) \bigg]^{2}}{1 + S_{ab}} \nonumber \]
\[\rho_{n} (\alpha, x, y, z) : = \frac{\alpha^{3}}{\pi} \bigg[ \exp (-2 \alpha \sqrt{x^{2} + y^{2} + z^{2}}) + \exp (-2 \alpha \sqrt{(x-R)^{2} + y^{2} + z^{2}}) \bigg] \nonumber \]
\[\rho_{b} (\alpha, x, y, z) : = \rho_{t} (\alpha, x, y, z) - \rho_{n} (\alpha, x, y, z) \nonumber \]
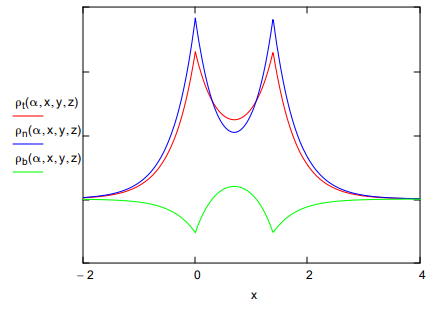
The bonding electron density illustrates that constructive interference accompanying atomic orbital overlap transfers charge from the nuclei into the internuclear region, while the non-bonding density clearly shows the subsequent atomic orbital contraction which draws some electron density back toward the nuclei.
Literature cited:
- Slater, J. C. J. Chem. Phys. 1933, 1, 687-691.
- Ruedenberg, K. Rev. Mod. Phys. 1962, 34, 326-352.
- Feinberg, M. J.; Ruedenberg, K. J. Chem. Phys. 1971, 54, 1495-1511; 1971, 55, 5804-5818.
- Feinberg, M. J.; Ruedenberg, K.; Mehler, E. L. Adv. Quantum Chem. 1970, 5, 27-98.
- McQuarrie, D. A.; Simon, J. D. Physical Chemistry: A Molecular Approach, University Science Books, Sausalito, CA, 1997, p. 165.
- Slater, J. C. Quantum Theory of Matter, Krieger Publishing, Huntington, N.Y., 1977, pp. 405-408.
- Rioux, F. The Chemical Educator, 1997, 2, No. 6.
I close with a rather mystical description of the chemical bond by Charles A. Coulson, the author of Valence, an influential monograph on the chemical bond published in 1952.
Sometimes it seems to me that a bond between two atoms has become so real, so tangible, so friendly, that I can almost see it. Then I awake with a little shock, for a chemical bond is not a real thing. It does not exist. No one has ever seen one. No one ever will. It is a figment of our own imagination.... Here is a strange situation. The tangible, the real, the solid, is explained by the intangible, the unreal, the purely mental.
Addendum: The Bohr Model of Atomic and Molecular Stability
The purpose of this study was to outline the success of quantum mechanics in explaining the stability and structure of matter. But quantum mechanics didn’t emerge out of a vacuum; it had a precursor – the Bohr model. So I thought it appropriate to take a brief look at that precursor and present its explanation of atomic and molecular stability.
My starting point (for the development of the Bohr model) was not at all the idea that an atom is a small-scale planetary system and as such governed by the laws of astronomy. I never took things as literally as that. My starting point was rather the stability of matter, a pure miracle when considered from the standpoint of classical physics. -Niels Bohr
All matter consists of elements that are made up of electrons, protons and neutrons. Given that the electron and the proton have opposite charges and therefore are attracted to one another provides the problem that classical physics has in explaining the stability of matter. What keeps these oppositely charged building blocks apart? There is no more fundamental question in science and Bohr was the first to attempt an explanation of atomic stability by creating, by fiat, the necessary rudimentary quantum mechanical concepts.
We begin with the Bohr model for the simplest element, the hydrogen atom. In the following tutorial the Bohr model is enriched with de Broglie’s hypothesis of wave properties for the electron. This allows the reinterpretation of some of the apparently arbitrary features of Bohr’s initial atomic model.
A deBroglie‐Bohr Model for the Hydrogen Atom
The 1913 Bohr model of the hydrogen atom was replaced by Schrödingerʹs wave mechanical model in 1926. However, Bohrʹs model is still profitably taught today because of its conceptual and mathematical simplicity, and because it introduced a number of key quantum mechanical ideas such as the quantum number, quantization of observable properties, quantum jump and stationary state.
Bohr calculated the manifold of allowed electron energies by balancing the mechanical forces (centripetal and electron‐nucleus) on an electron executing a circular orbit of radius R about the nucleus, and then arbitarily quantizing its angular momentum. Finally by fiat he declared that the electron was in a non‐radiating stationary state because an orbiting (accelerating) charge radiates energy and will collapse into the oppositely charge nucleus. In 1924 de Broglie postulated wave‐particle duality for the electron and other massive particles, thereby providing the opportunity to remove some of the arbitariness from Bohrʹs model. For example, an electron possessing wave properties is subject to constructive and destructive interference. As will be shown this leads naturally to quantization of electron momentum and kinetic energy, and consequently a manifold of allowed energy states for the electron relative to the nucleus.
The de Broglie‐Bohr model of the hydrogen atom presented here treats the electron as a particle on a ring with wave‐like properties.
| $$\lambda = \frac{h}{m_{e} \nu}$$ | de Broglieʹs hypothesis that matter has wave‐like properties |
| $$n \lambda = 2 \pi r$$ | The consequence of de Broglieʹs hypothesis; an integral number of wavelengths must fit within the circumference of the orbit. This introduces the quantum number which can have values 1,2,3,... The n = 4 electron state is shown below. |
| $$m_{e} \nu = \frac{n \cdot h}{2 \pi r}$$ | Substitution of the first equation into the second equation reveals that momentum is quantized. |
| $$T = \frac{1}{2} m_{e} \nu^{2} = \frac{n^{2} h^{2}}{8 \pi^{2} m_{e} r^{2}}$$ | If momentum is quantized, so is kinetic energy. |
| $$E = T + V = \frac{n^{2} h^{2}}{8 \pi^{2} m_{e} r^{2}} - \frac{e^{2}}{4 \pi \epsilon_{0} r}$$ | Which means that total energy is quantized. The second term is the electron‐proton electrostatic potential energy. |
The quantum mechanical interpretation of these ʺBohr orbitsʺ is that they are stationary states. In spite of the fact that we use the expression kinetic energy, which implies electron motion, there is no motion. The electron occupies the orbit as a particle‐wave, it is not orbiting the nucleus. If it was orbiting in a classical sense it would radiate energy and quickly collapse into the nucleus. Clearly the stability of matter requires the quantum mechanical version of kinetic energy.
The ground state energy and orbit radius of the electron in the hydrogen atom is found by plotting the energy as a function of the orbital radius. The ground state is the minimum in the total energy curve. Naturally calculus can be used to obtain the same information by minimizing the energy with respect to the orbit radius. However, the graphical method has the virtue of illuminating the issue of atomic stability.
| Fundamental constants: electron charge, electron mass, Planckʹs constant, vacuum permitivity. | \(e : = 1.6021777 \times 10^{-19}\; coul\) | \(m_{e} : = 9.10939 \times 10^{-31}\; kg\) |
| \(h : = 6.62608 \times 10^{-34}\; joule \cdot sec\) | \(\epsilon_{0} : = 8.85419 \times 10^{-12}\; \frac{coul^{2}}{joule \cdot m}\) |
| Quantum number and conversion factor between meters and picometers and joules and attojoules. | \(n : = 1 \qquad pm : = 10^{-12}\; m \qquad ajoule : = 10^{-18}\; joule\) |
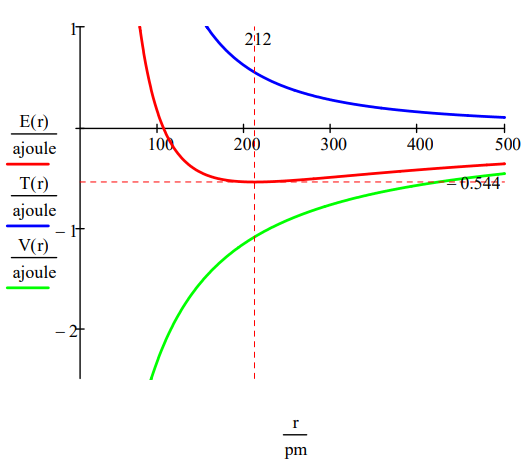
\[r : = 20, 20.5 \ldots 500\; pm \quad T(r) : = \frac{n^{2} h^{2}}{8 \pi^{2} m_{e} r^{2}} \quad V(r) : = \frac{e^{2}}{4 \pi \epsilon_{0} r} \quad E(r) : = T(r) + V(r) \nonumber \]
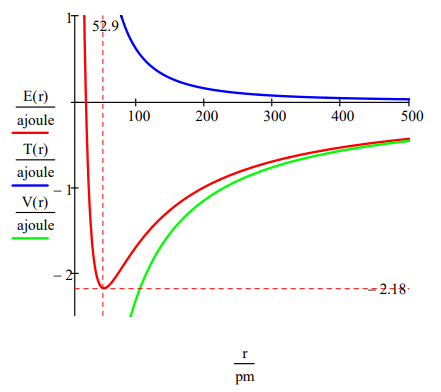
This figure shows that atomic stability involves a balance between potential and kinetic energy. The electron is drawn toward the nucleus by the attractive potential energy interaction (~ ‐1/R), but is prevented from collapsing into the nucleus by the extremely large kinetic energy (~1/R2) associated with small orbits.
As shown below, the graphical approach can also be used to find the electronic excited states.
\[n : = 2 \quad T(r) : = \frac{n^{2} h^{2}}{8 \pi^{2} m_{e} r^{2}} \quad V(r) : = - \frac{e^{2}}{4 \pi \epsilon_{0} r} \quad E(r) : = T(r) + V(r) \nonumber \]
As mentioned earlier the manifold of allowed electron energies can also be obtained by minimizing the energy with respect to the orbit radius. This procedure yields,
\[E_{n} = - \frac{m_{e} e^{4}}{2(4 \pi \epsilon_{0})^{2} \hbar^{2}} \frac{1}{n^{2}} \quad and \quad r_{n} = \frac{4 \pi \epsilon_{0} \hbar^{2}}{m_{e} e^{2}} n^{2} \nonumber \]
The Bohr model gives correct results for any one-electron atomic atom or ion. The following tutorial shows that it is also accurate when applied to the rather esoteric and short-lived hydrogen atom analog positronium, in which the proton is replaced the positron, the electron’s antiparticle.
A deBroglie-Bohr Model for Positronium
Positronium is a metastable bound state consisting of an electron and its positron antiparticle. In other words it might be thought of as a hydrogen atom in which the proton is replaced by a positron. Naturally it decays quickly after formation due to electron-positron annihilation. However, it exists long enough for its ground state energy, -0.25 Eh, to be determined. The purpose of this tutorial is to calculate this value using the Bohr model for positronium shown below.
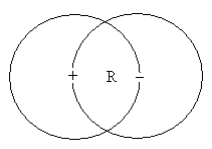
The electron occupies a circular orbit of radius R which has a positron at its center. Likewise the positron occupies a circular orbit of radius R which has an electron at its center. Occupies has been emphasized to stress that there is no motion, no orbiting. Both particles are behaving as waves (this is the meaning of wave-particle duality) occupying the orbit. As waves they are subject to interference, and to avoid destructive interference the wavelength for the ground state is one orbit circumference.
\[\lambda = 2 \pi R \nonumber \]
Introducing the de Broglie relationship between wavelength and momentum, \(\lambda = \frac{h}{p}\), yields the following expression for momentum in atomic units (h = 2\(\pi\)).
\[p = \frac{h}{2 \pi R} = \frac{1}{R} \nonumber \]
In atomic units me = mp = 1. Therefore, the kinetic energy of each particle is,
\[T = \frac{p^{2}}{2m} = \frac{1}{2R^{2}} \nonumber \]
The total energy of positronium is the sum of electron and positron kinetic energies and their coulombic potential energy.
\[E = T_{e} + T_{p} + V_{ep} = \frac{1}{2R^{2}} + \frac{1}{2R^{2}} - \frac{1}{R} = \frac{1}{R^{2}} - \frac{1}{R} \nonumber \]
Energy minimization with respect to the electron-positron distance R yields the following result.
\[\frac{d}{dR} \left(\dfrac{1}{R^{2}} - \dfrac{1}{R}\right) = 0 \quad \text{solve,}\; R \rightarrow 2 \nonumber \]
The optimum R value yields a ground state energy of -0.25 Eh, in agreement with experiment.
\[E = \frac{1}{R^{2}} - \frac{1}{R} \quad \text{substitute,}\; R = 2 \rightarrow E = - \frac{1}{4} \nonumber \]
Including the symbols for mass in the kinetic energy contributions facilitates the introduction of the concept of effective mass of the composite system.
\[T = \frac{1}{2 m_{e} R^{2}} + \frac{1}{2m_{p} R^{2}} = \frac{1}{2R^{2}} \left(\dfrac{1}{m_{e}} + \dfrac{1}{m_{p}}\right) = \frac{1}{2R^{2}} \left(\dfrac{m_{e} + m_{p}}{m_{e} \cdot m_{p}} \right) = \frac{1}{2 \mu_{ep} R^{2}} \nonumber \]
\[\mu_{ep} = \frac{m_{e} \cdot m_{p}}{m_{e} + m_{p}} = \frac{1 \cdot 1}{1 + 1} = \frac{1}{2} \nonumber \]
The positronium energy minimum can also be located graphically.
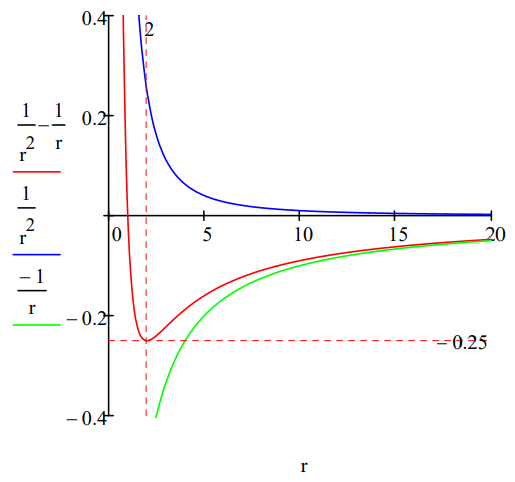
Plotting kinetic and potential energy along with total energy reveals that a ground state is achieved because beginning at R = 2, the kinetic energy is approaching positive infinity more quickly than the potential energy is approaching negative infinity.
After reviewing the Bohr model for the hydrogen atom, the following tutorial outlines Bohr’s model for the hydrogen molecule. It shows that it yields plausible values for bond energy and bond length.
Extracting Atomic and Molecular Parameters From the de Broglie‐Bohr Model of the Atom
The 1913 Bohr model of the hydrogen atom was replaced by Schrödingerʹs wave mechanical model in 1926. However, Bohrʹs model is still profitably taught today because of its conceptual and mathematical simplicity, and because it introduced a number of key quantum mechanical ideas such as the quantum number, quantization of observable properties, quantum jump and stationary state. In addition it provided realistic values for such parameters as atomic and molecular size, electron ionization energy, and molecular bond energy.
In his ʺplanetaryʺ model of the hydrogen atom Bohr began with a Newtonian analysis of the electron executing a circular orbit of radius R about a stationary nucleus, and then arbitrarily quantized the electronʹs angular momentum. Finally, by fiat he declared that the electron was in a non‐radiating stationary state because an orbiting (accelerating) charge radiates energy and will collapse into the oppositely charge nucleus.
In 1924 de Broglie postulated wave‐particle duality for the electron and other massive particles, thereby providing the opportunity to remove some of the arbitrariness from Bohrʹs model. For example, an electron possessing wave properties is subject to constructive and destructive interference. As will be shown this leads naturally to quantization of electron momentum and kinetic energy, and consequently to a stable ground state for the hydrogen atom.
The de Broglie‐Bohr model of the hydrogen atom presented here treats the electron as a particle on a ring with wave‐like properties. The key equation is wave‐particle duality as expressed by the de Broglie equation. The particle concept momentum and the wave concept \(\lambda\) are joined in a reciprocal relationship mediated by the ubiquitous Planckʹs constant.
\[p = \frac{h}{\lambda} \nonumber \]
This equation will be used with the Bohr model of the hydrogen atom to explain atomic stability and to generate estimates of atomic size and electron binding energy in the atom.
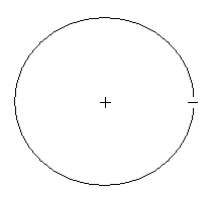
In the de Broglie version of the Bohr hydrogen atom we say that the electron occupies a ring of radius R. It is not orbiting the nucleus, it is behaving as a stationary wave. In order to avoid self‐interference the following wavelength restriction must be obeyed for the ground state of the hydrogen atom.
\[\lambda = 2 \pi R \nonumber \]
When combined with the de Broglie equation it reveals the following restriction on the electronʹs particle property, linear momentum.
\[p = \frac{h}{2 \pi R} \nonumber \]
This means there is also a restriction on the electronʹs kinetic energy. Use of this equation in the classical expression for kinetic energy yields the quantum mechanical kinetic energy or more accurately electron confinement energy
\[T = \frac{p^{2}}{2m} = \frac{h^{2}}{8 \pi^{2} mR^{2}} = \frac{1}{2R^{2}} \nonumber \]
In this equation we have moved from the classical definition of kinetic energy to the quantum mechanical version expressed on the right in atomic units.
\[\frac{h}{2 \pi} = m = e = 4 \pi \epsilon_{0} = 1 \nonumber \]
The electrostatic potential energy retains its classical definition in quantum mechanics.
\[V = \frac{-e^{2}}{4 \pi \epsilon_{0} R} = \frac{-1}{R} \nonumber \]
The total electron energy, EH(R) = T(R) + V(R), is now minimized with respect to the ring or orbit radius, the only variational parameter in the model. The total energy, and kinetic and potential energy are also displayed as a function of ring radius.
\[R : = 0.5 \quad E_{H} (R) : = \frac{1}{2R^{2}} - \frac{1}{R} \quad R : = \text{Minimize} (E_{H}, R) \quad R = 1.000 \quad E_{H}(R) = -0.500 \nonumber \]
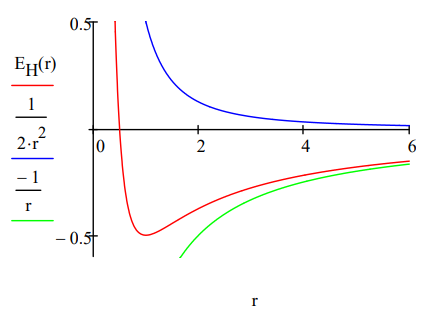
From this simple model we learn that it is the wave nature of the electron that explains atomic stability. The electronʹs ring does not collapse into the nucleus because kinetic (confinement) energy goes to positive infinity (~R‐2) faster than potential energy goes to negative infinity (~‐R‐1). This is seen very clearly in the graph. The ground state is due to the sharp increase in kinetic energy as the ring radius decreases. This is a quantum effect, a consequence of de Broglieʹs hypothesis that electrons have wave‐like properties. As Klaus Ruedenberg has written, ʺThere are no ground states in classical mechanics.ʺ
The minimization process above the figure provides the ground state ring radius and electron energy in atomic units, a0 and Eh, respectively. R = 1 a0 = 52.9 pm gives us the benchmark for atomic size. Tables of atomic and ionic radii carry entries ranging from approximately half this value to roughly five or six times it. The ground state (binding) energy, E = ‐0.5 Eh = ‐13.6 eV = ‐1312 kJ/mol, is the negative of the ionization energy. This value serves as a benchmark for how tightly electrons are held in atoms and molecules.
A more comprehensive treatment of the Bohr atom utilizing the restriction that an integral number of wavelengths must fit within the ring, n\(\lambda\) = 2\(\pi\)R , where n = 1, 2, 3, ... reveals a manifold of allowed energy states (‐0.5 Eh/n2) and the basis for Bohrʹs concept of the quantum jump which ʺexplainedʺ the hydrogen atom emission spectrum. Here for example is the n = 4 Bohr atom excited state.
Rudimentary estimates of some molecular parameters, the most important being bond energy and bond length, can be obtained using the following Bohr model for H2. The distance between the protons is D, the electron ring radius is R, and the bond axis is perpendicular to the plane of the ring
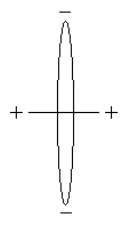
There are eight contributions to the total molecular energy based on this model: electron kinetic energy (2), electron‐proton potential energy (4), proton‐proton potential energy (1) and electron‐electron potential energy (1).
\[E_{H2} (R,D) : = \frac{1}{R^{2}} - \frac{4}{\sqrt{R^{2} + (\frac{D}{2})^{2}}} + \frac{1}{D} + \frac{1}{2R} \nonumber \]
Minimization of the energy with respect to ring radius and proton‐proton distance yields the following results.
\[D : = 2 \quad \begin{pmatrix} R \\ D \end{pmatrix} : = \text{Minimize} (E_{H2}, R,D) \quad \begin{pmatrix} R \\ D \end{pmatrix} = \begin{pmatrix} 0.953 \\ 1.101 \end{pmatrix} \quad E_{H2} (R,D) = -1.100 \nonumber \]
The H‐H bond energy is the key parameter provided by this analysis. We see that it predicts a stable molecule and that the energy released on the formation of H2 is 0.1 Eh or 263 kJ/mol, compared with the experimental value of 458 kJ/mol. The model predicts a H‐H bond length of 58 pm (D.52.9 pm), compared to the literature value of 74 pm. These results are acceptable given the primitive character of the model.
\[H + H = H_{2} \nonumber \]
\[\Delta E_{bond} : = E_{H2} (R,D) = -2 E_{H}(1) \quad \Delta E_{bond} = -0.100 \nonumber \]
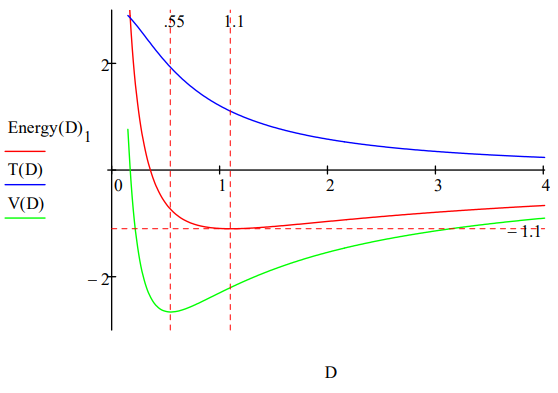
In addition to these estimates of molecular parameters, the model clearly shows that molecular stability depends on a balancing act between electron‐proton attraction and the ʺrepulsiveʺ character of electron kinetic energy. Just as in the atomic case, it is the 1/R2 dependence of kinetic (confinement) energy on ring radius that prevents molecular collapse under electron‐proton attraction. As the energy profile provided in the Appendix shows, the immediate cause of the molecular ground state is a rise in kinetic energy. Potential energy is still declining at this point and does not begin to rise until 0.55 a0, well after the ground state is reached at 1.10 a0.
Although the model is a relic from the early days of quantum theory it still has pedagogical value. Its mathematical simplicity clearly reveals the importance of the wave nature of matter, the foundational concept of quantum theory.
Two relatively recent appraisals of Bohrʹs models of atomic and molecular structure have been appeared in Physics Today:
- ʺNiels Bohr between physics and chemistry,ʺ by Helge Kragh, May 2013, 36‐41.
- ʺBohrʹs molecular model, a century later,ʺ by Anatoly Svidzinsky, Marlan Scully, and Dudley Herschbach, January 2014, 33‐39.
- Appendix:
-
\[R : = 0.1 \quad \text{Energy} : = -1 \quad Given\; \text{Energy} = E_{H2} (R,D) \quad \frac{d}{dR} E_{H2} (R,D) = 0 \quad \text{Energy(D) : = Find(R, Energy)} \nonumber \]
\[D : = 0.15, 0.16 \ldots 4 \quad T(D) : = \frac{1}{[Energy(D)_{0}]^{2}} \quad V(D) : = - \frac{4}{\sqrt{[Energy(D)_{0}]^{2} + (\frac{D}{2})^{2}}} + \frac{1}{D} + \frac{1}{2 \cdot \text{Energy}(D)_{0}} \nonumber \]
The examples presented in this addendum are based on classical pictures of the hydrogen atom, positronium, and the hydrogen molecule that have been moved in the quantum direction with de Broglie’s hypothesis of wave-particle duality for matter. Bohr and de Broglie are the early quantum theorists who cut a path for those who created modern quantum theory.

