31.3: The Spacing Between Lattice Planes Can Be Determined from X-Ray Diffraction Measurements
- Page ID
- 14575
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)X-ray crystallography is an instrumental technique used to determine the arrangement of atoms of a crystalline solid in three-dimensional space. This technique takes advantage of the interatomic spacing of most crystalline solids by employing them as a diffraction grating for x-ray light, which has wavelengths on the order of 1 angstrom (10-8 cm).
Introduction
In 1895, Wilhelm Rontgen discovered x- rays. The nature of x- rays, whether they were particles or electromagnetic radiation, was a topic of debate until 1912. If the wave idea was correct, researchers knew that the wavelength of this light would need to be on the order of 1 Angstrom (Å) (10-8 cm). Diffraction and measurement of such small wavelengths would require a grating with spacing on the same order of magnitude as the light.
In 1912, Max von Laue, at the University of Munich in Germany, postulated that atoms in a crystal lattice had a regular, periodic structure with interatomic distances on the order of 1 Å. Without having any evidence to support his claim on the periodic arrangements of atoms in a lattice, he further postulated that the crystalline structure could be used to diffract x-rays, much like a grating in an infrared spectrometer can diffract infrared light. His postulate was based on the following assumptions: the atomic lattice of a crystal is periodic, x- rays are electromagnetic radiation, and the interatomic distance of a crystal is on the same order of magnitude as x-ray light. Laue's predictions were confirmed when two researchers: Friedrich and Knipping, successfully photographed the diffraction pattern associated with the x-ray radiation of crystalline \(CuSO_4 \cdot 5H_2O\). The science of x-ray crystallography was born.
The arrangement of the atoms needs to be in an ordered, periodic structure for them to diffract the x-ray beams. A set of mathematical calculations is then used to produce a diffraction pattern that is characteristic of the particular arrangement of atoms in that crystal. X-ray crystallography remains to this day the primary tool used by researchers in characterizing the structure and bonding of many compounds.
Diffraction
Diffraction is a phenomenon that occurs when light encounters an obstacle. The waves of light can either bend around the obstacle or, in the case of a slit, can travel through the slits. The resulting diffraction pattern will show areas of constructive interference, where two waves interact in phase, and destructive interference, where two waves interact out of phase. Calculation of the phase difference can be explained by examining Figure \(\PageIndex{1}\) below.
In the figure above, two parallel waves are striking a grating at an angle \(\alpha_o\). The incident wave on the right travels farther than the one on the left by a distance of BD before reaching the grating. The scattered wave depicted below the gradient on the left, travels farther than the scattered wave on the right by a distance of AC. So the total path difference between the left wave and the right wave is AC - BD. To observe a wave of high intensity (one created through constructive interference), the difference AC - BD must equal an integer number of wavelengths to be observed at the angle \(\alpha\), AC - BD = \(n\lambda\), where \(\lambda\) is the wavelength of the light. Applying some basic trigonometric properties, the following two equations can be shown about the lines:
\[BD = x \cos(\alpha_o) \nonumber \]
and
\[AC = x \cos (\alpha) \nonumber \]
where \(x\) is the distance between the points where the diffraction repeats. Combining the two equations,
Rotating Crystal Method
To describe the periodic, three dimensional nature of crystals, the Laue equations are employed:
\[ a(\cos \alpha – \cos \alpha_o) = nh\lambda \label{eq1} \]
\[b(\cos \beta – \cos \beta_o) = nk\lambda \label{eq2} \]
\[c(\cos \gamma – \cos \gamma_o) = nl\lambda \label{eq3} \]
where \(a\), \(b\), and \(c\) are the three axes of the unit cell, \(\alpha_o\), \(\beta_o\), \(\gamma_o\) are the angles of incident radiation, and \(\alpha\), \(\beta\), and \(\gamma\) are the angles of the diffracted radiation. The \(n\) term refers to the order of the reflections. If \(n\) = 1, then the reflections are first-order reflections. If \(n\) = 2, then the reflections are second-order reflections.
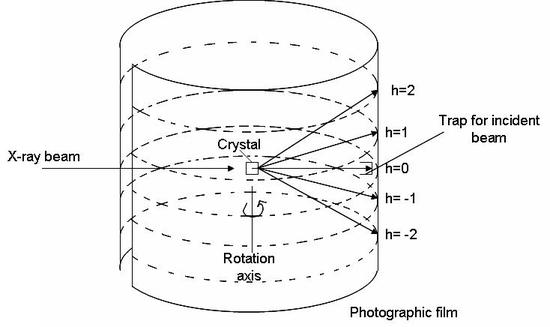
A diffraction signal (constructive interference) will arise when \(h\), \(k\), and \(l\) are integer values. The rotating crystal method employs these equations. X-ray radiation is shown onto a crystal, surrounded by a cylindrical film, as it rotates around one of its unit cell axis. The beam strikes the crystal at a 90-degree angle. Using equation 1 above, we see that if \(\alpha_o\) is 90 degrees, then \(\cos \alpha_o = 0\). For the equation to hold true, we can set h=0, given that \(\alpha\)= 90. The above three equations will be satisfied at various points as the crystal rotates. This gives rise to a diffraction pattern (shown in figure \(\PageIndex{2}\) as multiple h values). The cylindrical film is then unwrapped and developed.
The following equation can be used to determine the length of the axis around which the crystal was rotated:
\[ a = \dfrac{nh \lambda}{\cos (\tan^{-1} (y/r))} \nonumber \]
where a is the length of the axis, y is the distance from \(h=0\) to the \(h\) of interest, \(r\) is the radius of the film (or the distance from the center of the crystal to the detector), and \(\lambda\) is the wavelength of the x-ray radiation used.
Modern diffractometers use electronic scintillation detectors or area detectors that act as a sort of electronic "film." With these detectors, the diffraction data can be sent directly to a computer and analyzed much more rapidly than photographic film. Figure \(\PageIndex{3}\) shows a mounted crystal and its x-ray diffraction pattern.Example \(\PageIndex{1}\)
Bottom) This is a diffraction pattern created from the APS Kinase D63N Mutant of the above crystal (UC Davis Structural Biology Lab)
For a detector with a flat surface, the reflections from a primitive cubic crystal would hit the surface in a pattern similar to that shown in figure \(PageIndex{4}\)
Suppose that you wish to measure the length of a unit cell \(a\) of a crystal that has primitive cubic unit cell. A close up of the experimental set up is shown in Figure \(\PageIndex{4}\). The crystal is aligned so that the incoming x-rays are perpendicular to the a-axis.The distance between the center of the crystal and the detector surface is 5.50 cm. The distance between the detected spots scattered by the 000 planes and the 100 planes is 2.50 cm, and it is scattered at an angle of \(\alpha\). The wavelength of light from the copper x-ray source is 154.4 pm. Determine the length of the unit cell along the a-axis.
Solution
The angle \(\alpha\) can be determined by the fact that \(\tan \alpha\) = \(\dfrac{5.50}{2.50}\). Thus \(\tan ^{-1}(2.2)\), gives \(\alpha\) = 65.56. We can then find the length of a from equation 30.3.10
a =\(\dfrac{(1)(154.4 \, pm)}{\cos (65.56)} = 373.2 \, pm \)
Bragg's Law Applied to Crystals
A second way to analyze the x-ray diffraction is to use Bragg's law. Diffraction of an x-ray beam by crystalline solids occurs when the light interacts with the electron cloud surrounding the atoms of the solid. Because of the periodic crystalline structure of a solid, it is possible to describe it as a series of planes with an equal interplanar distance. As an x-ray beam hits the surface of the crystal at an angle \(\theta\), some of the light will be diffracted at that same angle away from the solid (Figure \(\PageIndex{5}\)). The remainder of the light will travel into the crystal and some of that light will interact with the second plane of atoms. Some of the light will be diffracted at an angle \(theta\), and the remainder will travel deeper into the solid. This process will repeat for the many planes in the crystal. The x-ray beams travel different path lengths before hitting the various planes of the crystal, so after diffraction, the beams will interact constructively only if the path length difference is equal to an integer number of wavelengths (just like in the normal diffraction case above). In the figure below, the difference in path lengths of the beam striking the first plane and the beam striking the second plane is equal to BG + GF. So, the two diffracted beams will constructively interfere (be in phase) only if \(BG + GF = n \lambda\). Basic trigonometry will tell us that the two segments are equal to one another with the interplanar distance times the sine of the angle \(\theta\). So we get:
\[ BG = BC = d \sin \theta \label{1} \]
Thus,
\[ 2d \sin \theta = n \lambda \label{2} \]
This equation is known as Bragg's Law, named after W. H. Bragg and his son, W. L. Bragg; who discovered this geometric relationship in 1912. Bragg's Law relates the distance between two planes in a crystal and the angle of reflection to the x-ray wavelength. The x-rays that are diffracted off the crystal have to be in-phase in order to be observed. Only certain angles that satisfy the following condition will register:
\[ \sin \theta = \dfrac{n \lambda}{2d} \label{3} \]
For historical reasons, the resulting diffraction spectrum is represented as intensity vs. \(2θ\).
Cesium metal has a body-centered cubic crystal structure with a unit cell length of 605.0 pm. Use the Bragg equation to determine the first two observed diffraction angles from the 110 planes when the wavelength of the x-rays is 154.4 pm.
Solution
From section 31.2.3, we found that the interplanar distance for cubic cells can be calculated using the equation
\[\dfrac{1}{d^2} = \dfrac{h^2+k^2+l^2}{a^2} \nonumber \]
If we square equation 31.3.10 we get
\[ \sin^2 \theta = \dfrac{n^2 \lambda^2}{4d^2} \nonumber \]
Combining these two equations, we get
\[ \sin^2 \theta = \dfrac{n^2 \lambda^2}{4a^2}(h^2+k^2+l^2) \nonumber \]
The smallest diffraction angle occurs when \(n = 1\)
\[ \sin^2 \theta = \dfrac{(1^2) (154.4 \ , pm)^2}{4(605.0)^2}(1^2+1^2+0^2) = 0.03257 \nonumber \]
Thus, \(\theta\) = 10.40°
The next largest diffraction angle occurs when \(n = 1\)
\[ \sin^2 \theta = \dfrac{(2^2) (154.4 \ , pm)^2}{4(605.0)^2}(1^2+1^2+0^2) = 0.1303 \nonumber \]
Thus, \(\theta\) = 21.16°
In the next section, we will discuss the factors that determine the phase and the amplitude of the multiple scattered x-rays produced during diffraction.
References
- Skoog, D . A.; Holler, F. J.; Stanley R. C.; Principles of Instrumental Analysis; Thomson Brooks/Cole: Belmont CA, 2007.
- Sands, D. E.; Introduction to Crystallography; Dover Publications, Inc.; New York, 1975
- Drenth, Jan. Principles of Protein x-ray Crystallography, 3rd edition. 2007, Springer Science + Business Media, LLC. pg. 14.
- Rhodes, Gale. Crystallography Made Crystal Clear, 3rd edition. 2006, Elsevier Inc. pg. 33, 55 - 57.
- Actual experimentation done of APS Kinase D63N Penicillium Chrysogenum.
Contributors
- Roman Kazantsev (UC Davis) and Michelle Towles (UC Davis)
- Tom Neils - Grand Rapids Community College

