31.1: The Unit Cell is the Fundamental Building Block of a Crystal
- Page ID
- 14573
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
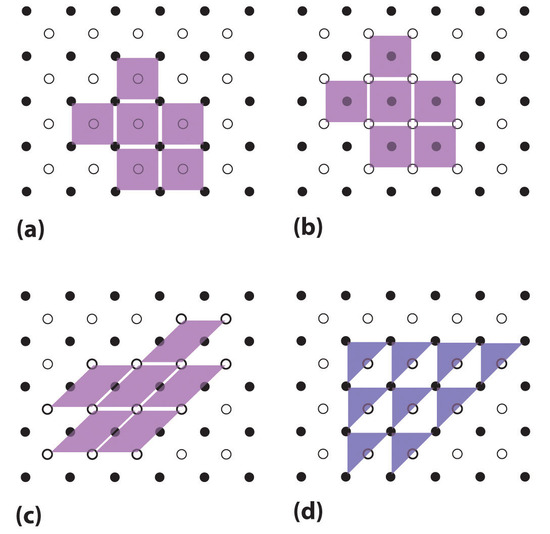
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The regular three-dimensional arrangement of atoms or ions in a crystal is usually described in terms of a space lattice and a unit cell. To see what these two terms mean, let us first consider the two-dimensional patterns shown in Figure \(\PageIndex{1}\). We can think of each of these three structures as a large number of repetitions in two directions. Each light purple parallelogram represents one unit cell. Three valid unit cells and one invalid unit cell for the pattern of light and dark dots are shown.
Finding the unit cell in a three-dimensional crystal structure can be a challenge. Figure \(\PageIndex{2}\) shows three representations of one class of three-dimensional structures: the three types of cubic unit cells. The black lines and gray spheres in the top right corner of the bottom pictures show one unit cell within a larger collection of unit cells.
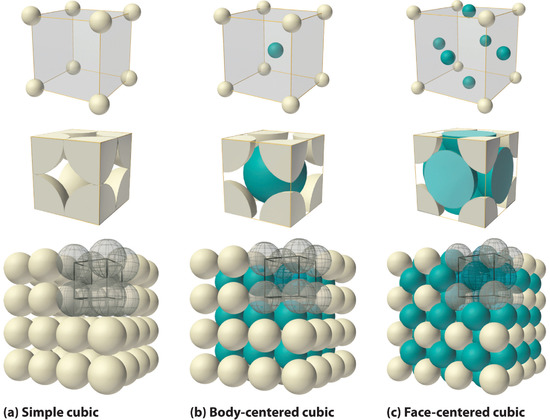
Figure \(\PageIndex{3}\) illustrates the space lattice and the unit cell for a real three-dimensional crystal structure—that of sodium chloride.
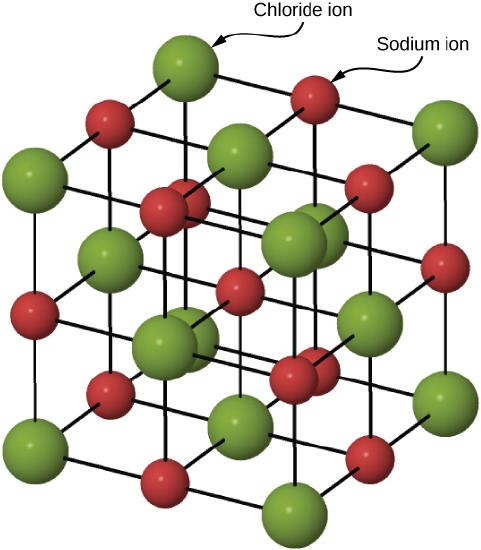

A unit cell for this structure is a cube whose comers are all occupied by sodium ions. Alternatively, the unit cell could be chosen with chloride ions at the corners. The unit cell of sodium chloride contains four sodium ions and four chloride ions. In arriving at such an answer we must bear in mind that many of the ions are shared by several adjacent cells (part c of Figure \(\PageIndex{2}\) shows this well). Specifically, the sodium ions at the centers of the square faces of the cell are shared by two cells, so that only half of each lies within the unit cell. Since there are six faces to a cube, this makes a total of three sodium ions. In the middle of each edge of the unit cell is a chloride ion which is shared by four adjacent cells and so counts one-quarter. Since there are twelve edges, this makes three chloride ions. At each comer of the cube, a sodium ion is shared by eight other cells. Since there are eight comers, this totals to one more sodium ion. Finally, there is a chloride ion in the body of the cube unshared by any other cell. The grand total is thus four sodium and four chloride ions.
A general formula can be derived from the arguments just presented for counting N, the number of atoms or ions in a unit cell. It is
\[N=N_{\text{body}}\text{ + }\frac{N_{\text{face}}}{\text{2}}\text{ + }\frac{N_{\text{edge}}}{\text{4}}\text{ + }\frac{N_{\text{corner}}}{\text{8}}\nonumber \]
Crystal Systems
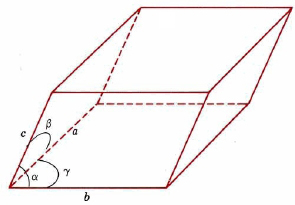
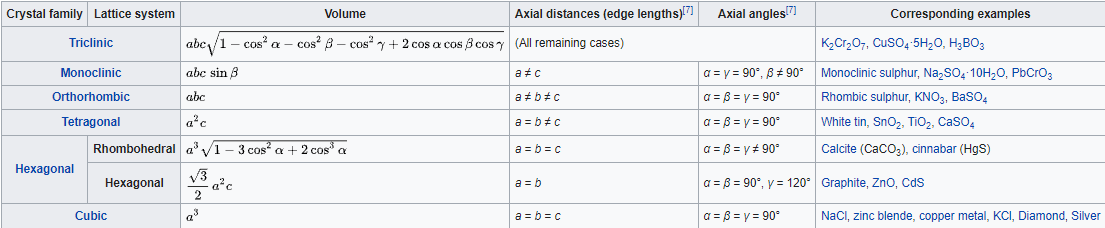
Unit cells need not be cubes, but they must be parallel-sided, three-dimensional figures. A general example is shown in Figure \(\PageIndex{4}\). Such a cell can be described in terms of the lengths of three adjacent edges, a, b, and c, and the angles between them, α, β, and γ.
Crystals are usually classified as belonging to one of fourteen Bravais lattices, depending on the shape of the unit cell and the number of atoms in the unit cell. These fourteen systems are shown in Figure \(\PageIndex{5}\) below. Figure \(\PageIndex{6}\) lists the details about each of the lattice systems.
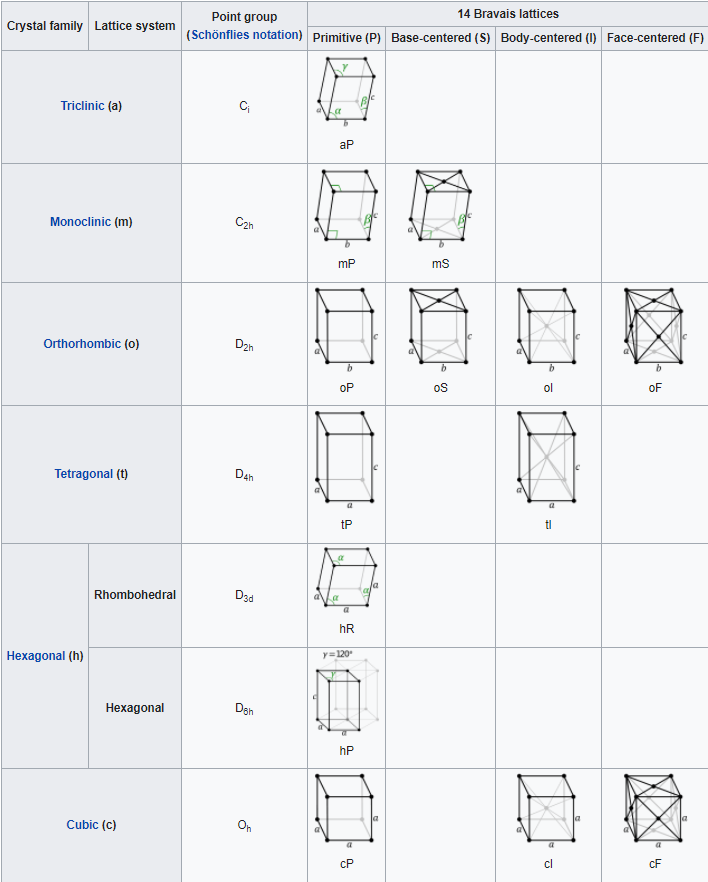
The simplest lattice system is the cubic system, in which all edges of the unit cell are equal and all angles are 90°. The tetragonal and orthorhombic systems also feature rectangular cells, but the edges are not all equal. In the remaining systems, some or all of the angles are not 90°. The least symmetrical is the triclinic, in which no edges are equal and no angles are equal to each other or to 90°.
Close-Packed Systems
An important class of crystal structures is found in many metals and also in the solidified noble gases where the atoms (which are all the same) are packed together as closely as possible. Most of us are familiar with the process of packing spheres together, either from playing with marbles or BB’s as children or from trying to stack oranges or other round fruit into a pyramid. On a level surface we can easily arrange a collection of spheres of the same size into a very compact hexagonal layer in which each sphere is touching six of its fellows, as seen Figure \(\PageIndex{7}\).

Then we can add a second layer so that each added sphere snuggles into a depression between three spheres in the layer below. Within this second layer each sphere also contacts six neighbors, and the layer is identical to the first one. It appears that we can add layer after layer indefinitely, or until we run out of spheres. Each sphere will be touching twelve of its fellows since it is surrounded by six in the same plane and nestles among three in the plane above and three in the plane below. We say that each sphere has a coordination number of 12. It is impossible to make any other structure with a larger coordination number, that is, to pack more spheres within a given volume. Accordingly the structure just described is often referred to as a close-packed structure.
It turns out that there are two ways to create a close-packed structure. These two ways are shown in Figure \(\PageIndex{8}\).
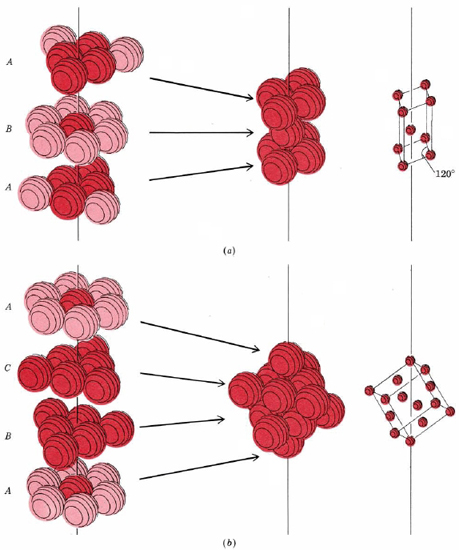
In part a of Figure \(\PageIndex{8}\) the first layer of spheres has been labeled A and the second labeled B to indicate that spheres in the second layer are not directly above those in the first. The third layer is directly above the first, and so it is labeled A. If we continue in the fashion shown, adding alternately A, then B, then A layers, we obtain a structure whose unit cell (shown in part a) has two equal sides with an angle of 120° between them. Other angles are 90°, and so the cell belongs to the hexagonal crystal system. Hence this structure is called hexagonal close packed (hcp).
In part b of Figure \(\PageIndex{8}\) the first layer of spheres has been labeled A and the second labeled B to indicate that spheres in the second layer are not directly above those in the first. In this packing system, the third layer is labeled C because it is not directly above the first or the second layer; it has its own unique orientation. If we continue in the fashion shown, adding alternately A, then B, then C layers, we obtain a structure whose unit cell (shown in part b) that has three equal sides with all angles at 90°, and so the cell belongs to the cubic crystal system. Hence this structure is called cubic close packed (ccp). To repeat, in both the hexagonal close-packed and the cubic close-packed structures each sphere has 12 nearest neighbors.
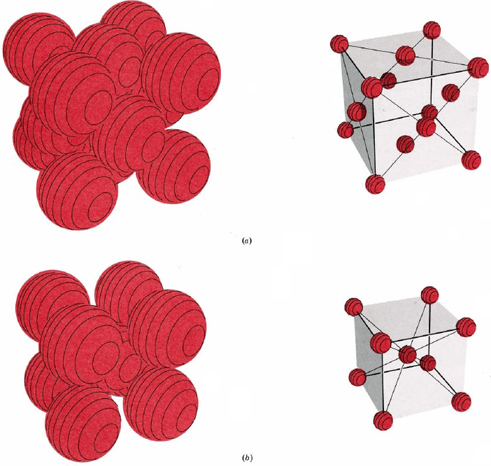
Figure \(\PageIndex{9}\) shows two types of cubic lattices, the face-centered cubic and the body-centered cubic. The unit cell of a body-centered cubic (bcc) crystal is similar to the fcc structure except that, instead of spheres in the faces, there is a single sphere in the center of the cube. This central sphere is surrounded by eight neighbors at the corners of the unit cell, giving a coordination number of 8. Hence the bcc structure is not as compactly packed as the close-packed structures which had a coordination number 12.
Count the number of spheres in the unit cell of (a) a face-centered cubic structure, and (b) a body-centered cubic structure.
Solution
Referring to Figure \(\PageIndex{9}\) and using the equation:
\[N=N_{\text{body}}\text{ + }\frac{N_{\text{face}}}{\text{2}}\text{ + }\frac{N_{\text{edge}}}{\text{4}}\text{ + }\frac{N_{\text{corner}}}{\text{8}} \nonumber \]
we find
b) \[N=\text{1 + 0 + 0 + }\frac{\text{8}}{\text{8}}=\text{2} \nonumber \]
Silicon has the same crystal structure as diamond. Techniques are now available for growing crystals of this element which are virtually flawless. Analysis of some of these perfect crystals found the side of the unit cell to be 543.102064 pm long. The unit cell is a cube containing eight Si atoms, but is only one of the simple cubic cells discussed already. From the isotope make up, molar mass and density of the crystals, it was determined that one mole of Si in this crystal form has a volume of 12.0588349×10-6 m3. Determine NA from this data.
Solution This problem uses knowledge of silicon crystal structure to determine NA. From the edge length, we can obtain the volume of the cubic unit cell. We know that the unit contains eight atoms, and since we know the volume of one mole, we can calculate NA, with the Avogadro constant defined as the number of particles per unit amount of substance.
\[N_{A}= \frac{N*V_{\text{m}}}{V_{\text{unit cell}}}=\frac{8\times{12.0588349}\times{10}^{-6}\text{m}^{3}}{({ 543.102064}\times{10}^{-12}\text{m})^{3}}={6.02214179}\times{10}^{23} \nonumber \]
The values used to determine this value were taken from crystals using X Ray Crystal Density(XRCD), to determine side length. These values were used in the most recent analysis published by the Committee on Data for Science and Technology(CODATA)[1], which standardizes definitions of important scientific constants and units. The value you just calculated is therefore the most accurate determination of Avogadro's constant as of 2007.
It is important to note that the spheres in these models can represent atoms, monatomic ions, polyatomic ions, molecules, or a collection of molecules.
- ↑ Mohr, P.J., Taylor, B.N., and D. B. Newell. "CODATA Recommended Values of the Fundamental Physical Constants:fckLR2006." National Institute of Standards and Technology. December 28, 2007. http://physics.nist.gov/cuu/Constants/codata.pdf
Copper has a density of 8.930 \(\dfrac{grams}{cm^3}\) at 20°C. The molar mass of copper is 63.55 \(\dfrac{grams}{mole}\). Copper crystallizes as a face-centered cubic lattice. Calculate the crystallographic radius of a copper atom.
Solution
By looking at figure \(\PageIndex{2}\) c, you can determine that there are 4 atoms per unit cell. Thus, the mass of a unit cell is
\[\dfrac{(63.55 \, grams/mole)(4 \, atoms/cell)}{6.022 x 10^{23} \, atoms/mole} = 4.221 x 10^{-22} \, grams/cell \nonumber \]
The volume of the unit cell is
\[V_{cell} = \dfrac{4.221 x 10^{-22} \, grams/cell}{8.930 \, grams/cm^3} = 4.727 x 10^{-23} \, cm^3\nonumber \]
The unit cell is cubic, therefore all sides are the same length, and \(V_{cell} = a^3\)
\[a = V_{cell}^{1/3} = 3.616 x 10^{-8} cm = 361.6 \, pm\nonumber \]
As shown in figure \(\PageIndex{2}\) c, the diagonal across the face of the unit cell has a length of 4 times the radius of a copper atom. Thus, the lengtyh of the face diagonal is \(\sqrt{2}a\), which equals \(\sqrt{2}(361.6 \, \text{pm})\) = 511.4 pm. One fourth of 511.4 pm is 127.8 pm.
Contributors and Attributions
Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.
- Tom Neils (Grand Rapids Community College)

