28.7: Rate Constants Are Usually Strongly Temperature Dependent
- Page ID
- 14549
In general, increases in temperature increase the rates of chemical reactions. It is easy to see why, since most chemical reactions depend on molecular collisions. And as we discussed in Chapter 2, the frequency with which molecules collide increases with increased temperature. But also, the kinetic energy of the molecules increases, which should increase the probability that a collision event will lead to a reaction. An empirical model was proposed by Arrhenius to account for this phenomenon. The Arrhenius model (Arrhenius, 1889) can be expressed as
\[ k = A e^{-E_a/RT} \nonumber \]
Although the model is empirical, some of the parameters can be interpreted in terms of the energy profile of the reaction. \(E_a\), for example, is the activation energy, which represents the energy barrier that must be overcome in a collision to lead to a reaction.
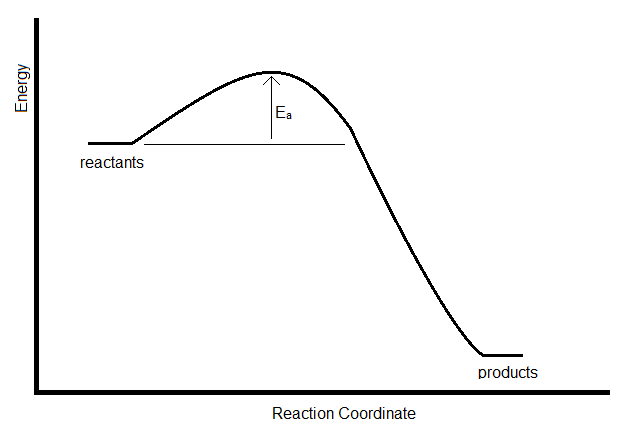
If the rate constant for a reaction is measure at two temperatures, the activation energy can be determined by taking the ratio. This leads to the following expression for the Arrhenius model:
\[ \ln \left( \dfrac{k_1}{k_2} \right) = - \dfrac{E_a}{R} \left( \dfrac{1}{T_2} - \dfrac{1}{T_1} \right) \label{Arrhenius} \]
For a given reaction, the rate constant doubles when the temperature is increased form 25 °C to 35 °C. What is the Arrhenius activation energy for this reaction?
Solution
The energy of activation can be calculated from the Arrhenius Equation (Equation \ref{Arrhenius}).
\[ \ln \left( \dfrac{2k_1}{k_1} \right) = - \dfrac{E_a}{8.314 \, \dfrac{J}{mol\, K}} \left( \dfrac{1}{308\,K} - \dfrac{1}{298\,K} \right) \nonumber \]
From this reaction:
\[E_a = 52.9\, kJ/mol \nonumber \]
Preferably, however, the rate constant is measured at several temperatures, and then the activation energy can be determined using all of the measurements, by fitting them to the expression
\[ \ln (k) = - \dfrac{E_a}{RT} + \ln (A) \nonumber \]
This can be done graphically by plotting the natural logarithm of the rate constant as a function of \(1/T\) (with the temperature measured in K). The result should be a straight line (for a well-behaved reaction!) with a slope of \(–E_a/R\).
There are some theoretical models (such as collision theory and transition state theory) which suggest the form of the Arrhenius model, but the model itself is purely empirical. A general feature, however, of the theoretical approaches is to interpret the activation energy as an energy barrier which a reaction must overcome in order to lead to a chemical reaction.

