24.1: A Mixture is a Combination of Two or More Substances
- Page ID
- 14503
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)So far, we have only discussed systems that are comprised of one component. Because a lot of chemistry occurs in mixtures or produces a mixture, chemists need to consider the thermodynamics of mixtures. A mixture can consist of many different components, however, for the sake of simplicity, we will restrict ourselves for now to two-component mixtures. Two-component mixtures can consist of two gases, two liquids, two solids, or even a liquid and a gas.
Partial Quantities and Scaling
Let's consider a two-component system where the volume and number of moles are changing. For example, we could have a system of a certain size of 1 and reduce its size stepwise in successive steps by taking half of it and throwing the other half away. The number of moles of each component, \(n_1\) and \(n_2\), will change as the volume of the system, \(V\), changes:
\[dn_1=n_1dV \nonumber \]
\[dn_2=n_2dV \nonumber \]
The extensive Gibbs free energy will be affected the same way:
\[dG = GdV \nonumber \]
At constant \(T\) and \(P\) we can write:
\[dG = \cancel{-SdT} + \cancel{VdP} + \mu_1dn_1+\mu _2dn_2 \nonumber \]
So:
\[dG = \mu _1dn_1+\mu _2dn_2 \nonumber \]
\[GdV = \mu _1n_1dV+\mu _2n_2dV \nonumber \]
If we integrate this from the original size, 1, down to 0 (or 0 to 1, it does not matter). We get:
\[ \int_0^1 GdV= \int_0^1 \mu _1n_1dV+ \int_0^1 \mu _2n_2dV \nonumber \]
\[G \int_0^1 dV= \mu _1n_1 \int_0^1 dV+\mu _2n_2 \int_0^1 dV \nonumber \]
\[G=\mu _1n_1+\mu _2n_2 \nonumber \]
By the same argument we have:
\[V=\bar{V}_{1}n_1+\bar{V}_{2}n_2 \nonumber \]
where \(\bar{V}_i\) is the partial molar volume for component \(i\). These partial molar volumes are generally a function of composition (and \(P\), \(T\)) and have been tabulated for a number of liquid systems. They allow us to calculate the real volume of a binary mixture. Volumes are generally speaking not strictly additive. This fact is typically ignored in volumetric analysis and the use of molarities. Fortunately the deviations are often negligible in dilute solutions.
For phase diagrams, molarity (moles per liter) is not a very suitable quantity to use for concentration due to its volume dependence. Usually we work with mole fractions or molalities (moles per kilogram), where there are no volume dependencies.
Gaseous Mixtures
Gases can always mix in any ratio and mixtures typically act close to ideal unless heavily compressed or brought to low temperatures. The only exception is if the gases react (e.g, HCl and NH3). Gas molecules experience little interaction with each other and, therefore, it does not matter much whether the molecules are different or the same. The total pressure can be computed by adding the partial pressures of the two components (Dalton's Law of Partial Pressures):
\[P_{total} = P_1 + P_2 \label{PreDalton} \]
Liquid Mixtures
There are binary liquid systems that are fully miscible and are said to act as ideal solutions. Liquid molecules typically experience strong interactions with their neighbors. For the solution to be ideal, the interactions must remain equally strong even when the neighboring substance is different. This means they must be chemically similar. For this reason, liquid binaries are often not ideal. The next nearest thing are regular solutions. Even these systems can display phase segregation and limited mutual solubilities at low temperatures. Many liquid-liquid binaries diverge from ideality even more than the regular solutions and many of them are hardly miscible at all.
| Solution/mixture | Interactions | Miscibility |
|---|---|---|
| Ideal gas | none | complete |
| Ideal liquid | strong but similar | complete |
| Regular liquid | strong, modestly dissimilar | not always complete |
| Real liquid | often strongly dissimilar | partial or none |
Solid Mixtures
Solid binaries tend to be even less miscible than liquid binaries to the point that immiscibility is the rule and miscibility is the exception. Even totally miscible systems like electrum (the alloys of silver and gold) are far from ideal.

Another point of practical (kinetic rather than thermodynamic) importance is that even if two compounds are able to form a homogeneous solid solution, it usually takes heating for prolonged periods to get them to mix because solid diffusion is typically very slow. Nevertheless, solid solubility is an important issue for many systems, particularly for metal alloys. Two molecular solid substances that differ vastly in shape, size, polarity and or hydrogen bonding (e.g. organic compounds) typically have negligible mutual solid solubility. The latter fact is frequently exploited in organic chemistry to purify compounds through recrystallization.
Solid solutions are relatively infrequent and never ideal.
Ideal liquid/Ideal Gas Phase Diagrams
Let's mix two liquids together. Liquids typically have different boiling points, with one being more volatile than the other. The vapor pressure of a component scales simply with the equilibrium vapor pressure of the pure component. In the gas phase, Dalton's law is applicable:
\[y_i= \dfrac{P_i}{P_{total}} \label{Dalton} \]
This is a consequence of the fact that ideal gases do not interact. The latter implies that the total pressure is simply the sum of the partial ones:
\[P_{total} = \sum_i^N P_i \nonumber \]
If the liquid solution is ideal, then the vapor pressure of both components follow Raoult's law, which states that the equilibrium vapor pressure above the mixture is the equilibrium pressure of the pure component times the mole fraction:
\[P_i = x_iP^*_i \label{Raoult} \]
- \(P_i\) is the vapor pressure of component \(i\) in the mixture
- \(P^*_i\) is equilibrium vapor pressure of the pure component \(i\).
- \(x_i\) is the mole fraction of \(i^{th}\) component in the liquid phase.
Note that values for pure components are typically indicated by adding an asterisk * superscript.
The idea behind Raoult's law is that if the interactions are similar, it is a matter of random chance which component sits at the interface at any given moment. The equilibrium vapor pressure has to do with the probability that a molecule escapes from the interface into the gas phase and is dependent on both the substances volatility and the number that cover the surface. This leads to Raoult's Law, where we must multiply the vapor pressure of the pure liquid (volatility) by the mole fraction (number on the surface).
Raoult's law seldom holds completely, which is more applicable if the two components are almost chemically identical like two isomers, e.g., 1-propanol and 2-propanol.
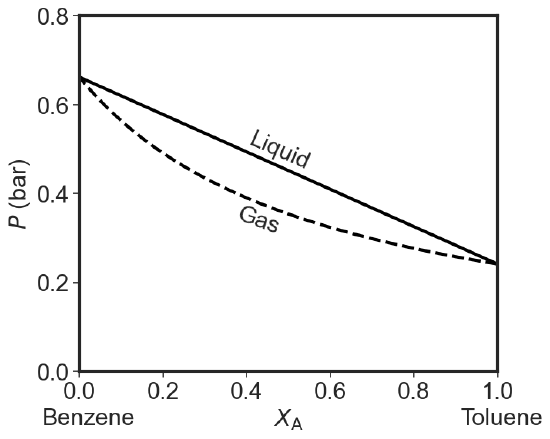
The Pressure Phase Diagram
If we assume that temperature is constant, we can plot the total pressure for both Dalton and Raoult's laws versus composition (of gas: \(y_1\) and liquid: \(x_1\) on the same axis).
Liquid Phase:
\[P_{total} = P_1 + P_2 = x_1P^*_1 +x_2P^*_2 = x_1P^*_1 +(1-x_1)P^*_2= P^*_2- x_1(P^*_2-P^*_1) \label{liquidus} \]
Clearly this is a straight line going from \(P^*_2\) at \(x=0\) to \(P^*_1\) at \(x=1\).
However the composition of the vapor in equilibrium with a liquid at a given mole fraction \(x\) is different than that of the liquid. So \(y\) is not \(x\). If we take Dalton's law (Equation \(\ref{Dalton}\)) and substitute Raoult's Law (Equation \(\ref{Raoult}\)) in the numerator and the straight line in the denominator we get:
\[y_1 = \dfrac{x_1P^*_1}{P^*_2- x_1(P^*_2-P^*_1)} \label{vaporus1} \]
Suppose \(P^*_1 = 50\) Torr and \(P^*_2 = 25\) Torr. If (X_1= 0.6\) what is the composition of the vapor?
We can rearrange Equations \(\ref{liquidus}\) and \(\ref{vaporus1}\) to plot the total pressure as function of \(y_1\):
\[P_{total}= \dfrac{P^*_1P^*_2 }{P^*_1 + (P^*_2-P^*_1)y_1} \label{vaporus2} \]
This is not a straight line.
As you can see when we plot both lines we get a diagram with three regions. At high pressures we just have a liquid. At low pressures we just have a gas. In between we have a phase gap or two phase region. Points inside this region represent states that the system cannot achieve homogeneously. The horizontal tie-line shows which two phases coexists. I used the same 25 and 50 Torr values for the pure equilibrium pressures as in the question above. If you try to make a system with overall composition x and impose a pressure that falls in the forbidden zone you get two phases: a gaseous one that is richer in the more volatile component and a liquid one that is poorer in the volatile component than the overall composition would indicate.
The Temperature Phase Diagram
Note that the question: what phase do we have when? is really a function of both \(P\) and \(T\), so that if we want to represent all our knowledge in a diagram we should make it a three dimensional picture. This is not so easy to draw and not easy to comprehend visually either. This is why we usually look at a 2D cross section of the 3D space.
The above diagram is isothermal: we vary \(P\), keeping \(T\) constant. It is, however, more usual (and easier) to do it the other way around. We keep pressure constant (say 1 bar, that's easy) and start heating things up isobarically.
The boiling points of our mixtures can also be plotted against \(x\) (the liquid composition) and \(y\) (the gaseous one) on the same horizontal axis. Again because in general \(y\) is not equal \(x\) we get two different curves. Neither of them are straight lines in this case and we end up with a lens-shaped two phase region:

What happens to a mixture with a given overall composition x(=x1) when it is brought to a temperature where it boils can be seen at the intersection of a vertical line (an isopleth) at \(x_{overall}\) and a horizontal one (an isotherm) at \(T_{boil}\). If the intersection points in inside the two phase region a vapor phase and a liquid phase result that have a different composition from the overall one. The vapor phase is always richer in the more volatile component (the one with the lowest boiling point, on the left in the diagram). The liquid phase is enriched in the less volatile one.
The Lever Rule
How much of each phase is present is represented by the arrows in the diagram. The amount of liquid is proportional to the left arrow, the amount of gas to the right one (i.e. it works crosswise). The composition of the liquid in equilibrium with the vapor is:
\[x_2 = \dfrac{n^{liq}_2}{n^{liq}_{1+2}} \nonumber \]
\[x_2^*n^{liq}_{1+2} = n^{liq}_2 \nonumber \]
The composition of the vapor is:
\[y_2 = \dfrac{n^{gas}_2}{n^{gas}_{1+2}} \nonumber \]
\[y_2^*n^{gas}_{1+2} = n^{gas}_2 \nonumber \]
The overall composition is:
\[x_{all} = \dfrac{n^{liq+gas}_2 }{n^{liq+gas}_{1+2}} \nonumber \]
\[x_{all}^*n^{liq+gas}_{1+2} = n^{gas}_2+n^{liq}_2 \nonumber \]
\[x_{all}^*n^{liq+gas}_{1+2} = y_2^*n^{gas}_{1+2}+x_2^*n^{liq}_{1+2} \nonumber \]
\[x_{all}^*n^{gas}_{1+2}+x_{all}^*n^{liq}_{1+2} = y_2^*n^{gas}_{1+2}+x_2^*n^{liq}_{1+2} \nonumber \]
Thus:
\[ \dfrac{n^{liq}_{1+2} }{n^{gas}_{1+2}} = \dfrac{y_2-x_{all}}{ x_{all}-x_2} \nonumber \]
Distillation
The difference in composition between the gas and the liquid can be exploited to separate the two components, at least partially. We could trap the vapor and cool it down to form a liquid with a different composition. We could then boil it again and repeat the process. Each time the vapor will be more enriched in the volatile phase whereas the residual liquid is more enriched in the less volatile one. This process is known as distillation. In practice the process is done one a fractionation column which makes it possible to have a series of vapor-liquid equilibria at once.
A good degree of purity can be reached this way, although 100% purity would take an infinite number of distillation steps.