20.4: The Second Law of Thermodynamics
- Page ID
- 13718
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Spontaneity of an isolated system
An isolated system is a little more than just adiabatic. In the latter heat cannot get in or out. In an isolated system nothing gets in or out, neither heat nor mass nor even any radiation, such as light. The isolated system is like a little universe all to itself.
Let us consider a zero law process. We have two identical blocks of metal, say aluminum. They are each at thermal equilibrium, but at different temperatures. They are brought into contact with each other but isolated from the rest of the universe.
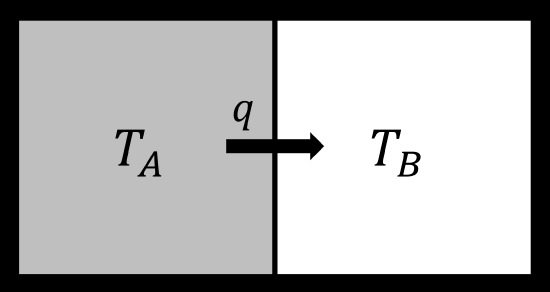
- Zeroth law: Heat will flow from hot to cold
- First law: There is no change in total energy
so:
\[dU_A= -dU_B \nonumber \]
There is also no work so:
\[dU_A = \delta q_A + 0 \nonumber \]
Because U is a state function this makes \(q\) a state function as well, otherwise this equality does not hold. As there is only one term on the right there is only one path (along q). So we could write:
\[dU_A = dq_A \nonumber \]
This implies that we do not need to worry about reversible and irreversible paths as there is only one path. Since:
\[dS = \dfrac{\delta q_{rev}}{T} \nonumber \]
In this particular case:
\[TdS = \delta q_{rev} = dU \nonumber \]
Thus we get:
\[ dS = \dfrac{dU_A}{T_A} + \dfrac{dU_B}{T_B} = \dfrac{dU_A}{T_A} - \dfrac{dU_A}{T_B} = dU_A \left( \dfrac{1}{T_A} - \dfrac{1}{T_B} \right) \nonumber \]
Clearly as long as the two temperatures are not the same \(dS\) is not zero and entropy is not conserved. Instead it is increasing. Over time, the temperatures will become the same (if the blocks are identical, the final temperature is the average of \(T_A\) and \(T_B\)) and the entropy will reach a maximum.

For our two identical blocks of metal (with same heat capacity, \(C_V\)), we can, in fact, derive that the entropy change:
\[\Delta S = C_V \ln \left[\dfrac{T_A^2 + T_B^2}{4T_AT_B}\right]. \nonumber \]
This is indeed a positive quantity. In general, we can say for an isolated system:
\[dS \ge 0 \nonumber \]
Thus if we are dealing with a spontaneous (and isolated) process \(dS >0\) and entropy is being produced. This gives us a criterion for spontaneity.
Entropy exchange of an open system
In an isolated system \(dS\) represents the produced entropy \(dS_{prod}\) and this is a good criterion for spontaneity. Of course the requirement that the system is isolated is very restrictive and makes the criterion as good as useless... What happens in a system that can exchange heat with the rest of the universe? We do have entropy changes in that case, but part of them may have nothing to do with production, because we also have to consider the heat that is exchanged.
\[dS = dS_{prod} + dS_{exchange} \nonumber \]
If the process is reversible (that is completely non-spontaneous) we are dealing with \(\delta q_{rev}\) so that \(dS_{exchange} = \delta q_{rev} /T\), but that is also what \(dS_{tot}\) is equal to (by definition). This leaves no room for entropy production.
So we have:
Isolated: \(dS = dS_{prod} + 0\)
Reversible \(dS = 0 + \delta q_{rev}/T\)
Notice that this demonstrates that for non-isolated systems entropy change is not a good criterion for spontaneity at all... In the case the heat exchange is irreversible part of the entropy is entropy production by the system:
Irreversible: \(dS = dS_{prod} + \delta q_{irrev}/T\)
\(dS > \delta q_{irrev}/T\) in this case.
Generalizing the isolated, irreversible and reversible cases we may say:
\[dS \ge \dfrac{δq}{T} \nonumber \]
This is the Clausius inequality.

