19.12: Heats of Reactions Can Be Calculated from Tabulated Heats of Formation
- Page ID
- 13710
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Reaction enthalpies are important, but difficult to tabulate. However, because enthalpy is a state function, it is possible to use Hess’ Law to simplify the tabulation of reaction enthalpies. Hess’ Law is based on the addition of reactions. By knowing the reaction enthalpy for constituent reactions, the enthalpy of a reaction that can be expressed as the sum of the constituent reactions can be calculated. The key lies in the canceling of reactants and products that °Ccur in the “data” reactions but not in the “target reaction.
Find \(\Delta H_{rxn}\) for the reaction
\[2 CO(g) + O_2(g) \rightarrow 2 CO_2(g) \nonumber \]
Given
\[C(gr) + ½ O_2(g) \rightarrow CO(g) \nonumber \]
with \(\Delta H_1 = -110.53 \,kJ\)
\[C(gr) + O_2(g) \rightarrow CO_2(g) \nonumber \]
with \(\Delta H_2 = -393.51\, kJ\)
Solution
The target reaction can be generated from the data reactions.
\[ {\color{red} 2 \times} \left[ CO(g) \rightarrow C(gr) + O_2(g) \right] \nonumber \]
plus
\[ { \color{red} 2 \times} \left[ C(gr) + 2 O_2(g) \rightarrow 2 CO_2(g) \right] \nonumber \]
equals
\[2 CO(g) + O_2(g) \rightarrow 2 CO_2(g) \nonumber \]
so
\[{ \color{red} 2 \times} \Delta H_1 = -787.02 \, kJ \nonumber \]
\[{ \color{red} 2 \times} \Delta H_2 = 221.06\, kJ \nonumber \]
\[ { \color{red} 2 \times} \Delta H_1 + { \color{red} 2 \times} \Delta H_2 = -565.96 \,kJ \nonumber \]
Standard Enthalpy of Formation
One of the difficulties with many thermodynamic state variables (such as enthalpy) is that while it is possible to measure changes, it is impossible to measure an absolute value of the variable itself. In these cases, it is necessary to define a zero to the scale defining the variable. For enthalpy, the definition of a zero is that the standard enthalpy of formation of a pure element in its standard state is zero. All other enthalpy changes are defined relative to this standard. Thus it is essential to very carefully define a standard state.
The standard state of a substance is the most stable form of that substance at 1 atmosphere pressure and the specified temperature.
Using this definition, a convenient reaction for which enthalpies can be measured and tabulated is the standard formation reaction. This is a reaction which forms one mole of the substance of interest in its standard state from elements in their standard states. The enthalpy of a standard formation reaction is the standard enthalpy of formation (\(\Delta H_{f^o}\)). Some examples are
- \(NaCl(s)\): \[Na(s) + ½ Cl_2(g) \rightarrow NaCl(s) \nonumber \] with \(\Delta H_f^o = -411.2\, kJ/mol\)
- \(C_3H_8(g)\): \[3 C(gr) + 4 H_2(g) \rightarrow C_3H_8(g) \nonumber \] with \(\Delta H_f^o = -103.8\, kJ/mol\)
It is important to note that the standard state of a substance is temperature dependent. For example, the standard state of water at -10 °C is solid, whereas the standard state at room temperature is liquid. Once these values are tabulated, calculating reaction enthalpies becomes a snap. Consider the heat combustion (\(\Delta H_c\)) of methane (at 25 °C) as an example.
\[CH_4(g) + 2 O_2(g) \rightarrow CO_2(g) + 2 H_2O(l) \nonumber \]
The reaction can expressed as a sum of a combination of the following standard formation reactions.
\[C(gr) + 2 H_2(g) \rightarrow CH_4(g) \nonumber \]
with \(\Delta H_f^o = -74.6\, kJ/mol\)
\[C(gr) + O_2(g) \rightarrow CO_2(g) \nonumber \]
with \(\Delta H_f^o = -393.5\, kJ/mol\)
\[H_2(g) + ½ O_2(g) \rightarrow H_2O(l) \nonumber \]
with \(\Delta H_f^o = -285.8 \,kJ/mol\)
The target reaction can be generated from the following combination of reactions
\[{ \color{red} -1 \times} \left[ C(gr) + 2 H_2(g) \rightarrow CH_4(g)\right] \nonumber \]
\[CH_4(g) \rightarrow C(gr) + 2 H_2(g) \nonumber \]
with \(\Delta H_f^o ={ \color{red} -1 \times} \left[ -74.6\, kJ/mol \right]= 74.6\, kJ/mol\)
\[C(gr) + O_2(g) \rightarrow CO_2(g) \nonumber \]
with \(\Delta H_f^o = -393.5\, kJ/mol\)
\[{ \color{red} 2 \times} \left[ H_2(g) + ½ O_2(g) \rightarrow H_2O(l) \right] \nonumber \]
\[ 2H_2(g) + O_2(g) \rightarrow 2H_2O(l) \nonumber \]
with \(\Delta H_f^o = {\color{red} 2 \times} \left[ -285.8 \,kJ/mol \right] = -571.6\, kJ/mol\).
\[CH_4(g) + 2 O_2(g) \rightarrow CO2_(g) + 2 H_2O(l) \nonumber \]
with \(\Delta H_c^o = -890.5\, kJ/mol\)
Alternately, the reaction enthalpy could be calculated from the following relationship
\[\Delta H_{rxn} = \sum_{products} \nu \cdot \Delta H_f^o - \sum_{reactants} \nu \cdot \Delta H_f^o \nonumber \]
where \(\nu\) is the stoichiometric coefficient of a species in the balanced chemical reaction. For the combustion of methane, this calculation is
\[ \begin{align} \Delta _{rxn} & = (1\,mol) \left(\Delta H_f^o(CO_2)\right) + (2\,mol) \left(\Delta H_f^o(H_2O)\right) - (1\,mol) \left(\Delta H_f^o(CH_4)\right) \\ & = (1\,mol) (-393.5 \, kJ/mol) + (2\,mol) \left(-285.8 \, kJ/mol \right) - (1\,mol) \left(-74.6 \, kJ/mol \right) \\ & = -890.5 \, kJ/mol \end{align} \nonumber \]
A note about units is in order. Note that reaction enthalpies have units of kJ, whereas enthalpies of formation have units of kJ/mol. The reason for the difference is that enthalpies of formation (or for that matter enthalpies of combustion, sublimation, vaporization, fusion, etc.) refer to specific substances and/or specific processes involving those substances. As such, the total enthalpy change is scaled by the amount of substance used. General reactions, on the other hand, have to be interpreted in a very specific way. When examining a reaction like the combustion of methane
\[CH_4(g) + 2 O_2(g) \rightarrow CO_2(g) + 2 H_2O(l) \nonumber \]
with \(\Delta H_{rxn} = -890.5\, kJ\). The correct interpretation is that the reaction of one mole of CH4(g) with two moles of O2(g) to form one mole of CO2(g) and two moles of H2O(l) releases 890.5 kJ at 25 °C.
Ionization Reactions
Ionized species appear throughout chemistry. The energy changes involved in the formation of ions can be measured and tabulated for several substances. In the case of the formation of positive ions, the enthalpy change to remove a single electron at 0 K is defined as the ionization potential.
\[ M(g) \rightarrow M^+(g) + e^- \nonumber \]
with \(\Delta H (0 K) \equiv 1^{st} \text{ ionization potential (IP)}\)
The removal of subsequent electrons requires energies called the 2nd Ionization potential, 3rd ionization potential, and so on.
\[M^+(g) \rightarrow M^{2+}(g) + e^- \nonumber \]
with \(\Delta H(0 K) ≡ 2^{nd} IP\)
\[M^{2+}(g) \rightarrow M^{3+}(g) + e^- \nonumber \]
with \(\Delta H(0 K) ≡ 3^{rd} IP\)
An atom can have as many ionization potentials as it has electrons, although since very highly charged ions are rare, only the first few are important for most atoms.
Similarly, the electron affinity can be defined for the formation of negative ions. In this case, the first electron affinity is defined by
\[X(g) + e^- \rightarrow X^-(g) \nonumber \]
with \(-\Delta H(0 K) \equiv 1^{st} \text{ electron affinity (EA)}\)
The minus sign is included in the definition in order to make electron affinities mostly positive. Some atoms (such as noble gases) will have negative electron affinities since the formation of a negative ion is very unfavorable for these species. Just as in the case of ionization potentials, an atom can have several electron affinities.
\[X^-(g) + e^- \rightarrow X^{2-}(g) \nonumber \]
with \(-\Delta H(0 K) ≡ 2^{nd} EA\).
\[X^{2-}(g) + e^- \rightarrow X^{3-}(g) \nonumber \]
with \(-\Delta H(0 K) ≡ 3^{rd} EA\).
Average Bond Enthalpies
In the absence of standard formation enthalpies, reaction enthalpies can be estimated using average bond enthalpies. This method is not perfect, but it can be used to get ball-park estimates when more detailed data is not available. A bond dissociation energy \(D\) is defined by
\[XY(g) \rightarrow X(g) + Y(g) \nonumber \]
with \(\Delta H \equiv D(X-Y)\)
In this process, one adds energy to the reaction to break bonds, and extracts energy for the bonds that are formed.
\[\Delta H_{rxn} = \sum (\text{bonds broken}) - \sum (\text{bonds formed}) \nonumber \]
As an example, consider the combustion of ethanol:
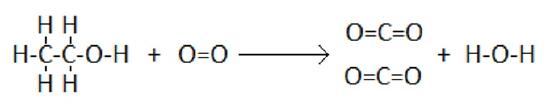
In this reaction, five C-H bonds, one C-C bond, and one C-O bond, and one O=O bond must be broken. Also, four C=O bonds, and one O-H bond are formed.
| Bond | Average Bond Energy (kJ/mol) |
|---|---|
| C-H | 413 |
| C-C | 348 |
| C-O | 358 |
| O=O | 495 |
| C=O | 799 |
| O-H | 463 |
The reaction enthalpy is then given by
\[ \begin{align} \Delta H_c = \, &5(413 \,kJ/mol) + 1(348\, kJ/mol) + 1(358 \,kJ/mol) \nonumber \\ & + 1(495\, kJ/mol) - 4(799 \,kJ/mol) – 2(463\, kJ/mol) \nonumber \\ =\,& -856\, kJ/mol \end{align} \nonumber \]
Because the bond energies are defined for gas-phase reactants and products, this method does not account for the enthalpy change of condensation to form liquids or solids, and so the result may be off systematically due to these differences. Also, since the bond enthalpies are averaged over a large number of molecules containing the particular type of bond, the results may deviate due to the variance in the actual bond enthalpy in the specific molecule under consideration. Typically, reaction enthalpies derived by this method are only reliable to within ± 5-10%.

