18.5: Most Molecules are Rotationally Excited at Ordinary Temperatures
- Page ID
- 13695
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The rotational quantum number is \(J\) and the energy of the rotations is:
\[E(J)= \tilde{B} J(J+1) \nonumber \]
Where \(\tilde{B}\) is in units of cm-1 and is equivalent to:
\[\frac{h}{8\pi^2Ic} \nonumber \]
Where \(c\) is the speed of light in units of cm-1. However, with the exception of the ground state (i.e., \(J=0\)), multiple eigenstates exist for a given value of \(J\). This is a form of degeneracy, (\(g\)), and the number of levels per energy goes as 1, 3, 5, 7, 9 etc or:
\[g(J)=2J+1 \nonumber \]
Therefore, the summation to find the partition function \(q_\text{rot}(T)\) contains an extra factor \(g=2J+1\). This factor is mathematically very handy, because it is the derivative of:
\[g(J)=J(J+1) \nonumber \]
This makes it possible to change variables to \(X=J(J+1)\) and the integration becomes very easy. Notice that just like in the translation partition function, we approximate the summation with an integral. However, because we are dealing with far fewer levels, this is less justified in the rotational case. How justified it is depends on the gas and the temperature we consider. Roughly speaking we should be at a temperature \(T>> Θ_\text{rot}\).
Look at table 18.2. When do we need to actually work out the (discrete) summation instead of making a (continuous) integration out of it?
- Answer
-
Only for the lightest gases like \(\ce{He}\) and \(\ce{H2}\) do we need to worry and then only at pretty low cryogenic circumstances. At room temperature, we can take the rotational levels as a continuous set and use an integral. Notice that the vibrational \(Θ\) values are much larger! At \(T=300\,\text{K}\), usually only a single level is occupied and we are in the discrete limit. On the surface of the sun that would be a different matter of course.
The rotational constant \(B\) is directly linked to the moment of inertia:
\[ I = μr^2\]
Where \(μ\) is the reduced mass of the molecule:
\[\dfrac{1}{μ} = \dfrac{1}{m_1} + \dfrac{1}{m_2} \nonumber \]
and \(r\) is the bond length. Again we can scale the behavior of different systems to one and the same picture by introducing a characteristic temperature:
\[ \Theta_{rot} = \dfrac{hb}{k} = \dfrac{\hbar^2}{2Ik_b} \nonumber \]
As we did for the translations, we can calculate the moment \(\langle \epsilon \rangle\). For vibrations we get a relatively complicated function of temperature. However, for rotations, the moment is simply equal to \(NkT\) and this means that the rotational contribution to the molar \(C_v\) of a diatomic is simply \(R\). As the vibrational and electronic contributions to the heat capacity are typically negligible at room temperature, we get:
- monatomic gas \[C_v= C_v^{trans} = \dfrac{3}{2} nR \nonumber \]
- diatomic \[\begin{align} C_v &= C_v^{trans}+C_v^{rot} \\[4pt] &= \dfrac{3}{2} nR + nR \\[4pt] &= \dfrac{5}{2}nR \end{align} \nonumber \]
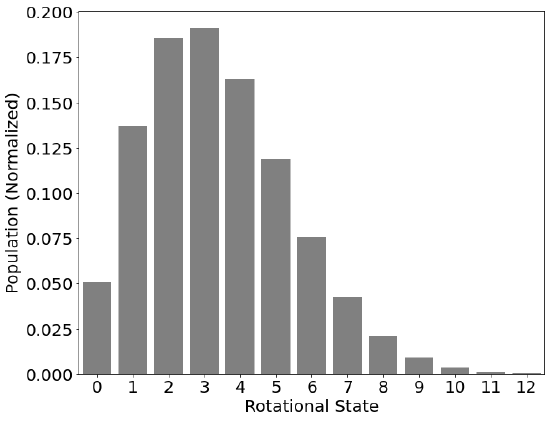
Rotational energies are less than vibrational and electronic energies and, at room temperature, many rotational states will be populated.