13.14: Group Theory Determines Infrared Activity
- Page ID
- 13677
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Determining if a Normal Modes is IR or Raman Active
A transition from \(v \rightarrow v'\) is IR active if the transition moment integral contains the totally symmetric irreducible representation of the point group the molecule belongs to. The transition moment integral is derived from the one-dimensional harmonic oscillator. Using the definition of electric dipole moment \(\mu\), the integral is:
\[ M(v \rightarrow v') = \langle \text{final wavefunction} | \vec{\mu} | \text{initial wavefunction } \rangle \nonumber \]
or in terms of vibrational wavefunctions for a specific normal mode \( | \phi (v) \rangle \)
\[ M(v \rightarrow v') = \langle \phi(v' \neq 0) | \vec{\mu} | \phi (v=0) \rangle \label{M1} \]
assuming the transition from the \(v=0\) wavefunction to the \(v' \neq 0\) wavefunction.
Now, consider the case that \(\vec{μ}\), is a constant and therefore independent of the vibration (i.e., the electric dipole moment does not change during the vibration). This it could be taken outside the integral in Equation \(\ref{M1}\) becomes
\[ M(v \rightarrow v') = \vec{\mu} \langle \phi(v' \neq 0) | \phi (v=0) \rangle \label{M2} \]
Since \(|\phi(v=0) \rangle \) and \(|\phi(v =\neq0) \rangle \) are mutually orthogonal to each other, the integral in Equation \(\ref{M1}\) will equal zero and the transition will not be allowed (i.e., it is forbidden). For the \(M\) to be nonzero, \(\vec{μ}\) must change during a vibration. This selection rule explains why homonuclear diatomic molecules do not produce an IR spectrum. There is no change in dipole moment resulting in a transition moment integral of zero and a transition that is forbidden.
For a transition to be Raman active, the same rules apply. The transition moment integral must contain the totally symmetric irreducible representation of the point group. The integral contains the polarizability tensor \(\alpha\) (usually represented by a square matrix):
\[ M(v \rightarrow v') = \langle \phi(v' \neq 0) | \alpha | \phi (v=0) \rangle \label{M3} \]
Following a similar argument as above, \(\alpha\) must be nonzero for the transition to be allowed and exhibits Raman scattering.
Character Table
For a molecule to be IR active the dipole moment has to change during the vibration. For a molecule to be Raman active the polarizability of the molecule has to change during the vibration. The reducible representation Γvib can also be found by determining the reducible representation of the 3N degrees of freedom of H2O, Γtot. By applying Group Theory it is straightforward to find Γx,y,z as well as UMA (number of unmoved atoms). Again, using water as an example with C2v symmetry where 3N = 9, Γtot can be determined:
| C2v | E | C2 | σ (xz) | σ (yz) | |
|---|---|---|---|---|---|
| Τx,y,z | 3 | -1 | 1 | 1 | |
| UMA | 3 | 1 | 1 | 3 | |
| Γtot | 9 | -1 | 1 | 3 | =3a1 + a2 + 2b1 + 3b2 |
| Note that Γtot contains nine degrees of freedom consistent with 3N = 9. | |||||
Γtot contains Γtranslational, Γrotational as well as Γvibrational. Γtrans can be obtained by finding the irreducible representations corresponding to x,y and z in the right side of the character table, Γrot by finding the ones corresponding to Rx, Ry and Rz. Γvib can be obtained by Γtot - Γtrans - Γrot.
\[Γ_{vib} (H_2O) = (3a_1 + a_2 + 2b_1+ 3b_2) - (a_1 + b_1 + b_2) - (a_2 + b_1 + b_2) = 2a_1 + b_2 \nonumber \]
In order to determine which modes are IR active, a simple check of the irreducible representation that corresponds to x,y and z and a cross check with the reducible representation Γvib is necessary. If they contain the same irreducible representation, the mode is IR active.
For H2O, z transforms as a1, x as b1 and y as b2. The modes a1 and b2 are IR active since Γvib contains 2a1 + b2.
In order to determine which modes are Raman active, the irreducible representation that corresponds to z2, x2-y2, xy, xz and yz is used and again cross checked with Γvib. For H2O, z2 and x2-y2 transform as a1, xy as a2, xz as b1 and yz as b2.The modes a1 and b2 are also Raman active since Γvib contains both these modes.
The IR spectrum of H2O does indeed have three bands as predicted by Group Theory. The two symmetric stretches v1 and v2 occur at 3756 and 3657 cm-1 whereas the bending v3 motion occurs at 1595 cm-1.
In order to determine which normal modes are stretching vibrations and which one are bending vibrations, a stretching analysis can be performed. Then the stretching vibrations can be deducted from the total vibrations in order to obtain the bending vibrations. A double-headed arrow is drawn between the atom as depicted below:
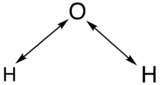
Then a determination of how the arrows transform under each symmetry operation in C2v symmetry will yield the following results:
| C2v | E | C2 | σ (xz) | σ (yz) | |
|---|---|---|---|---|---|
| Γstretch | 2 | 0 | 0 | 2 | = a1 + b2 |
\[Γ_{bend} = Γ_{vib} - Γ_{stretch} = 2a_1 + b_2 -a_1 - b_2 = a_1 \nonumber \]
H2O has two stretching vibrations as well as one bending vibration. This concept can be expanded to complex molecules such as PtCl4-. Four double headed arrows can be drawn between the atoms of the molecule and determine how these transform in D4h symmetry. Once the irreducible representation for Γstretch has been worked out, Γbend can be determined by Γbend = Γvib - Γstretch.
Most molecules are in their zero point energy at room temperature. Therefore, most transitions do originate from the v=0 state. Some molecules do have a significant population of the v=1 state at room temperature and transitions from this thermally excited state are called hot bands.
References
- Merlin, J.C., Cornard, J.P., J. Chem. Educ., 2006, 83 (9), p 1383. DOI: 10.1021/ed083p1393
- McGuinn, C.J., J. Chem. Educ., 1982, 59 (10), p 813. DOI: 10.1021/ed059p813
- Harris, D.C., Bertolucci, M.D., Symmetry and Spectroscopy: An introduction to Vibrational and Electronic Spectroscopy. Dover Publocations, Inc., New York, 1989.
- McQuarrie, D. A., Simon, J.D., Physical Chemistry: A Molecular Approach, University Science Books, Sausalito, California, 1997; 518-521.
- Housecroft, C.E., Sharpe, A.G., Inorganic Chemistry. Pearson Education Limited, England, 2008, 107.
- Atkins, P., dePaula, J., Physical Chemistry, W.H. Freeman and Company, New York, 2002, 520-523.
- Bishop, D.M., Group Theory and Chemistry, Dover Publications, Inc, New York, 1973, 166.

