2.3: Oscillatory Solutions to Differential Equations
- Page ID
- 13377
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Explore the basis of the oscillatory solutions to the wave equation
- Understand the consequences of boundary conditions on the possible solutions
- Rationalize how satisfying boundary conditions forces quantization (i.e., only solutions with specific wavelengths exist)
The boundary conditions for the string held to zero at both ends argue that \(u(x,t)\) collapses to zero at the extremes of the string (Figure 2.3.1 ).
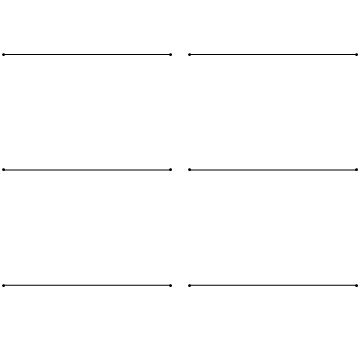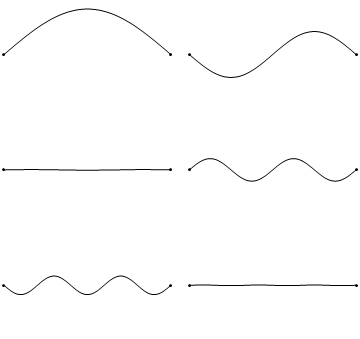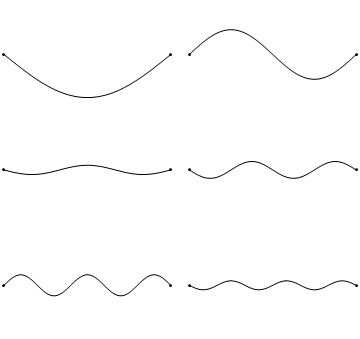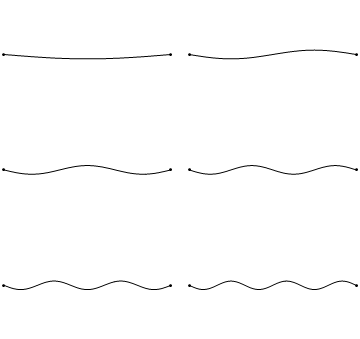
Unfortunately, when \(K>0\), the general solution (Equation 2.2.7) results in a sum of exponential decays and growths that cannot achieve the boundary conditions (except for the trivial solution); hence \(K<0\). This means we must introduce complex numbers due to the \(\sqrt{K}\) terms in Equation 2.2.5. So we can rewrite \(K\):
\[K = - p^2 \label{2.3.1} \]
and Equation 2.2.4b can be
\[\dfrac{d^2X(x)}{dx^2} +p^2 X(x) = 0 \label{2.3.2} \]
The general solution to differential equations of the form of Equation \ref{2.3.2} is
\[X(x) = A e^{ipx} + B e^{-ipx} \label{2.3.3} \]
Verify that Equation \(\ref{2.3.3}\) is the general form for differential equations of the form of Equation \(\ref{2.3.2}\), which when substituted with Equation \(\ref{2.3.1}\) give
\[X(x) = A e^{ipx} + B e^{-ipx} \nonumber \]
Solution
Expand the complex exponentials into trigonometric functions via Euler formula (\(e^{i \theta} = \cos \theta + i\sin \theta\))
\[X(x) = A \left[\cos (px) + i \sin (px) \right] + B \left[ \cos (px) - i \sin (px) \right] \nonumber \]
collecting like terms
\[X(x) = (A + B ) \cos (px) + i (A - B) \sin (px) \label{2.3.6} \]
Introduce new complex constants \(c_1=A+B\) and \(c_2=i(A-B)\) so that the general solution in Equation \(\ref{2.3.6}\) can be expressed as oscillatory functions
\[X(x) = c_1 \cos (px) + c_2 \sin (px) \label{2.3.7} \]
Now let's apply the boundary conditions from Equation 2.2.7 to determine the constants \(c_1\) and \(c_2\). Substituting the first boundary condition (\(X(x=0)=0\)) into the general solutions of Equation \(\ref{2.3.7}\) results in
\[ \begin{align} X(x=0) = c_1 \cos (0) + c_2 \sin (0) &=0 \nonumber \\[4pt] c_1 + 0 &= 0 \nonumber \\[4pt] c_1 &=0 \label{2.3.8c} \end{align} \]
and substituting the second boundary condition (\(X(x=L)=0\)) into the general solutions of Equation \(\ref{2.3.7}\) results in
\[ X(x=L) = c_1 \cos (pL) + c_2 \sin (pL) = 0 \label{2.3.9} \]
we already know that \(c_1=0\) from the first boundary condition so Equation \(\ref{2.3.9}\) simplifies to
\[ c_2 \sin (pL) = 0 \label{2.3.10} \]
Given the properties of sines, Equation \(\ref{2.3.9}\) simplifies to
\[ pL= n\pi \label{2.3.11} \]
with \(n=0\) is the trivial solution that we ignore so \(n = 1, 2, 3...\).
\[ p = \dfrac{n\pi}{L} \label{2.3.12} \]
Substituting Equations \(\ref{2.3.12}\) and \(\ref{2.3.8c}\) into Equation \(\ref{2.3.7}\) results in
\[X(x) = c_2 \sin \left(\dfrac{n\pi x}{L} \right) \nonumber \]
which can simplify to
\[X(x) = c_2 \sin \left( \omega x \right) \nonumber \]
with
\[\omega=\dfrac{n\pi}{L} \nonumber \]
A similar argument applies to the other half of the ansatz (\(T(t)\)).
Given two traveling waves: \[ \psi_1 = \sin{(c_1 x+c_2 t)} \; \textrm{ and } \; \psi_2 = \sin{(c_1 x-c_2 t)} \nonumber \]
- Find the wavelength and the wave velocity of \( \psi_1 \) and \( \psi_2 \)
- Find the following and identify nodes: \[ \psi_+ = \psi_1 + \psi_2 \; \textrm{ and } \; \psi_- = \psi_1 - \psi_2 \nonumber \]
Solution a:
\(\psi_1 \) is a sin function. At every integer \( n \pi \) where \(n=0,\pm 1, \pm 2, ... \), a sin function will be zero. Thus, \( \psi_1 = 0 \) when \(c_1 x + c_2 t = \pi n \). Solving for the x, while ignoring trivial solutions:
\[ x = \frac{n \pi - c_2 t}{c_1} \nonumber \]
The velocity of this wave is:
\[ \frac{dx}{dt} = -\frac{c_2}{c_1} \nonumber \]
Similarly for \( \psi_2 \). At every integer \( n \pi \) where \(n=0,\pm 1, \pm 2, ... \), a sin function will be zero. Thus, \( \psi_2 = 0 \) when \(c_1 x - c_2 t = \pi n \). Solving for x, for \( \psi_2 \):
\[ x = \frac{n \pi + c_2 t}{c_1} \nonumber \]
The velocity of this wave is:
\[ \frac{dx}{dt} = \frac{c_2}{c_1} \nonumber \]
The wavelength for each wave is twice the distance between two successive nodes. In other words,
\[ \lambda = 2(x_{n} - x_{n-1}) = \frac{2 \pi}{c_1} \nonumber \]
Solution b:
Find \( \psi_+ = \psi_1 + \psi_2 \; \textrm{ and } \; \psi_- = \psi_1 - \psi_2 \).
\[ \begin{align*} \psi_+ &= \sin (c_1 x + c_2 t) + \sin (c_1 x - c_2 t) \\[4pt] &= \sin (c_1 x ) \cos (c_2 t) + \cancel{\cos(c_1 x) \sin(c_1 t)} + \sin (c_1 x ) \cos (c_2 t) - \cancel{\cos(c_1 x) \sin(c_1 t)} \\[4pt] &= 2\sin (c_1 x ) \cos (c_2 t) \end{align*} \nonumber \]
This should have a node at every \( x= n \pi / c_1 \) and
\[ \begin{align*} \psi_- &= \sin (c_1 x + c_2 t) - \sin (c_1 x - c_2 t) \\[4pt] &= \cancel{\sin (c_1 x ) \cos (c_2 t)} + \cos(c_1 x) \sin(c_1 t) - \cancel{\sin (c_1 x ) \cos (c_2 t)} + \cos(c_1 x) \sin(c_1 t) \\[4pt] &= 2\cos (c_1 x ) \sin (c_2 t) \end{align*} \nonumber \]

