12.8: The Michaelis-Menten Mechanism
- Page ID
- 84602
The Michaelis-Menten mechanism (Michaelis & Menten, 1913) is one which many enzyme mitigated reactions follow. The basic mechanism involves an enzyme (\(E\), a biological catalyst) and a substrate (\(S\)) which must connect to form an enzyme-substrate complex (\(ES\)) in order for the substrate to be degraded (or augmented) to form a product (\(P\)). The overall reaction is
\[S \rightarrow P \nonumber \]
And the simple two-step mechanism is given by
\[E + S \ce{<=>[k_1][k_{-1}]} ES \label{step1} \]
\[ ES \xrightarrow{k_2} P \label{step2} \]
Notice that the enzyme is necessary for the reaction to proceed, but is not part of the overall stoichiometry (as is the case for any catalyst!).
Equilibrium Approximation Derivation
Applying the equilibrium approximation to the first step
\[ k_1[E][S] \approx k_{-1}[ES] \label{equil} \]
And using a mass conservation relationship on the enzyme (noting that the enzyme must be either in its bare form (\(E\)) or complexed with a substrate (\(ES\))):
\[ [E]_o = [E] + [ES] \nonumber \]
or
\[[E] = [E]_o - [ES] \nonumber \]
Substituting this into the equilibrium expression (Equation \ref{equil}) yields
\[ k_1([E]_o - [ES])[S] = k_{-1}[ES] \nonumber \]
Solving this expression for \([ES]\) stepwise reveals
\[ k_1[E]_o[S] - k_1[ES][S] = k_{-1}[ES] \nonumber \]
\[ k_1[E]_o[S] = k_{-1}[ES] + k_1[ES][S] \nonumber \]
\[= (k_{-1} + k_1 ) [ES] \nonumber \]
\[\dfrac{k_1[E]_o[S]}{k_1[S] + k_{-1}} = [ES] \nonumber \]
Substituting this into the expression for the rate of production of the product \(P\)
\[\dfrac{d[P]}{dt} = k_2[ES] \label{step3} \]
yields
\[\dfrac{d[P]}{dt} = \dfrac{k_2 k_1 [E]_o [S]}{k_1[S] + k_{-1}} \nonumber \]
Multiplying the top and bottom of the expression on the right hand side by 1/k1 gives the result
\[\dfrac{d[P]}{dt} = \dfrac{k_2[E]_o[S]}{[S] + \frac{k_1}{k_{-1}}} \nonumber \]
The ratio of k-1/k1 is the equilibrium constant that describes the dissociation of the enzyme-substrate complex, \(K_d\) in Equation \ref{step1}. Noting that \(k_2[E]_0\) gives the maximum rate (\(V_{max}\)), and that \(\dfrac{d[P]}{dt}\) is the observed reaction rate, the rate law takes the form
\[\text{rate} = \dfrac{V_{max}[S]}{K_d+[S]} \nonumber \]
This is because the maximum reaction rate is achieved when [ES] is low. As [ES] increases, the likelihood of the complex decomposing to reform reactants is higher, slowing the conversion. [ES] will be low if the concentration of the enzyme is much larger than that of the substrate, so there is never a shortage of enzyme available to form the complex with the substrate. However, if the substrate concentration is higher, the lack of available enzyme active sites will slow the reaction and cause it to become 0th order.
In the limit that the substrate concentration is large compared to \(K_d\) (i.e., \(K_d + [S] \approx [S]\)), the reaction ends up zeroth order in substrate.
\[\text{rate} = \dfrac{V_{max}[S]}{K_d+[S]} \approx \dfrac{V_{max}\cancel{[S]}}{\cancel{[S]}} = V_{max} \nonumber \]
Hence, adding more substrate to the system under this limiting condition will have no effect on the observed rate. This is characteristic of a bottleneck in the mechanism, which would happen if there is a shortage of enzyme sites to which the substrate can attach.
In the other extreme, in which \(K_d\) is very large compared to the substrate concentration (i.e., \(K_d + [S] \approx K_d \)), the reaction become first order in substrate.
\[ \text{rate} = \dfrac{V_{max}[S]}{K_d+[S]} \approx \dfrac{V_{max}[S]}{K_d} = \dfrac{V_{max}}{K_d}[S] \nonumber \]
Steady-State Approximation Derivation
In an alternate derivation (Briggs & Haldane, 1925) using the steady state approximation applied to the enzyme-substrate complex
\[\dfrac{[ES]}{dt} = k_1[E][S] - k_{-1}[ES] - k_2[ES] \approx 0 \nonumber \]
Solving for \([ES]\) gives the result
\[ES] = \dfrac{k_1[E][S]}{k_{-1} + k_2} \nonumber \]
or
\[[ES] = \dfrac{[E][S]}{K_m} \nonumber \]
where
\[K_m = \dfrac{k_{-1}+K_2}{k_1} \nonumber \]
\(K_M\) is the Michaelis constant, which is affected by a number of factors, including pH, temperature, and the nature of the substrate itself. Proceeding as before, though the conservation of mass relationship and substitution into the expression for rate (Equation \ref{step3}) results in
\[\dfrac{d[P]}{dt} =\dfrac{V_{max}[S]}{K_m + [S]} \nonumber \]
The advantage to this approach is that it accounts for the loss of \(ES\) complex due to the production of products as well as the decomposition to reform the reactants E and S. As before, in the limit that \([S] \gg K_M\), the reaction reaches its maximum rate (\(V_{max}\)) and becomes independent of any concentrations. However in the limit that \([S] \ll K_M\), the reaction becomes 1st order in \([S]\).

The Michalis constant and Vmax parameters can be extracted in a number of ways. In the Lineweaver-Burk (Lineweaver & Burk, 1934) method, the reciprocal of the rate law is used to create a linear relationship.
\[ \dfrac{1}{\text{rate}} = \dfrac{K_m + [S]}{V_{max}[S]} \nonumber \]
or
\[ \dfrac{1}{\text{rate}} = \dfrac{K_m}{V_{max}} \dfrac{1}{[S]} + \dfrac{1}{V_{max}} \nonumber \]
So a plot of \(1/rate\) as a function of \(1/[S]\) results in a straight line, the slope of which is equal to \(K_M/V_{max}\) and the intercept is \(1/V_{max}\). This is called a Lineweaver–Burk plot.
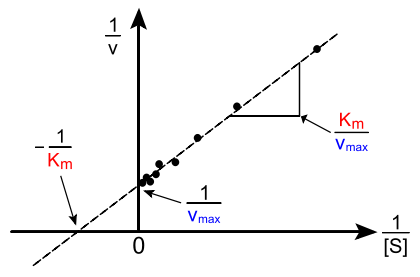
An example of a Lineweaver-Burk plot. (CC BY-SA 3.0; Diberri).


