3.7: Lattice Energy and the Born-Haber Cycle
- Page ID
- 84456
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)An important enthalpy change is the Lattice Energy, which is the energy required to take one mole of a crystalline solid to ions in the gas phase. For \(\ce{NaCl(s)}\), the lattice energy is defined as the enthalpy of the reaction
\[ \ce{ NaCl(s) \rightarrow Na^{+}(g) + Cl^{-}(g) } \nonumber \]
with \(\Delta H\) called the lattice energy (\(\Delta H_{Lat}\)).
The Born-Haber Cycle
A very handy construct in thermodynamics is that of the thermodynamic cycle. This can be represented graphically to help to visualize how all of the pieces of the cycle add together. A very good example of this is the Born-Haber cycle, describing the formation of an ionic solid.
Two pathways can be envisioned for the formation. Added together, the two pathways form a cycle. In one pathway, the ionic solid if formed directly from elements in their standard states.
\[ \ce{Na(s) + 1/2 Cl_2 \rightarrow NaCl(s)} \nonumber \]
with \(\Delta H_f(NaCl)\).
The other pathway involves a series of steps that take the elements from neutral species in their standard states to ions in the gas phase.
\[Na(s) \rightarrow Na(g) \nonumber \]
with \(\Delta H_{sub}(Na)\)
\[Na(g) \rightarrow Na^+(g) + e^- \nonumber \]
with \(1^{st}\, IP(Na)\)
\[½ Cl_2(g) \rightarrow Cl(g) \nonumber \]
with \(½ D(Cl-Cl)\)
\[Cl(g) + e^- \rightarrow Cl^-(g) \nonumber \]
with \(1^{st} EA(Cl)\)
\[Na^+(g) + Cl^-(g) \rightarrow NaCl(s) \nonumber \]
with \(\Delta H_{Lat}(NaCl)\)
It should be clear that when added (after proper manipulation if needed), the second set of reactions yield the first reaction. Because of this, the total enthalpy changes must all add.
\[\Delta H_{sub}(Na) + 1^{st} IP(Na) + ½ D(Cl-Cl) + 1^{st} EA(Cl) + \Delta H_{lat}(NaCl) = \Delta H_f(NaCl) \nonumber \]
This can be depicted graphically, the advantage being that arrows can be used to indicate endothermic or exothermic changes. An example of the Born-Haber Cycle for NaCl is shown below.
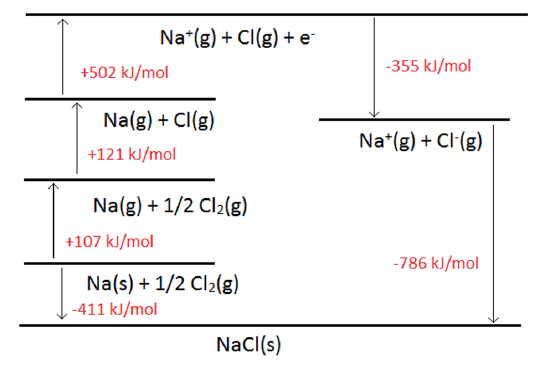
In many applications, all but one leg of the cycle is known, and the job is to determine the magnitude of the missing leg.
Find \(\Delta H_f\) for KBr given the following data.
\[\ce{K(s) \rightarrow K(g)} \nonumber \]
with \(\Delta H_{sub} = 89\, kJ/mol\)
\[\ce{Br_2(l) \rightarrow Br_2(g) } \nonumber \]
with \(\Delta H_{vap} = 31\, kJ/mol\)
\[\ce{Br_2(g) \rightarrow 2 Br(g)} \nonumber \]
with \(D(Br-Br) = 193\, kJ/mol\)
\[\ce{K(g) \rightarrow K^+(g) + e^- } \nonumber \]
with \(1^{st} IP(K) = 419 kJ/mol\)
\[\ce{Br(g) + e^- \rightarrow Br^-(g) } \nonumber \]
with \(1^{st} EA(Br) = 194 kJ/mol\)
\[\ce{K^+(g) + Br^-(g) \rightarrow KBr(s)} \nonumber \]
with \(\Delta H_{Lat} = 672 kJ/mol\)
- Answer
-
\(\Delta H_f = -246 \,kJ/mol\)
Note: This cycle required the extra leg of the vaporization of Br2. Many cycles involve ions with greater than unit charge and may require extra ionization steps as well!


