3.E: First Law of Thermodynamics (Exercises)
- Page ID
- 84457
Q3.1
In the attempt to measure the heat equivalent of mechanical work (as Joule did in his famous experiment) a student uses an apparatus similar to that shown below:
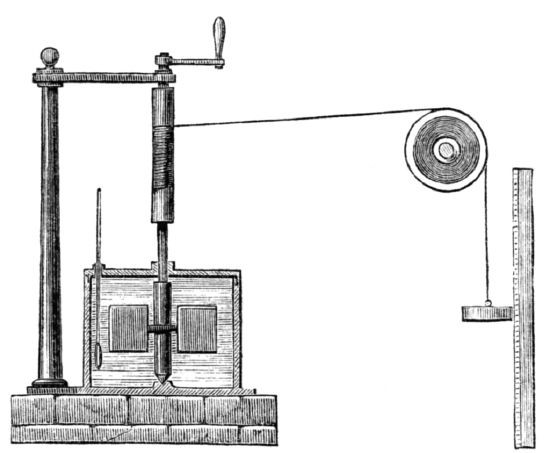
The 1.50 kg weight is lifted 30.0 cm against the force due to gravity (9.8 N). If the specific heat of water is 4.184 J/(g °C), what is the expected temperature increase of the 1.5 kg of water in the canister?
Q3.2
1.00 mol of an ideal gas, initially occupying 12.2 L at 298 K, expands isothermally against a constant external pressure of 1.00 atm until the pressure of the gas is equal to the external pressure. Calculate \(\Delta p\), \(q\), \(w\), \(\Delta U\), and \(\Delta H\) for the expansion.
Q3.3
Consider 1.00 mol of an ideal gas expanding isothermally at 298 K from an initial volume of 12.2 L to a final volume of 22.4 L. Calculate \(\Delta p\), \(q\), \(w\), \(\Delta U\), and \(\Delta H\) for the expansion.
Q3.4
Consider 1.00 mol of an ideal gas (CV = 3/2 R) Occupying 22.4 L that undergoes an isochoric (constant volume) temperature increase from 298 K to 342 K. Calculate \(\Delta p\), \(q\), \(w\), \(\Delta U\), and \(\Delta H\) for the change.
Q3.5
Consider 1.00 mol of an ideal gas (Cp = 5/2 R) initially at 1.00 atm that undergoes an isobaric expansion from 12.2 L to 22.4 L. Calculate \(\Delta T\), \(q\), \(w\), \(\Delta U\), and \(\Delta H\) for the change.
Q3.6
Consider 1.00 mol of an ideal gas (CV = 3/2 R) initially at 12.2 L that undergoes an adiabatic expansion to 22.4 L. Calculate \(\Delta T\), \(q\), \(w\), \(\Delta U\), and \(\Delta H\) for the change.
Q3.7
Derive an expression for the work of an isothermal, reversible expansion of a gas that follows the equation of state (in which \(a\) is a parameter of the gas)
\[ pV = nRT -\dfrac{an^2}{V}\]
from \(V_1\) to \(V_2\).
Q3.8
Use the following data [Huff, Squitieri, and Snyder, J. Am. Chem. Soc., 70, 3380 (1948)] to calculate the standard enthalpy of formation of tungsten carbide, \(WC(s)\).
| Reaction | \(\Delta H^o\) (kJ) |
|---|---|
| \(C(gr) + O_2(g) \rightarrow CO_2(g)\) | -393.51 |
| \(WC(s) + 5/2 O_2(g) \rightarrow WO_3(s) + CO_2(g)\) | -1195.79 |
| \(W(s) + 3/2 O_2(g) \rightarrow WO_3(s)\) | -837.42 |
Q3.9
The standard molar enthalpy of combustion (\(\Delta H_c\)) of propane gas is given by
\[C_3H_8(g) + 5 O_2(g) \rightarrow 3 CO_2(g) + 4 H_2O(l)\]
with \(\Delta H_c = -2220 \,kJ/mol\)
The standard molar enthalpy of vaporization (\(\Delta H_{vap}\)) for liquid propane
\[C_3H_8(l) \rightarrow C_3H_8(g)\]
with \(\Delta H_{vap} = 15\, kJ/mol\)
- Calculate the standard enthalpy of combustion of liquid propane.
- Calculate the standard internal energy change of vaporization (\(\Delta U_{vap}\)) for liquid propane.
- Calculate the standard internal energy change of combustion (\(\Delta H_c\)) for liquid propane.
Q3.10
The enthalpy of combustion (\(\Delta H_c\)) of aluminum borohydride, \(Al(BH_4)_3(l)\), was measured to be -4138.4 kJ/mol [Rulon and Mason, J. Am. Chem. Soc., 73, 5491 (1951)]. The combustion reaction for this compound is given by
\[ Al(BH_4)_3(l) + 6 O_2(g) \rightarrow ½ Al_2O_3(s) + 3/2 B_2O_3(s) + 6 H_2O(l)\]
Given the following additional data, calculate the enthalpy of formation of \(Al(BH_4)_3(g)\).
- \(Al_2O_3(s)\): \(\Delta H_f = -1669.8 \, kJ/mol\)
- \(B_2O_3(s)\): \(\Delta H_f = -1267.8 \, kJ/mol\)
- \(H_2O(l)\): \(\Delta H_f = -285.84 \, kJ/mol\)
- \(Al(BH_4)_3(l)\): \(\Delta H_{vap} = 30.125 \, kJ/mol\)
Q3.11
The standard enthalpy of formation (\(\Delta H_f^o\)) for water vapor is -241.82 kJ/mol at 25 °C. Use the data in the following table to calculate the value at 100 °C.
| Substance | \(C_p\) (J mol-1 K-1) |
|---|---|
| H2(g) | 28.84 |
| O2(g) | 29.37 |
| H2O(g) | 33.58 |
Q3.12
\(\Delta C_p = (1.00 + 2.00 \times 10^{-3} T)\, J/K\) and \(\Delta H_{298} = -5.00\, kJ\) for a dimerization reaction
\[2 A \rightarrow A_2\]
Find the temperature at which \(\Delta H = 0\).
Q3.13
From the following data, determine the lattice energy of \(BaBr_2\).
\[Ca(s) \rightarrow Ca(g)\]
with \(\Delta H_{sub} = 129\, kJ/mol\)
\[Br_2(l) \rightarrow Br_2(g)\]
with \(\Delta H_{vap} = 31\, kJ/mol\)
\[Br_2(g) \rightarrow 2 Br(g)\]
with \(D(Br-Br) = 193 \, kJ/mol\)
\[Ca(g) \rightarrow Ca^+(g) + e^-\]
with \(1^{st} \, IP(K) = 589.8 \, kJ/mol\)
\[Ca^+(g) \rightarrow Ca^{2+}(g) + e^-\]
with \(2^{nd} IP(K) = 1145.4 \,kJ/mol\)
\[Br(g) + e^- \rightarrow Br-(g) \]
with \(1^{st} EA(Br) = 194 \, kJ/mol\)
\[Ca(s) + Br_2^-(l) \rightarrow CaBr_2(s)\]
with \(\Delta H_f = -675 \, kJ/mol\)
Q3.15
Using average bond energies (Table T3) estimate the reaction enthalpy for the reaction
\[C_2H_4 + HBr \rightarrow C_2H_5Br\]
Contributors and Attributions
Patrick E. Fleming (Department of Chemistry and Biochemistry; California State University, East Bay)


