3.3: Reversible and Irreversible Pathways
- Page ID
- 84304
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The most common example of work in the systems discussed in this book is the work of expansion. It is also convenient to use the work of expansion to exemplify the difference between work that is done reversibly and that which is done irreversibly. The example of expansion against a constant external pressure is an example of an irreversible pathway. It does not mean that the gas cannot be re-compressed. It does, however, mean that there is a definite direction of spontaneous change at all points along the expansion.
Imagine instead a case where the expansion has no spontaneous direction of change as there is no net force push the gas to seek a larger or smaller volume. The only way this is possible is if the pressure of the expanding gas is the same as the external pressure resisting the expansion at all points along the expansion. With no net force pushing the change in one direction or the other, the change is said to be reversible or to occur reversibly. The work of a reversible expansion of an ideal gas is fairly easy to calculate.
If the gas expands reversibly, the external pressure (\(p_{ext}\)) can be replaced by a single value (\(p\)) which represents both the pressure of the gas and the external pressure.
\[ dw = -pdV \nonumber \]
or
\[ w = - \int p dV \nonumber \]
But now that the external pressure is not constant, \(p\) cannot be extracted from the integral. Fortunately, however, there is a simple relationship that tells us how \(p\) changes with changing \(V\) – the equation of state! If the gas is assumed to be an ideal gas
\[ w = - \int p dV -\int \left( \dfrac{nRT}{V}\right) dV \nonumber \]
And if the temperature is held constant (so that the expansion follows an isothermal pathway) the nRT term can be extracted from the integral.
\[ w = -nRT \int_{V_1}^{V_2} \dfrac{dV}{V} = -nRT \ln \left( \dfrac{V_2}{V_1} \right) \label{isothermal} \]
Equation \ref{isothermal} is derived for ideal gases only; a van der Waal gas would result in a different version.
What is the work done by 1.00 mol an ideal gas expanding reversibly from a volume of 22.4 L to a volume of 44.8 L at a constant temperature of 273 K?
Solution
Using Equation \ref{isothermal} to calculate this
\[\begin{align*} w & = -(1.00 \, \cancel{mol}) \left(8.314\, \dfrac{J}{\cancel{mol}\,\cancel{ K}}\right) (273\,\cancel{K}) \ln \left( \dfrac{44.8\,L}{22.4 \,L} \right) \nonumber \\[4pt] & = -1570 \,J = 1.57 \;kJ \end{align*} \]
Note: A reversible expansion will always require more work than an irreversible expansion (such as an expansion against a constant external pressure) when the final states of the two expansions are the same!
The work of expansion can be depicted graphically as the area under the p-V curve depicting the expansion. Comparing examples \(\PageIndex{1}\) and \(3.1.2\), for which the initial and final volumes were the same, and the constant external pressure of the irreversible expansion was the same as the final pressure of the reversible expansion, such a graph looks as follows.
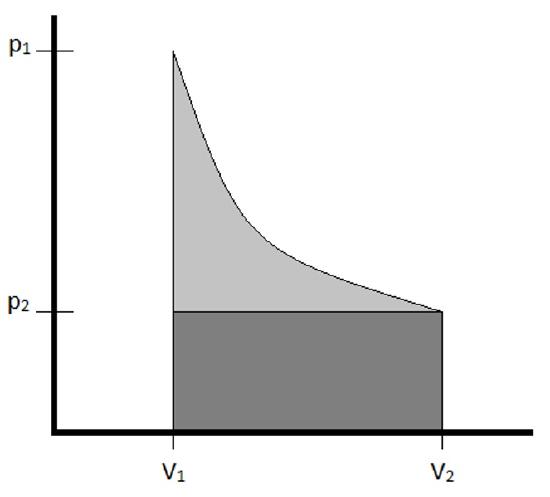
The work is depicted as the shaded portion of the graph. It is clear to see that the reversible expansion (the work for which is shaded in both light and dark gray) exceeds that of the irreversible expansion (shaded in dark gray only) due to the changing pressure of the reversible expansion. In general, it will always be the case that the work generated by a reversible pathway connecting initial and final states will be the maximum work possible for the expansion.
It should be noted (although it will be proven in a later chapter) that \(\Delta U\) for an isothermal reversible process involving only p-V work is 0 for an ideal gas. This is true because the internal energy, U, is a measure of a system’s capacity to convert energy into work. In order to do this, the system must somehow store that energy. The only mode in which an ideal gas can store this energy is in the translational kinetic energy of the molecules (otherwise, molecular collisions would not need to be elastic, which as you recall, was a postulate of the kinetic molecular theory!) And since the average kinetic energy is a function only of the temperature, it (and therefore \(U\)) can only change if there is a change in temperature. Hence, for any isothermal process for an ideal gas, \(\Delta U=0\). And, perhaps just as usefully, for an isothermal process involving an ideal gas, \(q = -w\), as any energy that is expended by doing work must be replaced with heat, lest the system temperature drop.
Constant Volume Pathways
One common pathway which processes can follow is that of constant volume. This will happen if the volume of a sample is constrained by a great enough force that it simply cannot change. It is not uncommon to encounter such conditions with gases (since they are highly compressible anyhow) and also in geological formations, where the tremendous weight of a large mountain may force any processes occurring under it to happen at constant volume.
If reversible changes in which the only work that can be done is that of expansion (so-called p-V work) are considered, the following important result is obtained:
\[ dU = dq + dw = dq - pdV \nonumber \]
However, \(dV = 0\) since the volume is constant! As such, \(dU\) can be expressed only in terms of the heat that flows into or out of the system at constant volume
\[ dU = dq_v \nonumber \]
Recall that \(dq\) can be found by
\[ dq = \dfrac{dq}{\partial T} dT = C\, dt \label{eq1} \]
This suggests an important definition for the constant volume heat capacity (\(C_V\)) which is
\[C_V \equiv \left( \dfrac{\partial U}{\partial T}\right)_V \nonumber \]
When Equation \ref{eq1} is integrated the
\[q = \int _{T_1}^{T_2} nC_V dt \label{isochoric} \]
Consider 1.00 mol of an ideal gas with \(C_V = 3/2 R\) that undergoes a temperature change from 125 K to 255 K at a constant volume of 10.0 L. Calculate \(\Delta U\), \(q\), and \(w\) for this change.
Solution
Since this is a constant volume process
\[w = 0 \nonumber \]
Equation \ref{isochoric} is applicable for an isochoric process,
\[q = \int _{T_1}^{T_2} nC_V dt \nonumber \]
Assuming \(C_V\) is independent of temperature:
\[\begin{align*} q & = nC_V \int _{T_1}^{T_2} dt \\[4pt] &= nC_V ( T_2-T_1) \\[4pt] & = (1.00 \, mol) \left( \dfrac{3}{2} 8.314\, \dfrac{J}{mol \, K}\right) (255\, K - 125 \,K) \\[4pt] & = 1620 \,J = 1.62\, kJ \end{align*} \]
Since this a constant volume pathway,
\[ \begin{align*} \Delta U & = q + \cancel{w} \\ & = 1.62 \,kJ \end{align*} \]
Constant Pressure Pathways
Most laboratory-based chemistry occurs at constant pressure. Specifically, it is exposed to the constant air pressure of the laboratory, glove box, or other container in which reactions are taking place. For constant pressure changes, it is convenient to define a new thermodynamic quantity called enthalpy.
\[ H \equiv U+ pV \nonumber \]
or
\[\begin{align*} dH &\equiv dU + d(pV) \\[4pt] &= dU + pdV + Vdp \end{align*} \]
For reversible changes at constant pressure (\(dp = 0\)) for which only p-V work is done
\[\begin{align} dH & = dq + dw + pdV + Vdp \\[4pt] & = dq - \cancel{pdV} + \cancel{pdV} + \cancelto{0}{Vdp} \\ & = dq \label{heat} \end{align} \]
And just as in the case of constant volume changes, this implies an important definition for the constant pressure heat capacity
\[C_p \equiv \left( \dfrac{\partial H}{\partial T} \right)_p \nonumber \]
Consider 1.00 mol of an ideal gas with \(C_p = 5/2 R\) that changes temperature change from 125 K to 255 K at a constant pressure of 10.0 atm. Calculate \(\Delta U\), \(\Delta H\), \(q\), and \(w\) for this change.
Solution
\[q = \int_{T_1}^{T_2} nC_p dT \nonumber \]
assuming \(C_p\) is independent of temperature:
\[ \begin{align*} q & = nC_p \int _{T_1}^{T_2} dT \\ & = nC_p (T_2-T_1) \\ & = (1.00 \, mol) \left( \dfrac{5}{2} 8.314 \dfrac{J}{mol \, K}\right) (255\, K - 125\, K) = 2700\, J = 1.62\, kJ \end{align*} \]
So via Equation \ref{heat} (specifically the integrated version of it using differences instead of differentials)
\[ \Delta H = q = 1.62 \,kJ \nonumber \]
\[ \begin{align*} \Delta U & = \Delta H - \Delta (pV) \\ & = \Delta H -nR\Delta T \\ & = 2700\, J - (1.00 \, mol) \left( 8.314\, \dfrac{J}{mol \, K}\right) (255\, K - 125 \,K) \\ & = 1620 \,J = 1.62\, kJ \end{align*} \]
Now that \(\Delta U\) and \(q\) are determined, then work can be calculated
\[\begin{align*} w & =\Delta U -q \\ & = 1.62\,kJ - 2.70\,kJ = -1.08\;kJ \end{align*} \]
It makes sense that \(w\) is negative since this process is an gas expansion.
Calculate \(q\), \(w\), \(\Delta U\), and \(\Delta H\) for 1.00 mol of an ideal gas expanding reversibly and isothermally at 273 K from a volume of 22.4 L and a pressure of 1.00 atm to a volume of 44.8 L and a pressure of 0.500 atm.
Solution
Since this is an isothermal expansion, Equation\ref{isothermal} is applicable
\[ \begin{align*} w & = -nRT \ln \dfrac{V_2}{V_1} \\ & = (1.00 \, mol) \left( 8.314\, \dfrac{J}{mol \, K}\right) (255\, K) \ln \left(\dfrac{44.8\,L}{22.4\,L} \right) \\ & = 1572\,J = 1.57\,kJ \\[4pt] \Delta U & = q + w \\ & = q + 1.57\,KJ \\ & = 0 \\[4pt] q &= -1.57\,kJ \end{align*} \]
Since this is an isothermal expansion
\[\Delta H = \Delta U + \Delta (pV) = 0 + 0 \nonumber \]
where \(\Delta (pV) = 0\) due to Boyle’s Law!
Adiabatic Pathways
An adiabatic pathway is defined as one in which no heat is transferred (\(q = 0\)). Under these circumstances, if an ideal gas expands, it is doing work (\(w < 0\)) against the surroundings (provided the external pressure is not zero!) and as such the internal energy must drop (\(\Delta U <0 \)). And since \(\Delta U\) is negative, there must also be a decrease in the temperature (\(\Delta T < 0\)). How big will the decrease in temperature be and on what will it depend? The key to answering these questions comes in the solution to how we calculate the work done.
If the adiabatic expansion is reversible and done on an ideal gas,
\[dw = -pdV \nonumber \]
and
\[dw = nC_vdT \label{Adiabate2} \]
Equating these two terms yields
\[- pdV = nC_v dT \nonumber \]
Using the ideal gas law for an expression for \(p\) (\(p = nRT/V\))
\[ - \dfrac{nRT}{V} dV = nC_vdT \nonumber \]
And rearranging to gather the temperature terms on the right and volume terms on the left yields
\[\dfrac{dV}{V} = -\dfrac{C_V}{R} \dfrac{dT}{T} \nonumber \]
This expression can be integrated on the left between \(V_1\) and \(V_2\) and on the right between \(T_1\) and \(T_2\). Assuming that \(C_v/nR\) is independent of temperature over the range of integration, it can be pulled from the integrand in the term on the right.
\[ \int_{V_1}^{V_2} \dfrac{dV}{V} = -\dfrac{C_V}{R} \int_{T_1}^{T_2} \dfrac{dT}{T} \nonumber \]
The result is
\[ \ln \left(\dfrac{V_2}{V_1} \right) = - \dfrac{C_V}{R} \ln \left( \dfrac{T_2}{T_1} \right) \nonumber \]
or
\[ \left(\dfrac{V_2}{V_1} \right) = \left(\dfrac{T_2}{T_1} \right)^{- \frac{C_V}{R}} \nonumber \]
or
\[ V_1T_1^{\frac{C_V}{R}} = V_2T_2^{\frac{C_V}{R}} \nonumber \]
or
\[T_1 \left(\dfrac{V_1}{V_2} \right)^{- \frac{R} {C_V}} = T_2 \label{Eq4Alternative} \]
Once \(\Delta T\) is known, it is easy to calculate \(w\), \(\Delta U\) and \(\Delta H\).
1.00 mol of an ideal gas (CV = 3/2 R) initially occupies 22.4 L at 273 K. The gas expands adiabatically and reversibly to a final volume of 44.8 L. Calculate \(\Delta T\), \(q\), \(w\), \(\Delta U\), and \(\Delta H\) for the expansion.
Solution
Since the pathway is adiabatic:
\[q =0 \nonumber \]
Using Equation \ref{Eq4Alternative}
\[ \begin{align*} T_2 & = T_1 \left(\dfrac{V_1}{V_2} \right)^{- \frac{R} {C_V}} \\ & =(273\,K) \left( \dfrac{22.4\,L}{44.8\,L} \right)^{2/3} \\ & = 172\,K \end{align*} \]
So
\[\Delta T = 172\,K - 273\,K = -101\,K \nonumber \]
For calculating work, we integrate Equation \ref{Adiabate2} to get
\[ \begin{align*} w & = \Delta U = nC_v \Delta T \\ & = (1.00 \, mol) \left(\dfrac{3}{2} 8.314\, \dfrac{J}{mol \, K} \right) (-101\,K ) \\ & = 1.260 \,kJ \end{align*} \]
\[ \begin{align*} \Delta H & = \Delta U + nR\Delta T \\ & = -1260\,J + (1.00 \, mol) \left(\dfrac{3}{2} 8.314\, \dfrac{J}{mol \, K} \right) (-101\,K ) \\ & = -2100\,J \end{align*} \]
The following table shows recipes for calculating \(q\), \(w\), \(\Delta U\), and \(\Delta H\) for an ideal gas undergoing a reversible change along the specified pathway.
| Pathway | \(q\) | \(w\) | \(\Delta U\) | \(\Delta H\) |
|---|---|---|---|---|
| Isothermal | \(nRT \ln (V_2/V_1) \) | \(-nRT \ln (V_2/V_1) \) | 0 | 0 |
| Isochoric | \(C_V \Delta T\) | 0 | \(C_V \Delta T\) | \(C_V \Delta T + V\Delta p\) |
| Isobaric | \(C_p \Delta T\) | \(- p\Delta V\) | \(C_p \Delta T - p\Delta V\) | \(C_p \Delta T\) |
| adiabatic | 0 | \(C_V \Delta T\) | \(C_V \Delta T\) | \(C_p \Delta T\) |


