13.4: Properties of Determinants
- Page ID
- 106885
1-
\[\label{eq:identity} \begin{vmatrix} 1 &0&0 \\ 0&1 &0 \\ 0& 0 &1 \end{vmatrix}=1\]
This is true in any dimension, and can be understood easily from geometrical arguments. In two dimensions, the columns represent unitary vectors along the \(x\) and \(y\) axis, and the parallelogram is therefore a square of unit area. In three dimensions, the columns represent unitary vectors along the \(x\), \(y\) and \(z\) axis, and the box is therefore a cube of unit volume.
2-
Antisymmetry: If two rows (or two columns) of a determinant are interchanged, the value of the determinant is multiplied by -1. This property is extremely useful in quantum mechanics, so it is worth remembering!
\[\label{eq:determinants4} \begin{vmatrix} a &b & c \\ d &e &f \\ g &h &i \end{vmatrix}=- \begin{vmatrix} b&a &c \\ e&d &f\\ h &g &i \end{vmatrix}=- \begin{vmatrix} d&e &f \\ a &b &c\\ g &h &i \end{vmatrix}\]
We already discussed this property in two dimensions (see Figure \(13.3.3\)).
3-
Scalars can be factored out from rows and columns.
\[\label{eq:determinants5} \begin{vmatrix} a&b &c \\ \lambda d &\lambda e &\lambda f\\ g &h&i \end{vmatrix} = \lambda \begin{vmatrix} a &b & c \\ d &e &f \\ g &h &i \end{vmatrix}\]
Geometrically speaking, if you multiply the length of one of the edges of the parallelepiped by \(\lambda\), the volume is also multiplied by \(\lambda\).
4-
Addition rule: If all the elements of any row (or column) are written as the sum of two terms, then the determinant can be written as the sum of two determinants
\[\label{eq:determinants6} \begin{vmatrix} a+b&c &d \\ e+f &g &h\\ i+j &k &l \end{vmatrix} = \begin{vmatrix} a&c & d \\ e& g &h\\ i&k &l \end{vmatrix} + \begin{vmatrix} b&c &d \\ f& g &h\\ j&k &l \end{vmatrix}\]
\[\label{eq:determinants6b} \begin{vmatrix} a+b&c+d &e+f \\ g &h &i\\ j &k &l \end{vmatrix}= \begin{vmatrix} a&c & e \\ g &h &i\\ j &k &l \end{vmatrix}+ \begin{vmatrix} b&d &f \\ g &h &i\\ j &k &l \end{vmatrix}\]
5-
The value of a determinant is zero if two rows or two columns are equal. This is a consequence of property 2. Exchanging the two identical rows is supposed to change the sign of the determinant, but we know that exchanging two identical rows does nothing to the determinant. Therefore, the determinant has to be zero.
Geometrically, two edges of the box would be the same, rendering a flat box with no volume.
\[\label{eq:determinants3} \begin{vmatrix} {\color{red}a} &{\color{Red}a} &{\color{Blue} b} \\ {\color{red}c} &{\color{red}c} &{\color{Blue}d} \\ {\color{red}e} &{\color{red}e} &{\color{Blue}f} \end{vmatrix}=0\]
6-
The value of a determinant is unchanged if one row or column is added or subtracted to another. This property is a consequence of properties 4 and 5:
\[\label{eq:determinants7} \begin{vmatrix} a+b&b &c \\ d+e & e & f\\ g+h &h &i \end{vmatrix}= \begin{vmatrix} a&b &c \\ d&e& f\\ g&h&i \end{vmatrix}+ \begin{vmatrix} b&b&c \\ e&e& f\\ h&h&i \end{vmatrix}\]
7-
A special case of property 3 is that if all the elements of a row or column are zero, the value of the determinant is zero. In geometrical terms, if one of the edges is a point, the volume is zero.
\[\label{eq:determinants6extra} \begin{vmatrix} a &b &c \\ 0 &0 &0 \\ d &e &f \end{vmatrix}=0\]
8-
The value of a determinant is zero if one row (or column) is a multiple of another row (or column). Geometrically, this means that two edges of the parallelepiped lie on the same line, and therefore the volume is zero. This is a consequence of properties 3 and 5:
\[\label{eq:determinants8} \begin{vmatrix} a&b &c \\ \lambda a &\lambda b &\lambda c\\ d &e &f \end{vmatrix}= \lambda\begin{vmatrix} a&b & c\\ a &b&c \\ d&e &f \end{vmatrix}=0\]
9-
Transposition: the value of the determinant is unchanged if its rows and columns are interchanged. This property can be derived from the previous properties, although it is a little complicated for the level of this course.
\[\label{eq:determinants2} \begin{vmatrix} {\color{red}a}&{\color{OliveGreen}b} &{\color{Blue} c} \\ {\color{red}d} &{\color{OliveGreen}e} &{\color{Blue}f} \\ {\color{red}g} &{\color{OliveGreen}h} &{\color{Blue}i} \end{vmatrix}= \begin{vmatrix} {\color{red}a} &{\color{red}d} &{\color{red}g} \\ {\color{OliveGreen}b} &{\color{OliveGreen}e} &{\color{OliveGreen}h} \\ {\color{Blue}c}& {\color{Blue}f}&{\color{Blue}i} \end{vmatrix}\]
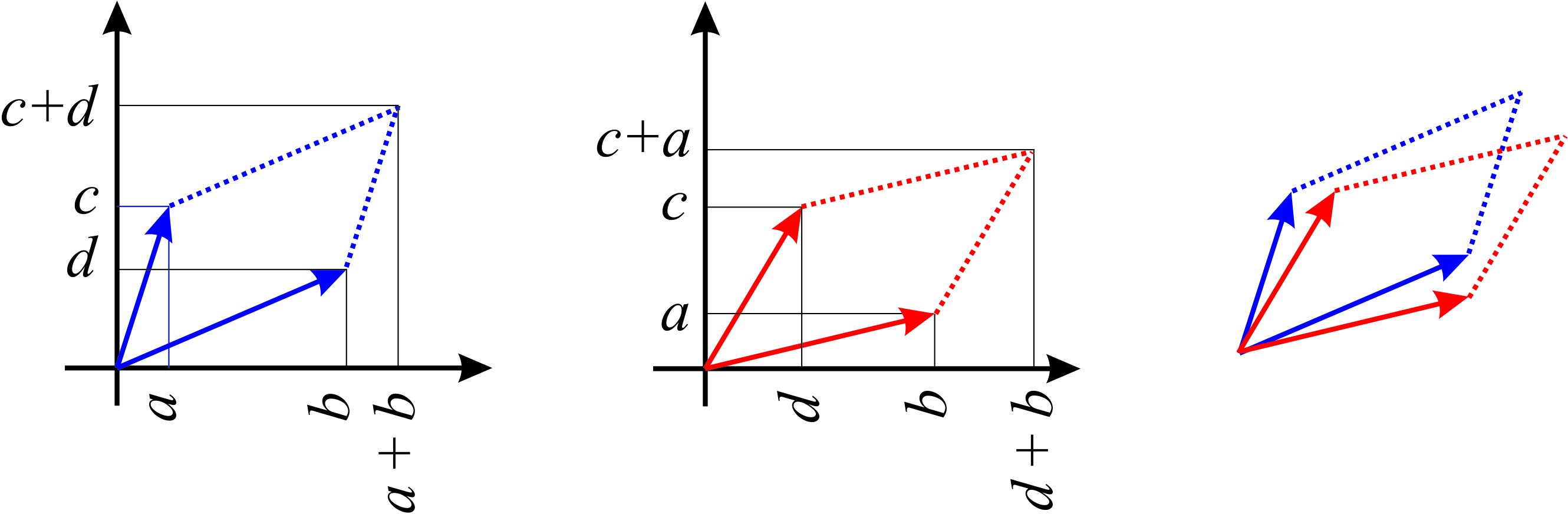
Geometrically, interchanging rows by columns rotates the parallelogram (or the box in 3D) without changing the area (or volume). Figure \(\PageIndex{1}\) shows that
\[\begin{vmatrix}b &a\\ d& c \end{vmatrix}=\begin{vmatrix}b &d\\ a& c \end{vmatrix} \nonumber\]
Determine the value of the following determinant by inspection.
\[\begin{vmatrix} 2&6 &1 \\ -4 &4 &-2\\ 2 &-3 &1 \end{vmatrix} \nonumber\]
Solution
We notice that the third column is a multiple of the first:
\[\begin{align*} \begin{vmatrix} 2&6 &1 \\ -4 &4 &-2\\ 2 &-3 &1 \end{vmatrix} &= \begin{vmatrix} 1\times 2&6 &1 \\ -2 \times 2 &4 &-2\\ 1 \times 2 &-3 &1 \end{vmatrix} \\[4pt] &=2\times \begin{vmatrix} 1&6 &1 \\ -2 &4 &-2\\ 1 &-3 &1 \end{vmatrix} \\[4pt] &=\displaystyle{\color{Maroon}0} \end{align*} \nonumber\]
The determinant is zero because two of its columns are the same.