7.2: Fourier Series
- Page ID
- 106842
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A Fourier series is a linear combination of sine and cosine functions, and it is designed to represent periodic functions:
\[\label{eq:fourier} f(x)=\dfrac{a_0}{2}+\sum_{n=1}^{\infty}a_n \cos\left ( \dfrac{n\pi x}{L} \right )+\sum_{n=1}^{\infty}b_n \sin\left ( \dfrac{n\pi x}{L} \right ) \]
The coefficients \(a_0, a_1,a_2...a_n\) and \(b_1, b_2....b_n\) are constants.
It is important to notice that the period of the sine and cosine functions in Equation \ref{eq:fourier} is \(P=2L/n\) (see Section 1.4). This means that we will be mixing sines and cosines of periods \(2L\), \(2L/2\), \(2L/3\), \(2L/4\), etc. As we will see, this linear combination will result in a periodic function of period \(P = 2L\).
In addition, we need only the odd terms (the sine functions) to represent an odd periodic function, so in this case all the \(a_n\) coefficients (including \(a_0\)) will be zero. We need only even terms (the cosine functions) to represent an even function, so in this case all the \(b_n\) coefficients will be zero. Why don’t we have a \(b_0\) term? This is because \(\sin{(0)}=0\). In the case of the cosine terms, the \(n=0\) term is separated from the sum, but it does not vanish because \(\cos{(0)}\neq0\).
This means that an odd periodic function with period \(P=2L\) will be in general:
\[f(x)= b_1 \sin{\left(\dfrac{\pi x}{L}\right)}+b_2 \sin{\left(\dfrac{2\pi x}{L}\right)}+b_3 \sin{\left(\dfrac{3\pi x}{L}\right)}... \nonumber \]
Let’s say we want to construct an odd periodic function of period \(P=2\pi\). Because the period is \(2L\), this means that \(L=\pi\):
\[f(x)= b_1 \sin{\left(x\right)}+b_2 \sin{\left(2x\right)}+b_3 \sin{\left(3x\right)}... \nonumber \]
We in fact already saw an example like this in Figure \(7.1.2\) (right). This periodic function, which is constructed using \(b_n=1/n\), has a period of \(2\pi\) as we just predicted. Let’s see other examples with different coefficients:
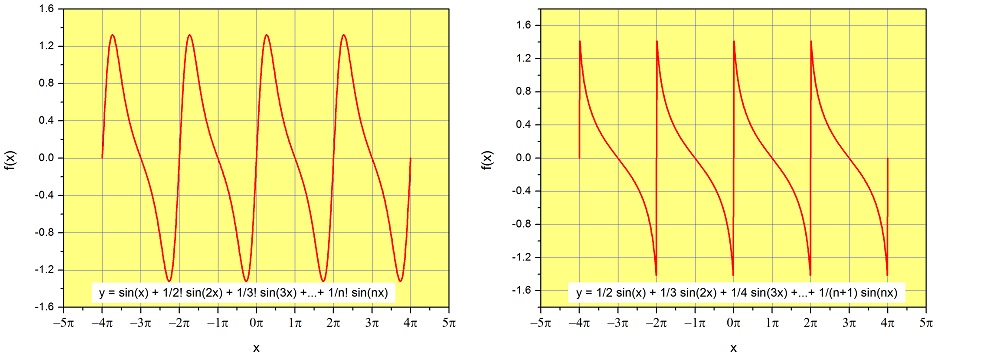
Notice that we are mixing the functions \(\sin{\left(x\right)}, \sin{\left(2x\right)},\sin{\left(3x\right)}...\) using different coefficients, and always create a periodic function with period \(P=2\pi\).
Coming back to Equation \ref{eq:fourier}, we know that different coefficients will create different periodic functions, but they will all have a period \(2L\). The obvious question now is how to calculate the coefficients that will create the function we want. Let’s say that the periodic function is constructed by a periodic extension of the function \(f(x)\), which is defined in the interval \([-L,L]\). One example would be the function of Figure \(7.1.5\), which is defined in the interval \([-\pi,\pi]\). If we create the periodic extension of this function, we will create a periodic function with period \(2\pi\). Analogously, by creating a periodic extension of a function defined in the interval \([-L,L]\) we will create a periodic function with period \(2L\). The coefficients of Equation \ref{eq:fourier} are calculated as follows:
\[\label{ao} a_0=\dfrac{1}{L}\int_{-L}^{L}f(x)dx \]
\[\label{an} a_n=\dfrac{1}{L}\int_{-L}^{L}f(x)\cos{\left(\dfrac{n\pi x}{L} \right)}dx \]
\[\label{bn} b_n=\dfrac{1}{L}\int_{-L}^{L}f(x)\sin{\left(\dfrac{n\pi x}{L} \right)}dx \]
Notice that Equation \ref{ao} is a special case of Equation \ref{an}, and that we don’t have a coefficient \(b_0\) because \(\sin{(0)}=0\). Because Equation \ref{eq:fourier} represents a periodic function with period \(2L\), the integration is performed over one period centered at zero (that is, \(L\) is half the period).
Equation \ref{eq:fourier} is often written as:
\[\label{eq:fourier_alt} f(x)=a_0+\sum_{n=1}^{\infty}a_n \cos\left ( \dfrac{n\pi x}{L} \right )+\sum_{n=1}^{\infty}b_n \sin\left ( \dfrac{n\pi x}{L} \right ) \]
If we choose to do this, we of course need to re-define the coefficient \(a_0\) as:
\[a_0=\dfrac{1}{2L}\int_{-L}^{L}f(x)dx. \nonumber \]
Both versions give of course the same series, and whether you choose one or the other is a matter of taste. You may see the two versions in different textbooks, so don’t get confused!.
Obtain the Fourier series of the periodic function represented in the figure.

Solution
\(y(x)\) is a periodic function with period \(P=2\). It can be constructed by the periodic extension of the function \(f(x)=2x\), defined in the interval \([-1,1]\). Notice that this interval has a width equal to the period, and it is centered at zero.
Because \(y(x)\) is odd, we will not bother calculating the coefficients \(a_n\). We could, but we would obtain zero for all of them. Equation \ref{eq:fourier}, therefore, reduces to:
\[y(x)=\sum\limits_{n=1}^{\infty}b_n sin\left ( \dfrac{n\pi x}{L} \right ) \nonumber \]
From Equation \ref{bn}, the coefficients \(b_n\) are calculated as:
\[b_n=\dfrac{1}{L}\int_{-L}^{L}f(x)\sin{\left(\dfrac{n\pi x}{L} \right)}dx \nonumber \]
and in this case, because \(L=1\) (half the period),
\[b_n=\int_{-1}^{1}(2x)\sin{\left(n\pi x \right)}dx=2\int_{-1}^{1}x\sin{\left(n\pi x \right)}dx \nonumber \]
The primitive of \(\int x\sin{\left(a x \right)}dx\) is \(\dfrac{\sin{(ax)}}{a^2}-\dfrac{x \cos{(ax)}}{a}\) (see formula sheet), so
\[b_n=2\int_{-1}^{1}x\sin{\left(n\pi x \right)}dx=2\left[\dfrac{\sin{(n \pi)}}{(n\pi)^2}-\dfrac{\cos{(n\pi)}}{n \pi}-\left(\dfrac{\sin{(n \pi (-1))}}{(n\pi)^2}-\dfrac{(-1) \cos{(n\pi (-1))}}{n \pi}\right)\right] \nonumber \]
Using the fact that \(\sin{(n\pi)}\) is zero and \(\cos{x}\) is an even function:
\[b_n=-4\dfrac{ \cos{(n\pi)}}{n \pi} \nonumber \]
Let’s write a few terms in a table:
| \(n\) | \(\cos{(n\pi)}\) | \(b_n\) |
|---|---|---|
| 1 | -1 | \(\dfrac{4}{\pi}\) |
| 2 | 1 | \(-\dfrac{4}{2\pi}\) |
| 3 | -1 | \(\dfrac{4}{3\pi}\) |
| 4 | 1 | \(-\dfrac{4}{4\pi}\) |
| 5 | -1 | \(\dfrac{4}{5\pi}\) |
A general expression for \(b_n\) is:
\[b_n=4 \dfrac{(-1)^{n+1}}{n\pi} \nonumber \]
The series
\[y(x)=\sum_{n=1}^{\infty}b_n sin\left ( \dfrac{n\pi x}{L} \right ) \nonumber \]
is then:
\[\label{eq:sawtooth} \displaystyle{\color{Maroon}y(x)=\dfrac{4}{\pi}\sum_{n=1}^{\infty}\dfrac{(-1)^{n+1}}{n} sin\left (n\pi x \right )} \]
As in the case of a Taylor series, Equation \ref{eq:sawtooth} is exact if we include the infinite terms of the series. If we truncate the series using a finite number of terms, we will create an approximation. Figure \(\PageIndex{1}\) shows an example with 1, 2, 3 and 8 terms.

Obtain the Fourier series of the square wave formed by the periodic extension of the function:
\[f(x)=\left\{\begin{matrix}0 & -\pi\leq x\leq 0 \\ 1 &0<x\leq \pi \end{matrix}\right. \nonumber \]
Solution
The periodic extension of the function \(f(x)\) produces a periodic function with period \(2\pi\):
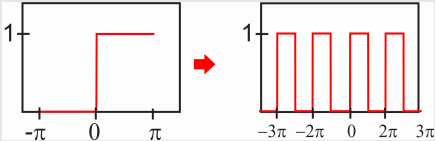
Strictly speaking, the resulting periodic function is neither even nor odd, so we would need to calculate all the coefficients. However, you may notice that the function would be odd if we were to subtract 1/2 from all points. In other words, the periodic function we are looking for will be a constant (\(a_0\)) plus an odd periodic function (sine series). We will calculate the constant, but from this discussion it should be obvious that we will get \(a_0/2=1/2\). We will also calculate the rest of the \(a_n\) coefficients, but we now know they will all be zero.
The first coefficient, \(a_0\) is (Equation \ref{ao}):
\[a_0=\dfrac{1}{L}\int_{-L}^{L}f(x)dx \nonumber \]
Here, \(L=\pi\) (half the period), so:
\[a_0=\dfrac{1}{\pi}\int_{-\pi}^{\pi}f(x)dx=\dfrac{1}{\pi}\int_{0}^{\pi}1dx=1 \nonumber \]
where we have used the fact that \(f(x)=0\) in the interval \(-\pi<x<0\). The coefficients \(a_n\) are (Equation \ref{an})
\[a_n=\dfrac{1}{L}\int_{-L}^{L}f(x)\cos{\left(\dfrac{n\pi x}{L} \right)}dx=\dfrac{1}{\pi}\int_{0}^{\pi}\cos{\left(n x \right)}dx=\dfrac{1}{\pi}\left.\begin{matrix}\left ( \dfrac{sin(n\pi))}{n} \right )\end{matrix}\right|_0^\pi=0 \nonumber \]
The coefficients \(b_n\) are (Equation \ref{bn})
\[b_n=\dfrac{1}{L}\int_{-L}^{L}f(x)\sin{\left(\dfrac{n\pi x}{L} \right)}dx=\dfrac{1}{\pi}\int_{0}^{\pi}\sin{\left(n x \right)}dx=\dfrac{1}{\pi}\left.\begin{matrix}\left ( -\dfrac{cos(n\pi))}{n} \right )\end{matrix}\right|_0^\pi=-\dfrac{1}{\pi n}(\cos{(n\pi)}-cos{(0)})=\dfrac{1-\cos{(n\pi)}}{n\pi} \nonumber \]
Let’s see a few terms in a table:
| \(n\) | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| \(\cos{(n\pi)}\) | -1 | 1 | -1 | 1 | -1 | 1 |
| \(b_n\) | \(\dfrac{2}{\pi}\) | \(0\) | \(\dfrac{2}{3\pi}\) | \(0\) | \(\dfrac{2}{5\pi}\) | 0 |
The series is (Equation \ref{eq:fourier})
\[f(x)=\dfrac{a_0}{2}+\sum_{n=1}^{\infty}a_n cos\left( \dfrac{n\pi x}{L} \right)+\sum_{n=1}^{\infty}b_n sin\left( \dfrac{n\pi x}{L} \right) \nonumber \]
and with the coefficients we got we can write:
\[f(x)=\dfrac{1}{2}+\dfrac{2}{\pi}\sin{(x)}+\dfrac{2}{3\pi}\sin{(3x)}+\dfrac{2}{5\pi}\sin{(5x)}... \nonumber \]
or more elegantly:
\[\displaystyle{\color{Maroon}\dfrac{1}{2}+\dfrac{2}{\pi} \sum_{n=0}^{\infty}\dfrac{1}{2n+1}\sin{[(2n+1)x]}} \nonumber \]
Notice that, as expected, we have a sine series (which represents and odd periodic function) plus a constant (which ’pushes’ the function up).
Need help? The links below contain solved examples.
External links:
- Fourier series example I: http://www.youtube.com/watch?v=jzzpxqVohhI
- Fourier series example II: http://www.youtube.com/watch?v=edwG9x5v3Xo


