11.E: Quantum Mechanics and Atomic Structure (Exercises)
- Page ID
- 41337
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Q11.1
What is the wavelength associated with a photon of a light with the energy is \(3.6 \times 10^{-19}\;J\)?
S11.1
\[E= hv = \dfrac{hc}{λ} \nonumber \]
\[3.6 \times 10^{-19}\; J = \dfrac{(6.626 \times 10^{-34}\; J\;s) ( 3 \times 10^8\; ms^{-1})}{\lambda}\nonumber \]
\[λ = 0.55 \times 10^{-7}\; m = 550\; nm\nonumber \]
Q11.2
Calculate the energy of a photon of a light with the frequency is \(6.5 \times 10^{-14}\; s^{-1}\) ?
S11.2
\[E= hv\nonumber \]
\[E=( 6.626 \times 10^{-34}J\;s) ( 6.5 \times 10^{-14} s^{-1})\nonumber \]
\[E= 4.3 \times 10^{-19}\;J\nonumber \]
Q11.3a
What are the wavelength of the light emitted by atomic hydrogen when the electron move from \(n=5\) to \(n=3\) orbit in the Bohr model?
S11.3a
Bohr model:
\[\dfrac{1}{λ} = R_H \left(\dfrac{1}{n_a^2} -\dfrac{1}{n_b^2} \right)\nonumber \]
\[\dfrac{1}{λ} = ( 1.09678 \times 10^{-2} nm^{-1} ) \left(\dfrac{1}{9}- \dfrac{1}{25}\right) \nonumber \]
\[λ = 1,282\; nm\nonumber \]
Q11.3b
Calculate the different energy between \(n=3\) and \(n=4\) of atomic hydrogen based on Bohr orbits
S11.3b
\[\Delta E=-hcR_H \left(\dfrac{1}{3^2}\ - \dfrac{1}{4^2} \right) \nonumber \]
\[\Delta E=-6.626 \times 10^{-34} J.s)(2.9979 \times 10^8\; m/s)(109,737\; cm^{-1}) \left(\dfrac{1}{3^2} - \dfrac{1}{4^2}\right))\nonumber \]
\[\Delta E= 1.8 \times 10^{-21}\; J\nonumber \]
Q11.4
Calculate the wavenumber of the wavelength of the light emitted from the \(n=8\) to \(n=6\) transition.
S11.4
This is a simple application of the Rydberg equation
\[ \tilde{\nu} R_H \left (\dfrac{1}{n_{f}^{2}} -\dfrac{1}{n_{i}^{2}} \right)\nonumber \]
with \(n_i = 6\) and \(n_f = 8\).
\[ \tilde{\nu}=109,737cm^{-1}\left (\dfrac{1}{6^{2}}-\dfrac{1}{8^{2}} \right)=1333.61 \; cm^{-1}\nonumber \]
Q11.5
Calculate the wavelength associated with a 42 g baseball with speed of 80 m/s.
S11.5
\[ \lambda =\dfrac{h}{p} = \dfrac{h}{mv}\nonumber \]
\[ \lambda = \dfrac{6.626 \times 10^{34} J s}{(0.042 \; kg)( 80 m/s)} = 1.97 \times 10^{-34} \, m\nonumber \]
This is a very small wavelength as expected since a ball behaves rather classically (i.e., non-quantum).
Q11.6
Calculate the energy of a 530-nm photon.
S11.6
\[p =\dfrac{E}{c}\nonumber \]
\[\lambda = \dfrac{h}{p}\nonumber \]
\[\lambda = \dfrac{hc}{E}\nonumber \]
\[ E= \dfrac{hc}{\lambda} = \dfrac{(6.626 \times 1-^{-34})( 3 \times 10^{8})}{530 \times 10^{-9}} = 3.75 \times 10^{-9} \; J\nonumber \]
11.3: The Photoelectric Effect
Q11.7
Describe Planck's three experimental observations that explain the photoelectric effect.
S11.7
"When light of a certain frequency shines on a clean metal surface, electrons are ejectedd from the metal. Experimentally, it is found that:
- The number of electrons ejected is proportional to the intensity of light
- The kinetic energy of the ejected electrons is proportional to the frequency of the ejected light
- No electrons can be ejected if the frequency of the light is lower than a certain value, called the threshold frequency (\(nu_o\)).
Q11.8a
What is the difference between classical and quantum mechanics? Provide the equation relating the energy of emitted radiation to frequency.
S11.8a
Classical mechanics predicts that the radiant energy produced by oscillating objects is continuous. Quantum mechanics predicts that their energy can be viewed as existing in discrete levels. The equation is \[E = h\nu\nonumber \]. Energy is emitted in discrete multiples of \(h\nu\), where h = Planck's constant.
Q11.8b
Do you expect the first ionization of an atom to be an endothermic process or an exothermic process?
S11.8b
It will be endothermic because energy is needed to ionize the atom.
Q11.9a
Calculate the wavelength of light with an energy of \(5.22 \times 10^{-19}\; J\).
S11.9a
Rearrange the equation \[E = \dfrac{hc}{\lambda }\nonumber \] so that the unknown value is the wavelength of light \[\lambda = \dfrac{hc}{E}\nonumber \] \[\lambda =\dfrac{(6.626\times 10^{-34}Js)(3.0\times 10^{8}m/s)}{5.22\times 10^{-19}J} = 3.81\times 10^{-7}m = 381 nm\nonumber \]
Q11.9b
You realize after class that you forgot to write down the final wavelength of your proton. You do, however, remember that the potential difference was 114 V. From this information, figure out the final wavelength:
S11.9b
\(\frac{1}{2}mv^{2}=eV\)
Q11.10a
given the uncertainty for position of an electron circling an atom is 0.5A0. Find uncertainty in its velocity?
S11.10a
Δp ≥ h/ 4πΔx = 6.626 x 10-34 Js/ 4π(0.5 x 10-10m) = 1.311.05 x 10-24kg m s-1
Δ v= Δp/ m ≥ 1.3 x 10-24 kg m s-1/ 9.109 x 10-31 kg = 1 x 106 m s-1
Q11.10
If the uncertainty of measuring the position of an electron is 2.0 Å, what is the uncertainty of simultaneously measuring its velocity? Hint: What formula deals with uncertainty of measurements?
11.7: The Schrödinger Wave Equation
Q11.11
A typical mass for a horse is 510 kg, and a typical galloping speed is 22 kilometers per hour. Use these values to answer the following questions.
- What is the momentum of a galloping horse? What is its wavelength?
- If a galloping horse's velocity and position are simultaneously measured, and the velocity is measured to within ± 1.0%, what is the uncertainty of its position?
- Suppose Planck's constant was actually 0.01 J s. How would that change your answers to (a) and (b)? Which values would be unchanged?
Hints:
- de Broglie's postulate deals with the wave-like properties of particles.
- Heisenberg's uncertainty principle deals with uncertainty of simultaneous measurements.
S11.11
(a)
1. Use the relationship between velocity and momentum to find the momentum.
\[ p = m v \nonumber \]
\[ p = 510\ kg \times 22\ \dfrac{km}{hr} \times \dfrac{1000\ m}{km} \times \dfrac{hr}{3600\ s} \nonumber \]
\[ p = 3.1 \times 10^3\ \dfrac{kg\ m}{s} \nonumber \]
2. Find the de Broglie wavelength.
\[ \lambda = \dfrac{h}{p} \nonumber \]
\[ \lambda = \dfrac{6.626 \times 10^{-34}\ J\ s}{3.1 \times 10^3\ \dfrac{kg\ m}{s}} \times \dfrac{\dfrac{kg\ m^2}{s^2}}{J} \nonumber \]
\[ \lambda = 2.1 \times 10^{-37}\ m \nonumber \]
(b)
1. Find the uncertainty of momentum from the uncertainty of velocity.
\[ \Delta p = m \Delta v \nonumber \]
\[ \Delta v = 0.01 \times v \nonumber \]
\[ \Delta p = 510\ kg \times 0.01 \times 22\ \dfrac{km}{hr} \times \dfrac{1000\ m}{km} \times \dfrac{hr}{3600\ s} \nonumber \]
\[ \Delta p = 31 \dfrac{kg\ m}{s} \nonumber \]
2. Use Heisenberg's uncertainty principle to find the uncertainty of position.
\[ \Delta x \Delta p \geq \dfrac{h}{4 \pi} \nonumber \]
\[ \Delta x \geq \dfrac{h}{4 \pi \Delta p} \nonumber \]
\[ \Delta x \geq \dfrac{6.626 \times 10^{-34}\ J\ s}{4 \pi \times 3.1 \times 10^3 \dfrac{kg\ m}{s}} \times \dfrac{\dfrac{kg\ m^2}{s^2}}{J} \nonumber \]
\[ \Delta x \geq 1.7 \times 10^{-36}\ m \nonumber \]
(c)
The calculations that involve Planck's constant (h) will change. This much larger value will make the wave-like properties of the horse more important; its wavelength and uncertainty of position will increase dramatically:
\[ \lambda ' = \dfrac{h'}{p} = \dfrac{0.010\ J\ s}{3.1 \times 10^3\ \dfrac{kg\ m}{s} \times \dfrac{\dfrac{kg\ m^2}{s^2}}{J}} \nonumber \]
\[ \lambda ' = 3.2 \times 10^{-6}\ m = 3200\ nm \nonumber \]
\[ \Delta x' \geq \dfrac{h'}{4 \pi \Delta p} = \dfrac{0.010\ J\ s}{4 \pi \times 3.1 \times 10^3 \dfrac{kg\ m}{s}} \times \dfrac{\dfrac{kg\ m^2}{s^2}}{J} \nonumber \]
\[ \Delta x' \geq 2.6 \times 10^{-5} m = 26\ \mu m \nonumber \]
The momentum would not change.
Q11.12a
how fast must a person weighing 42 kg move through a door 0.5 m wide in order to be diffracted?
S11.12a
p= h/ λ = 6.626 x 10 -34 J s/ 0.5
= 3.313 x 10-34 kg m s-1
V= p/m = 3.313 x 10-34 / 42 kg = 7.88 x 10-36 ms-1
Q11.12b
When a particle passes through a slit, diffraction occurs if the particle's wavelength is on the same order of magnitude as the width of the slit. At approximately what velocity would a 1670 kg car have to move through the Lincoln Tunnel (6.6 m width) for diffraction to occur? Hint: How can you find the wavelength of the car?
S11.12b
1. Use de Broglie's equation to relate velocity to wavelength; solve for velocity.
\[ \lambda = \dfrac{h}{m v} \nonumber \]
\[ v = \dfrac{h}{m \lambda} \nonumber \]
2. Set the wavelength equal to the tunnel width and solve.
\[ v = \dfrac{6.626 \times 10^{-34}\ J\ s}{1670\ kg \times 6.6\ m} \times \dfrac{\dfrac{kg\ m^2}{s^2}}{J} \nonumber \]
Answer: the car would have to be driving very slowly.
\[ v = 6.0 \times 10^{-38}\ m/s \nonumber \]
Q11.13a
The Paschen emission spectrum is the collection of spectral lines emitted by H atoms, where the final state is n = 3. What are the shortest and longest wavelengths (in nm) of Paschen spectral lines? Hints: The minimum value for ni is 4, the maximum value for ni is infinity and the Rydberg formula describes the emission spectra of hydrogen
Q11.13b
Spectral lines of Lyman and Balmer series do not overlap. Verify this statement.
S11.13b
A photon has a specific energy according to the energy between the excited and ground state.
E = (1/nf2 - 1/ni2), A = hv
The lyman series is when nf is the ground state or nf =1 and Balmer series is when nf =2
nf = 1 the value , ni from 2 to infinity with the values between 1 and ½. For the balmer series ni is from 3 to infinity the range between 1/4 and 5/36. Thus, these intervals don not overlap --> the energies do not overlap --> the lines in the series cant overlap
Q11.14
Assume the Rydberg constant for He+ is 9.72x10-18nm, calculate the wavelength of He+ ions from n=3 to n=2.
S11.14
\[\dfrac{1}{\lambda}=R_{H} \left | \dfrac{1}{n^{2}_{i}}-\dfrac{1}{n^{2}_{f}} \right | \nonumber \]
\[\dfrac{1}{\lambda}=9.72\times10^{-18} \left | \dfrac{1}{3^{2}}-\dfrac{1}{2^{2}} \right | \nonumber \]
\[\lambda=7.41\times10^{17}nm\nonumber \]
Q11.15
Derive from the following equation to solve for wavelength.
\(\Delta E=hcR_{H}(\dfrac{1}{n_{i}^{2}}-\dfrac{1}{n_{f}^{2}})\)
S11.15
\[\Delta E=R_{H} \left | \dfrac{1}{n^{2}_{i}}-\dfrac{1}{n^{2}_{f}} \right | \nonumber \]
\[\dfrac{v}{c}=\Delta E=R_{H} \left | \dfrac{1}{n^{2}_{i}}-\dfrac{1}{n^{2}_{f}} \right | \nonumber \]
\[\dfrac{1}{\lambda}=\dfrac{v}{c}=\Delta E=R_{H} \left | \dfrac{1}{n^{2}_{i}}-\dfrac{1}{n^{2}_{f}} \right | \nonumber \]
Q11.16
Photosynthesis occurs when light excites the electrons in the chloroplasts of leaves. If you flash a light of 500 nm at the plant and assuming your flashlight emits 4.5x1020 numbers of photons, how much energy in joules was that one flash?
Q11.50
What is an antiatom? How is it different from a regular hydrogen? What will happen if these two collided with one another?
S11.50
An antiatom is a hydrogen atom with reversed electrical charges compared to that of a hydrogen atom. The proton is called an antiproton and it bears a negative charge rather than a positive charge. The electron, or antielectron, has a positive charge rather than a negative charge. As a result, an antiatom and regular hydrogen would obliterate one another should they collide. Subsequent energy would then be released.
Q11.51
A scientist determined the kinetic energy released electrons of cesium metal through a photoelectric experiment. Determine h and the \work function for cesium graphically from the following results:
| λ/nm | 410 | 420 | 475 | 500 | 550 | 630 |
|---|---|---|---|---|---|---|
| V/volt | 1.6 | 1.4 | 1.1 | 0.91 | 0.72 |
0.37 |
S11.51
First, convert wavelength to frequency and volt to energy in J.
| f (1/sec) | Energy (J) |
|---|---|
| \(7.31707 \times 10^{15}\) | 1.6 |
| \(7.14286 \times 10^{15}\) | 1.4 |
| \(6.3157 \times 10^{15}\) | 1.1 |
| \(6 \times 10^{15}\) | 0.91 |
| \(5.45455 \times 10^{15}\) | 0.72 |
| \(4.7619 \times 10^{15}\) | 0.32 |
Then graph the values and determine the linear equation.
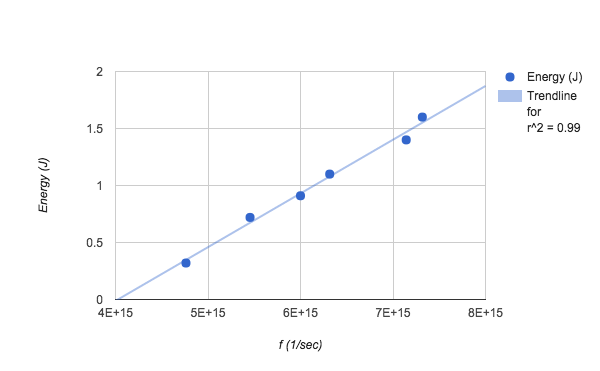
The linear equation is
\[y=4.7 \times 10^{-16} f - 1.89\nonumber \]
Use the equation below:
hf-=Ek (max kinetic energy)
h=slope
= y-intercept
h= 4.7 X 10-16
= 1.89
Q11.52
Calculate the de Broglie wavelength of a Cl2 molecule at 300 K.
S11.52
\[ v_{rms} = \sqrt{\dfrac{3RT}{M}}\nonumber \]
=((3)(8.314)(300)/(70.8X10-3 kg) = 325 m/s
\[ \lambda = \dfrac{h}{mv_{rms}}\nonumber \]
=(6.626X10-34 J*s)/[(70.8 amu)(1.66X10-27 kg/amu)(325 m/s)] = 1.73 X 10-11 m
Q11.53
Consider a balloon with a diameter of \(2.5 \times 10^{-5}\; m\). What is the uncertainty of the velocity of an oxygen molecule that is trapped inside.
S11.53
Use the direct application of the uncertainty principle:
\[ \Delta x \Delta p \ge \dfrac{h}{4 \pi}\nonumber \]
Let's consider the molecule has an uncertainly that is \(\pm\, radius\) of the balloon.
\[\Delta x = 1.3 \times 10^{-5}\; m\nonumber \]
The uncertainty of the momentum of the molecule can be estimated via the uncertainty principle.
\[ \Delta p =\dfrac{h}{4 \pi \Delta x} = \dfrac{(6.626 \times 10^{-34} J*s)}{(4\pi) (1.3 \times 10^{-5}\; m)} = 4.05 \times 10^{-30} kg\,m\,s^{-1}\nonumber \]
This can be converted to uncertainty in velocity via
\[p=mv\nonumber \]
or
\[ \Delta p =m_e \Delta v\nonumber \]
with the electron mass \(m_e\) equal to \(9.109 \times 10^{-31}\; kg\). since the mass of the molecule is not uncertain.
\[ \Delta v = \dfrac{ \Delta p }{ m_e } = \dfrac{4.05 \times 10^{-30}}{9.109 \times 10^{-31}\; kg} = 4.5\; m/s\nonumber \]
Q11.55
What conditions must be satisfied for the Schrodinger's equation for \(\psi\) to be an acceptable wavefunction. What are some examples of unacceptable wave functions?
Q11.56
The equation for calculating the energies of the electron in a hydrogen atom or a hydrogenlike ion is given by En = -(2.18 x10^-18 J)Z^2(1/n^2), where Z is the atomic number of the element. One way to modify this equation for many-electron atoms is to replace Z with (Z- [sigma]), where [sigma] is a positive dimensionless quantity called the shielding constant. Consider the lithium atom as an example. The physical significance of sigma that it represents the extent of shielding that the two 1s electrons exert on each other. Thus the quantity (Z - [sigma]) is appropriated called the "effective nuclear change." Use the first ionization energy of lithium to calculate the value of [sigma].
Q11.57
Calculate the wavelength and frequency of an emitted gamma particle that has energy of 3.11 x 10^12 J mol^-1.

