11.10: The Schrödinger Wave Equation for the Hydrogen Atom
- Page ID
- 41377
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The hydrogen atom, consisting of an electron and a proton, is a two-particle system, and the internal motion of two particles around their center of mass is equivalent to the motion of a single particle with a reduced mass. This reduced particle is located at \(r\), where \(r\) is the vector specifying the position of the electron relative to the position of the proton. The length of \(r\) is the distance between the proton and the electron, and the direction of \(r\) and the direction of \(r\) is given by the orientation of the vector pointing from the proton to the electron. Since the proton is much more massive than the electron, we will assume throughout this chapter that the reduced mass equals the electron mass and the proton is located at the center of mass.
Since the internal motion of any two-particle system can be represented by the motion of a single particle with a reduced mass, the description of the hydrogen atom has much in common with the description of a diatomic molecule discussed previously. The Schrödinger Equation for the hydrogen atom
\[ \hat {H} (r , \theta , \varphi ) \psi (r , \theta , \varphi ) = E \psi ( r , \theta , \varphi) \label {6.1.1}\]
employs the same kinetic energy operator, \(\hat {T}\), written in spherical coordinates. For the hydrogen atom, however, the distance, r, between the two particles can vary, unlike the diatomic molecule where the bond length was fixed, and the rigid rotor model was used. The hydrogen atom Hamiltonian also contains a potential energy term, \(\hat {V}\), to describe the attraction between the proton and the electron. This term is the Coulomb potential energy,
\[ \hat {V} (r) = - \dfrac {e^2}{4 \pi \epsilon _0 r } \label {6.1.2}\]
where \(r\) is the distance between the electron and the proton. The Coulomb potential energy depends inversely on the distance between the electron and the nucleus and does not depend on any angles. Such a potential is called a central potential.
It is convenient to switch from Cartesian coordinates \(x, y, z\) to spherical coordinates in terms of a radius \(r\), as well as angles \(\phi\), which is measured from the positive x axis in the xy plane and may be between 0 and \(2\pi\), and \(\theta\), which is measured from the positive z axis towards the xy plane and may be between 0 and \(\pi\).
The time-indepdent Schrödinger equation (in spherical coordinates) for a electron around a positively charged nucleus is then
\[ \left \{ -\dfrac {\hbar ^2}{2 \mu r^2} \left [ \dfrac {\partial}{\partial r} \left (r^2 \dfrac {\partial}{\partial r} \right ) + \dfrac {1}{\sin \theta } \dfrac {\partial}{\partial \theta } \left ( \sin \theta \dfrac {\partial}{\partial \theta} \right ) + \dfrac {1}{\sin ^2 \theta} \dfrac {\partial ^2}{\partial \varphi ^2} \right ] - \dfrac {e^2}{4 \pi \epsilon _0 r } \right \} \psi (r , \theta , \varphi ) = E \psi (r , \theta , \varphi ) \label {6.1.4}\]
Since the angular momentum operator does not involve the radial variable, \(r\), we can separate variables in Equation \(\ref{6.1.4}\) by using a product wavefunction. We know that the eigenfunctions of the angular momentum operator are the Spherical Harmonic functions (Table M4), \(Y (\theta , \varphi )\), so a good choice for a product function is
\[ \color{red} \psi (r , \theta , \varphi ) = R (r) Y (\theta , \varphi ) \label {6.1.8}\]
The Spherical Harmonic \(Y (\theta , \varphi )\) functions provide information about where the electron is around the proton, and the radial function \(R(r)\) describes how far the electron is away from the proton. A solution for both \(R(r)\) and \(Y (\theta , \varphi ) \) with \(E_n\) that depends on only one quantum number \(n\), although others are required for the proper description of the wavefunction:
\[ \color{red} E_n = -\dfrac {m_e e^4}{8\epsilon_0^2 h^2 n^2}\label{6}\]
with \(n=1,2,3 ...\infty\)
The hydrogen atom wavefunctions, \(\psi (r, \theta , \phi )\), are called atomic orbitals. An atomic orbital is a function that describes one electron in an atom. The wavefunction with n = 1, \(l\) \(l\) = 0 is called the 1s orbital, and an electron that is described by this function is said to be “in” the ls orbital, i.e. have a 1s orbital state. The constraints on n, \(l\) \(l)\), and \(m_l\) that are imposed during the solution of the hydrogen atom Schrödinger equation explain why there is a single 1s orbital, why there are three 2p orbitals, five 3d orbitals, etc. We will see when we consider multi-electron atoms, these constraints explain the features of the Periodic Table. In other words, the Periodic Table is a manifestation of the Schrödinger model and the physical constraints imposed to obtain the solutions to the Schrödinger equation for the hydrogen atom.
The Three Quantum Numbers
Schrödinger’s approach requires three quantum numbers (\(n\), \(l\), and \(m_l\)) to specify a wavefunction for the electron. The quantum numbers provide information about the spatial distribution of an electron. Although \(n\) can be any positive integer (NOT zero), only certain values of \(l\) and \(m_l\) are allowed for a given value of \(n).
The principal quantum number (n): One of three quantum numbers that tells the average relative distance of an electron from the nucleus. indicates the energy of the electron and the average distance of an electron from the nucleus
\[ n = 1,\;2,\;3,\;4,\;.\;.\;.\; \label{2.2.2} \]
As\( \)n increases for a given atom, so does the average distance of an electron from the nucleus. A negatively charged electron that is, on average, closer to the positively charged nucleus is attracted to the nucleus more strongly than an electron that is farther out in space. This means that electrons with higher values of n are easier to remove from an atom. All wave functions that have the same value of n are said to constitute a principal shell. All the wave functions that have the same value of n because those electrons have similar average distances from the nucleus. because those electrons have similar average distances from the nucleus. As you will see, the principal quantum number n corresponds to the n used by Bohr to describe electron orbits and by Rydberg to describe atomic energy levels.
The Azimuthal Quantum Number: The second quantum number is often called the azimuthal quantum number (l). One of three quantum numbers that describes the shape of the region of space occupied by an electron.. The value of l describes the shape of the region of space occupied by the electron. The allowed values of l depend on the value of n and can range from 0 to n − 1:
\[ l = 0,\;1,.,2,\;3,\;.\;.\;\left (n-1 \right ) \label{2.2.3} \]
For example, if n = 1, l can be only 0; if n = 2, l can be 0 or 1; and so forth. For a given atom, all wave functions that have the same values of both n and l form a subshell. A group of wave functions that have the same values of n and l. The regions of space occupied by electrons in the same subshell usually have the same shape, but they are oriented differently in space.
The Magnetic Quantum Number: The third quantum number is the magnetic quantum number (\(m_l\)). One of three quantum numbers that describes the orientation of the region of space occupied by an electron with respect to an applied magnetic field.. The value of \(m_l\) describes the orientation of the region in space occupied by an electron with respect to an applied magnetic field. The allowed values of \(m_l\) depend on the value of l: \(m_l\) can range from −l to l in integral steps:
\[ m = -l,\;-l+1,\,.\;.\;.0,\;\,.\;.\;.l-1,l \label{2.2.4} \]
For example, if \(l = 0\), ml can be only 0; if l = 1, \(m_l\) can be −1, 0, or +1; and if l = 2, \(m_l\) can be −2, −1, 0, +1, or +2.
Each wave function with an allowed combination of n, l, and ml values describes an atomic orbital A wave function with an allowed combination of n, l and ml quantum numbers., a particular spatial distribution for an electron. For a given set of quantum numbers, each principal shell has a fixed number of subshells, and each subshell has a fixed number of orbitals.
Example \(\PageIndex{1}\): Number of subshells
How many subshells and orbitals are contained within the principal shell with n = 4?
Given: value of n
Asked for: number of subshells and orbitals in the principal shell
Strategy:
A Given n = 4, calculate the allowed values of l. From these allowed values, count the number of subshells.
B For each allowed value of l, calculate the allowed values of ml. The sum of the number of orbitals in each subshell is the number of orbitals in the principal shell.
Solution
A We know that l can have all integral values from 0 to n − 1. If n = 4, then l can equal 0, 1, 2, or 3. Because the shell has four values of l, it has four subshells, each of which will contain a different number of orbitals, depending on the allowed values of ml.
B For l = 0, ml can be only 0, and thus the l = 0 subshell has only one orbital. For l = 1, ml can be 0 or ±1; thus the l = 1 subshell has three orbitals. For l = 2, ml can be 0, ±1, or ±2, so there are five orbitals in the l = 2 subshell. The last allowed value of l is l = 3, for which ml can be 0, ±1, ±2, or ±3, resulting in seven orbitals in the l = 3 subshell. The total number of orbitals in the n = 4 principal shell is the sum of the number of orbitals in each subshell and is equal to n2:
\( \mathop 1\limits_{(l = 0)} + \mathop 3\limits_{(l = 1)} + \mathop 5\limits_{(l = 2)} + \mathop 7\limits_{(l = 3)} = 16\; {\rm{orbitals}} = {(4\; {\rm{principal\: shells}})^2} \)
Exercise \(\PageIndex{1}\)
How many subshells and orbitals are in the principal shell with n = 3?
Answer: three subshells; nine orbitals
Rather than specifying all the values of n and l every time we refer to a subshell or an orbital, chemists use an abbreviated system with lowercase letters to denote the value of l for a particular subshell or orbital:
| l = | 0 | 1 | 2 | 3 |
| Designation | s | p | d | f |
The principal quantum number is named first, followed by the letter s, p, d, or f as appropriate. These orbital designations are derived from corresponding spectroscopic characteristics of lines involving them: sharp, principle, diffuse, and fundamental. A 1s orbital has n = 1 and l = 0; a 2p subshell has n = 2 and l = 1 (and has three 2p orbitals, corresponding to ml = −1, 0, and +1); a 3d subshell has n = 3 and l = 2 (and has five 3d orbitals, corresponding to ml = −2, −1, 0, +1, and +2); and so forth.
We can summarize the relationships between the quantum numbers and the number of subshells and orbitals as follows (Table \(\PageIndex{1}\)):
- Each principal shell has n subshells. For n = 1, only a single subshell is possible (1s); for n = 2, there are two subshells (2s and 2p); for n = 3, there are three subshells (3s, 3p, and 3d); and so forth. Every shell has an ns subshell, any shell with n ≥ 2 also has an np subshell, and any shell with n ≥ 3 also has an nd subshell. Because a 2d subshell would require both n = 2 and l = 2, which is not an allowed value of l for n = 2, a 2d subshell does not exist.
- Each subshell has 2l + 1 orbitals. This means that all ns subshells contain a single s orbital, all np subshells contain three p orbitals, all nd subshells contain five d orbitals, and all nf subshells contain seven f orbitals.
Note
Each principal shell has n subshells, and each subshell has 2l + 1 orbitals.
| n | l | Subshell Designation | ml | Number of Orbitals in Subshell | Number of Orbitals in Shell |
|---|---|---|---|---|---|
| 1 | 0 | 1s | 0 | 1 | 1 |
| 2 | 0 | 2s | 0 | 1 | 4 |
| 1 | 2p | −1, 0, 1 | 3 | ||
| 3 | 0 | 3s | 0 | 1 | 9 |
| 1 | 3p | −1, 0, 1 | 3 | ||
| 2 | 3d | −2, −1, 0, 1, 2 | 5 | ||
| 4 | 0 | 4s | 0 | 1 | 16 |
| 1 | 4p | −1, 0, 1 | 3 | ||
| 2 | 4d | −2, −1, 0, 1, 2 | 5 | ||
| 3 | 4f | −3, −2, −1, 0, 1, 2, 3 | 7 |
The Radial Component
The first six radial functions are provided in Table \(\PageIndex{2}\). Note that the functions in the table exhibit a dependence on \(Z\), the atomic number of the nucleus. Other one electron systems have electronic states analogous to those for the hydrogen atom, and inclusion of the charge on the nucleus allows the same wavefunctions to be used for all one-electron systems. For hydrogen, \(Z = 1\) and for helium, \(Z=2\).
| \(n\) |
\(\ell\) |
\(m\) | Radial Component |
|---|---|---|---|
| \(n=1\) | \(\ell=0\) | \(m=0\) | \(\psi_{100} = \dfrac {1}{\sqrt {\pi}} \left(\dfrac {Z}{a_0}\right)^{\frac {3}{2}} e^{-\rho}\) |
| \(n=2\) | \(\ell=0\) | \(m=0\) | \(\psi_{200} = \dfrac {1}{\sqrt {32\pi}} \left(\dfrac {Z}{a_0}\right)^{\frac {3}{2}} (2-\rho)e^{\dfrac {-\rho}{2}}\) |
| \(\ell=1\) | \(m=0\) | \(\psi_{210} = \dfrac {1}{\sqrt {32\pi}} \left(\dfrac {Z}{a_0}\right)^{\frac {3}{2}} \rho e^{-\rho/2} \cos(\theta)\) | |
| \(\ell=1\) | \(m=\pm 1\) | \(\psi_{21\pm\ 1} = \dfrac {1}{\sqrt {64\pi}} \left(\dfrac {Z}{a_0}\right)^{\dfrac {3}{2}} \rho e^{-\rho/2} \sin(\theta) e^{\pm\ i\phi}\) | |
| \(n=3\) | \(\ell=0\) | \(m=0\) | \(\psi_{300} = \dfrac {1}{81\sqrt {3\pi}} \left(\dfrac {Z}{a_0}\right)^{\frac {3}{2}} (27-18\rho +2\rho^2)e^{-\rho/3}\) |
| \(\ell=1\) | \(m=0\) | \(\psi_{310} = \dfrac{1}{81} \sqrt {\dfrac {2}{\pi}} \left(\dfrac {Z}{a_0}\right)^{\dfrac {3}{2}} (6r - \rho^2)e^{-\rho/3} \cos(\theta)\) | |
| \(\ell=1\) | \(m=\pm 1\) | \(\psi_{31\pm\ 1} = \dfrac {1}{81\sqrt {\pi}} \left(\dfrac {Z}{a_0}\right)^{\frac {3}{2}} (6\rho - \rho^2)e^{-r/3} \sin(\theta)e^{\pm\ i \phi}\) | |
| \(\ell=2\) | \(m=0\) | \(\psi_{320} = \dfrac {1}{81\sqrt {6\pi}} \left(\dfrac {Z}{a_0}\right)^{\frac {3}{2}} \rho^2 e^{-\rho/3}(3cos^2(\theta) -1)\) | |
| \(\ell=2\) | \(m=\pm 1\) | \(\psi_{32\pm\ 1} = \dfrac {1}{81\sqrt {\pi}} \left(\dfrac {Z}{a_0}\right)^{\frac {3}{2}} \rho^2 e^{-\rho/3} \sin(\theta)\cos(\theta)e^{\pm\ i \phi}\) | |
| \(\ell=2\) | \(m=\pm 2\) |
\(\psi_{32\pm\ 2} = \dfrac {1}{162\sqrt {\pi}} \left(\dfrac {Z}{a_0}\right)^{\frac {3}{2}} \rho^2 e^{-\rho/3}{\sin}^2(\theta)e^{\pm\ 2i\phi}\) |
Visualizing the variation of an electronic wavefunction with r,\(\theta\), and \(\phi\) is important because the absolute square of the wavefunction depicts the charge distribution (electron probability density) in an atom or molecule. The charge distribution is central to chemistry because it is related to chemical reactivity. For example, an electron deficient part of one molecule is attracted to an electron rich region of another molecule, and such interactions play a major role in chemical interactions ranging from substitution and addition reactions to protein folding and the interaction of substrates with enzymes.
Methods for separately examining the radial portions of atomic orbitals provide useful information about the distribution of charge density within the orbitals. Graphs of the radial functions, R(r), for the 1s, 2s, and 2p orbitals plotted in Figure \(\PageIndex{2}\) left). The quantity \(R(r)^* R(r)\) gives the radial probability density; i.e., the probability density for the electron to be at a point located the distance r from the proton. Radial probability densities for three types of atomic orbitals are plotted in Figure \(\PageIndex{2}\) (right).

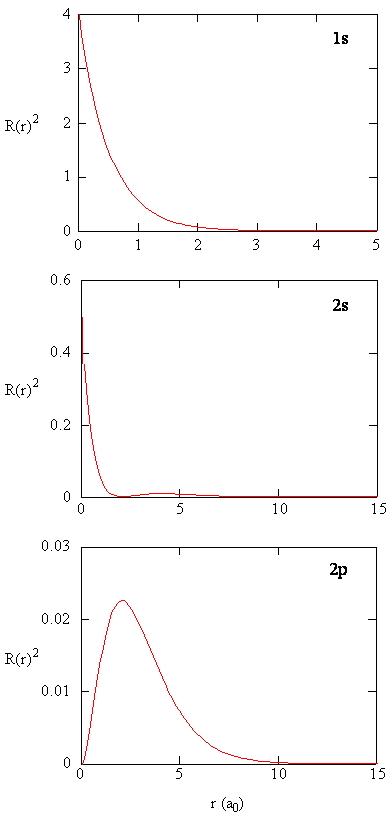
For the hydrogen atom, the peak in the radial probability plot occurs at r = 0.529 Å (52.9 pm), which is exactly the radius calculated by Bohr for the n = 1 orbit. Thus the most probable radius obtained from quantum mechanics is identical to the radius calculated by classical mechanics. In Bohr’s model, however, the electron was assumed to be at this distance 100% of the time, whereas in the Schrödinger model, it is at this distance only some of the time. The difference between the two models is attributable to the wavelike behavior of the electron and the Heisenberg uncertainty principle.
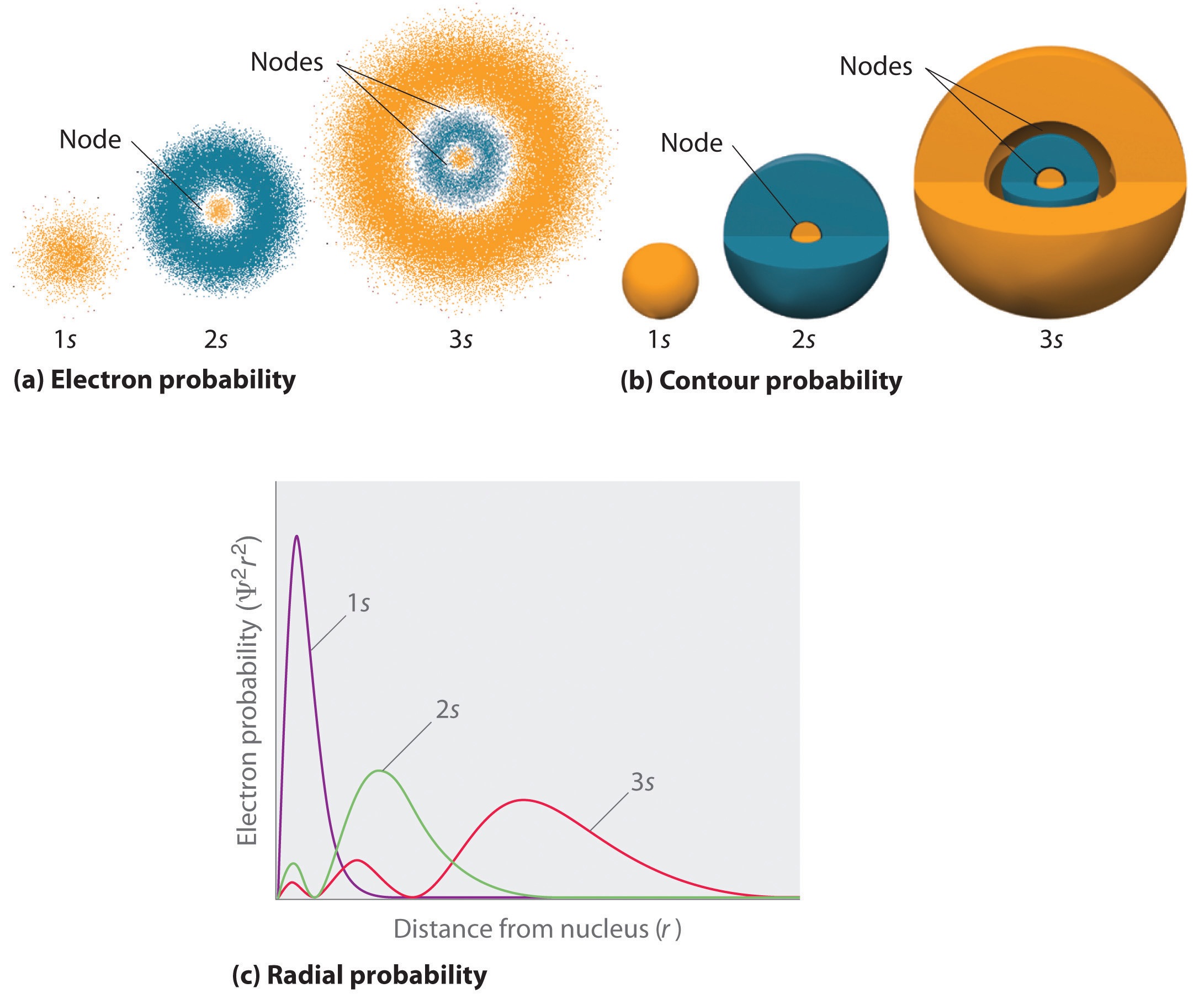
Figure \(\PageIndex{3}\) compares the electron probability densities for the hydrogen 1s, 2s, and 3s orbitals. Note that all three are spherically symmetrical. For the 2s and 3s orbitals, however (and for all other s orbitals as well), the electron probability density does not fall off smoothly with increasing r. Instead, a series of minima and maxima are observed in the radial probability plots (part (c) in Figure \(\PageIndex{3}\)). The minima correspond to spherical nodes (regions of zero electron probability), which alternate with spherical regions of nonzero electron probability.
The Angular Component
The angular component of the wavefunction \(Y(\theta,\phi)\) in Equation \(\ref{6.1.8}\) does much to give an orbital its distinctive shape. \(Y(\theta,\phi)\) is typically normalized so the the integral of \(Y^2(\theta,\phi)\) over the unit sphere is equal to one. In this case, \(Y^2(\theta,\phi)\) serves as a probability function. The probability function can be interpreted as the probability that the electron will be found on the ray emitting from the origin that is at angles \((\theta,\phi)\) from the axes. The probability function can also be interpreted as the probability distribution of the electron being at position \((\theta,\phi)\) on a sphere of radius r, given that it is r distance from the nucleus. \(Y_{l,m_l}(\theta,\phi)\) are also the wavefunction solutions to Schrödinger’s equation for a rigid rotor consisting of rotating bodies, for example a diatomic molecule. These are called Spherical Harmonic functions (Table M4).
s Orbitals (l=0)
Three things happen to s orbitals as n increases (Figure 6.6.2):
- They become larger, extending farther from the nucleus.
- They contain more nodes. This is similar to a standing wave that has regions of significant amplitude separated by nodes, points with zero amplitude.
- For a given atom, the s orbitals also become higher in energy as n increases because of their increased distance from the nucleus.
Orbitals are generally drawn as three-dimensional surfaces that enclose 90% of the electron density. Although such drawings show the relative sizes of the orbitals, they do not normally show the spherical nodes in the 2s and 3s orbitals because the spherical nodes lie inside the 90% surface. Fortunately, the positions of the spherical nodes are not important for chemical bonding.
p Orbitals (l=1)
Only s orbitals are spherically symmetrical. As the value of l increases, the number of orbitals in a given subshell increases, and the shapes of the orbitals become more complex. Because the 2p subshell has l = 1, with three values of ml (−1, 0, and +1), there are three 2p orbitals).

The electron probability distribution for one of the hydrogen 2p orbitals is shown in Figure \(\PageIndex{4}\). Because this orbital has two lobes of electron density arranged along the z axis, with an electron density of zero in the xy plane (i.e., the xy plane is a nodal plane), it is a 2pz orbital. As shown in Figure \(\PageIndex{5}\), the other two 2p orbitals have identical shapes, but they lie along the x axis (2px) and y axis (2py), respectively. Note that each p orbital has just one nodal plane. In each case, the phase of the wave function for each of the 2p orbitals is positive for the lobe that points along the positive axis and negative for the lobe that points along the negative axis. It is important to emphasize that these signs correspond to the phase of the wave that describes the electron motion, not to positive or negative charges.
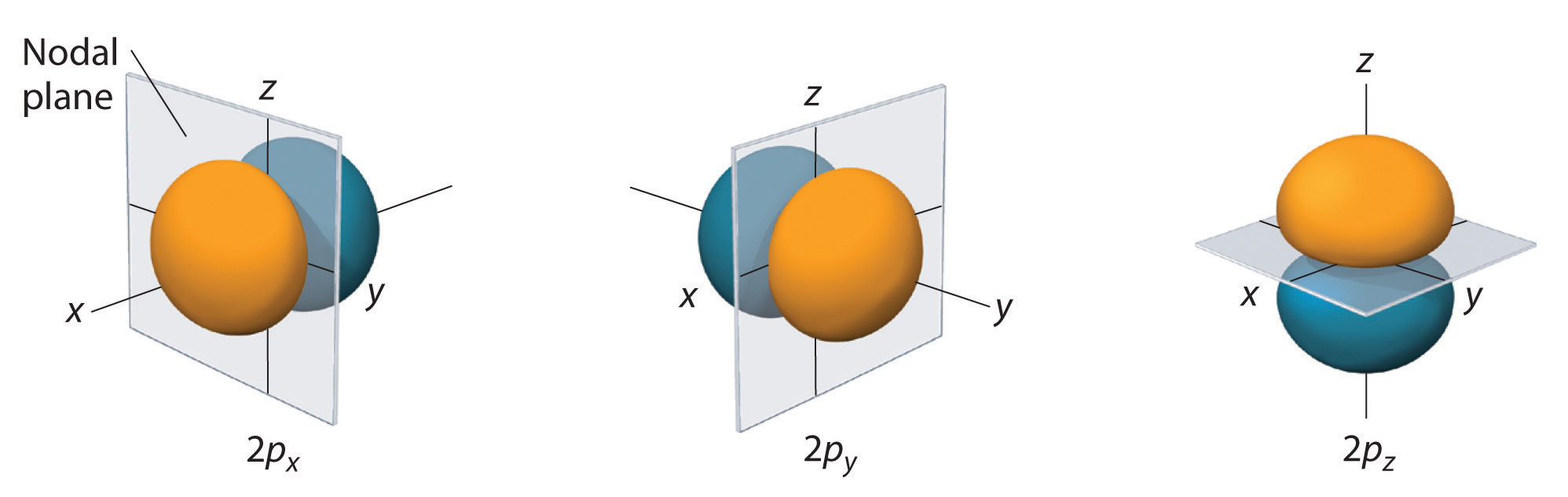
The surfaces shown enclose 90% of the total electron probability for the 2px, 2py, and 2pz orbitals. Each orbital is oriented along the axis indicated by the subscript and a nodal plane that is perpendicular to that axis bisects each 2p orbital. The phase of the wave function is positive (orange) in the region of space where x, y, or z is positive and negative (blue) where x, y, or z is negative. Just as with the s orbitals, the size and complexity of the p orbitals for any atom increase as the principal quantum number n increases. The shapes of the 90% probability surfaces of the 3p, 4p, and higher-energy p orbitals are, however, essentially the same as those shown in Figure Figure \(\PageIndex{5}\).
d Orbitals (l=2)
Subshells with l = 2 have five d orbitals; the first principal shell to have a d subshell corresponds to n = 3. The five d orbitals have ml values of −2, −1, 0, +1, and +2 (Figure \(\PageIndex{6}\)).
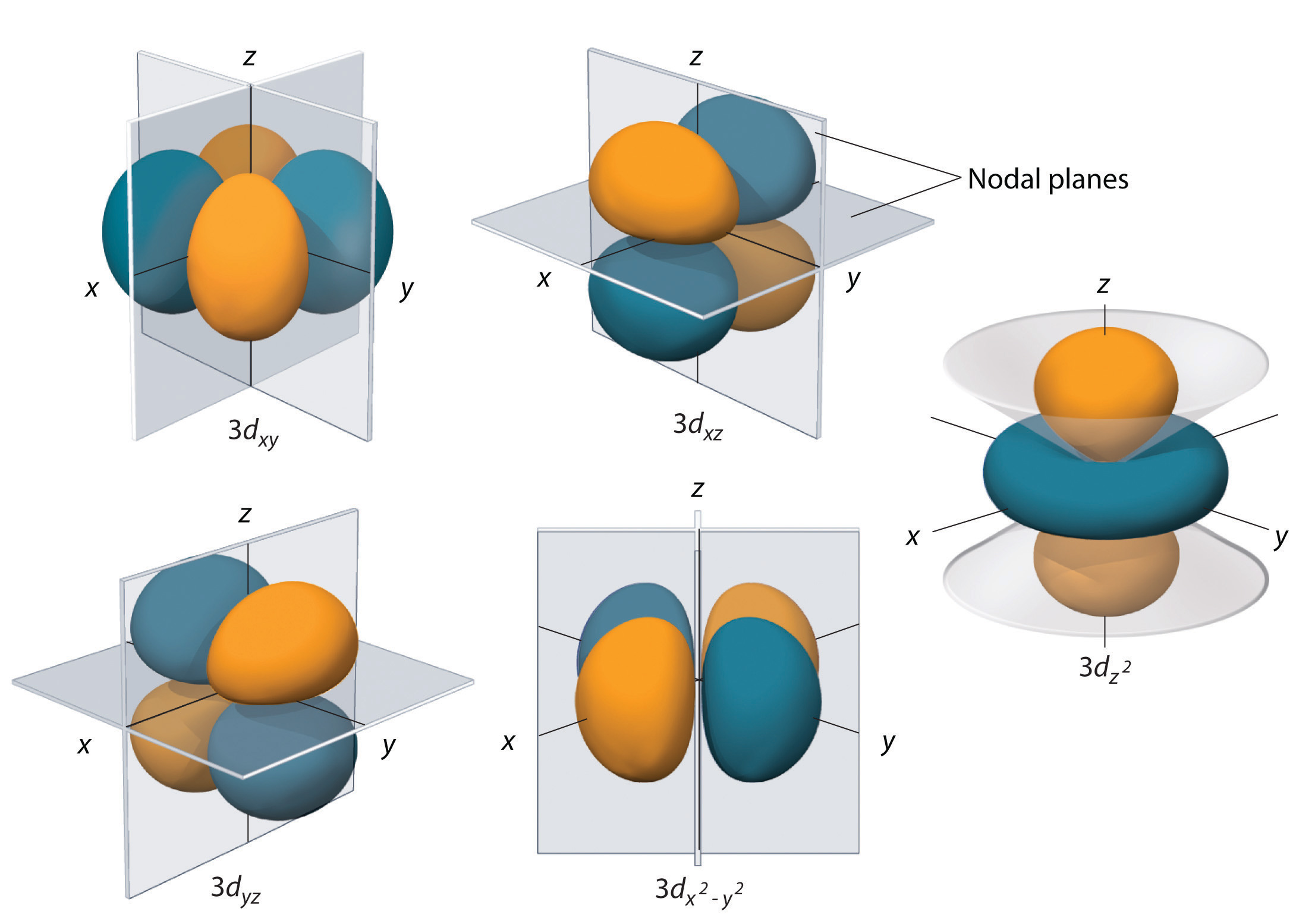
The hydrogen 3d orbitals have more complex shapes than the 2p orbitals. All five 3d orbitals contain two nodal surfaces, as compared to one for each p orbital and zero for each s orbital. In three of the d orbitals, the lobes of electron density are oriented between the x and y, x and z, and y and z planes; these orbitals are referred to as the \(3d_{xy}\), \)3d_{xz}\_, and \)3d_{yz}\) orbitals, respectively. A fourth d orbital has lobes lying along the x and y axes; this is the 3dx2−y2 orbital. The fifth 3d orbital, called the \(3d_{z^2}\) orbital, has a unique shape: it looks like a \(2p_z\) orbital combined with an additional doughnut of electron probability lying in the xy plane. Despite its peculiar shape, the \(3d_{z^2}\) orbital is mathematically equivalent to the other four and has the same energy. In contrast to p orbitals, the phase of the wave function for d orbitals is the same for opposite pairs of lobes. As shown in Figure \(\PageIndex{6}\), the phase of the wave function is positive for the two lobes of the \(dz^2\) orbital that lie along the z axis, whereas the phase of the wave function is negative for the doughnut of electron density in the xy plane. Like the s and p orbitals, as n increases, the size of the d orbitals increases, but the overall shapes remain similar to those depicted in Figure 6.6.5.
f Orbitals (l=3)
Principal shells with n = 4 can have subshells with l = 3 and ml values of −3, −2, −1, 0, +1, +2, and +3. These subshells consist of seven f orbitals. Each f orbital has three nodal surfaces, so their shapes are complex (not shown).
Energies
The constraint that \(n\) be greater than or equal to \(l +1\) also turns out to quantize the energy, producing the same quantized expression for hydrogen atom energy levels that was obtained from the Bohr model of the hydrogen atom.
\[E=−\dfrac{Z^2}{n^2}Rhc \label{6.6.1}\]
or
\[ E_n = - \dfrac {Z^2 \mu e^4}{8 \epsilon ^2_0 h^2 n^2} \]
The relative energies of the atomic orbitals with n ≤ 4 for a hydrogen atom are plotted in Figure \(\PageIndex{7}\) ; note that the orbital energies depend on only the principal quantum number n. Consequently, the energies of the 2s and 2p orbitals of hydrogen are the same; the energies of the 3s, 3p, and 3d orbitals are the same; and so forth. The orbital energies obtained for hydrogen using quantum mechanics are exactly the same as the allowed energies calculated by Bohr. In contrast to Bohr’s model, however, which allowed only one orbit for each energy level, quantum mechanics predicts that there are 4 orbitals with different electron density distributions in the n = 2 principal shell (one 2s and three 2p orbitals), 9 in the n = 3 principal shell, and 16 in the n = 4 principal shell.
Note
For a single electron system, the energy of that electron is a function of only the principal quantum number (Equation \(\ref{6.6.1}\)).
The different values of l and ml for the individual orbitals within a given principal shell are not important for understanding the emission or absorption spectra of the hydrogen atom under most conditions, but they do explain the splittings of the main lines that are observed when hydrogen atoms are placed in a magnetic field. As we have just seen, however, quantum mechanics also predicts that in the hydrogen atom, all orbitals with the same value of n (e.g., the three 2p orbitals) are degenerate, meaning that they have the same energy. Figure \(\PageIndex{7}\) shows that the energy levels become closer and closer together as the value of n increases, as expected because of the 1/n2 dependence of orbital energies.
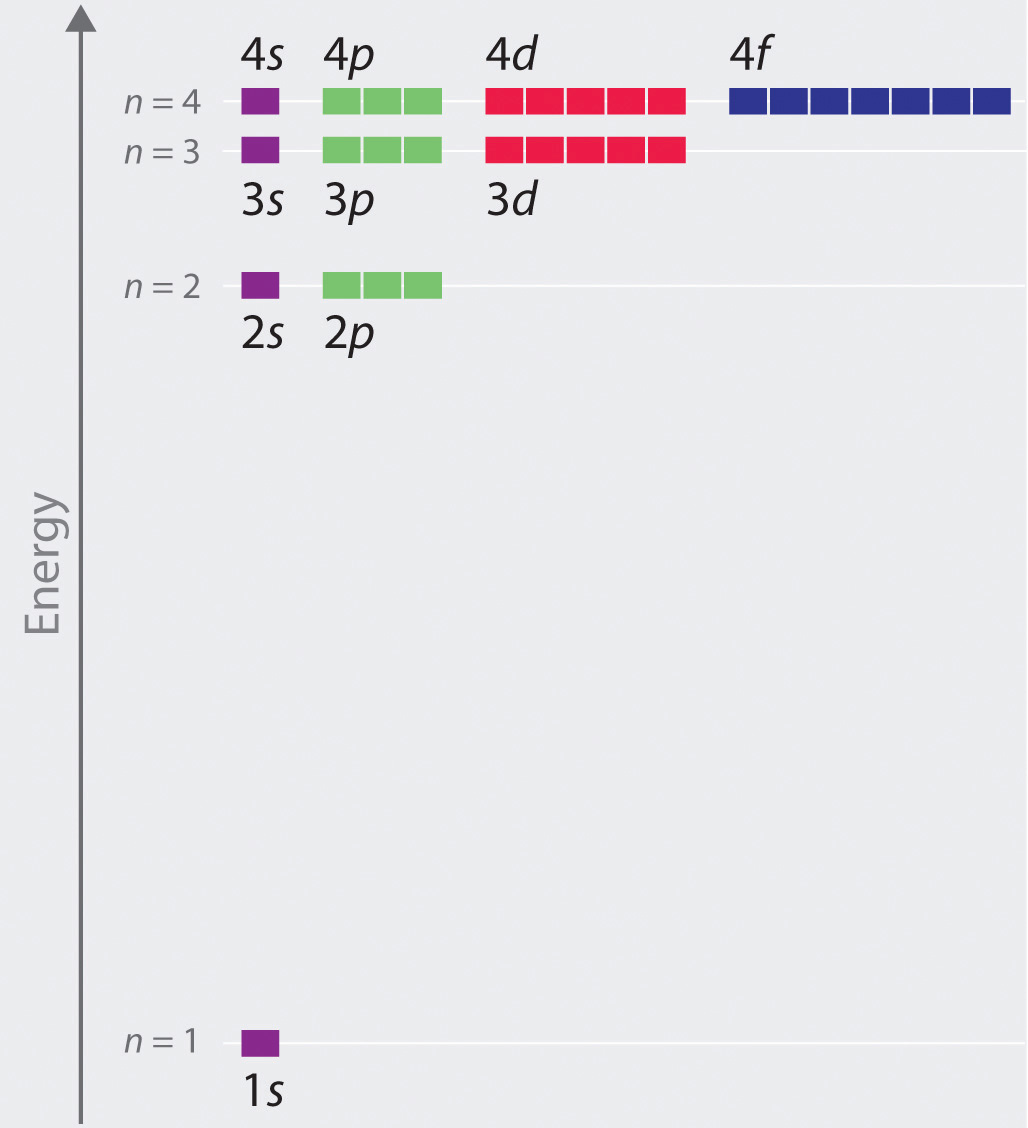
In general, both energy and radius decrease as the nuclear charge increases. Thus the most stable orbitals (those with the lowest energy) are those closest to the nucleus. For example, in the ground state of the hydrogen atom, the single electron is in the 1s orbital, whereas in the first excited state, the atom has absorbed energy and the electron has been promoted to one of the n = 2 orbitals. In ions with only a single electron, the energy of a given orbital depends on only n, and all subshells within a principal shell, such as the px, py, and pz orbitals, are degenerate.
Note: Bohr vs. Schrödinger
It is interesting to compare the results obtained by solving the Schrödinger equation with Bohr’s model of the hydrogen atom. There are several ways in which the Schrödinger model and Bohr model differ.
- First, and perhaps most strikingly, the Schrödinger model does not produce well-defined orbits for the electron. The wavefunctions only give us the probability for the electron to be at various directions and distances from the proton.
- Second, the quantization of angular momentum is different from that proposed by Bohr. Bohr proposed that the angular momentum is quantized in integer units of \(\hbar\), while the Schrödinger model leads to an angular momentum of \((l (l +1) \hbar ^2)^{\dfrac {1}{2}}\).
- Third, the quantum numbers appear naturally during solution of the Schrödinger equation while Bohr had to postulate the existence of quantized energy states. Although more complex, the Schrödinger model leads to a better correspondence between theory and experiment over a range of applications that was not possible for the Bohr model.
Electron Spin: The Fourth Quantum Number
The quantum numbers \(n, \ l, \ m\) are not sufficient to fully characterize the physical state of the electrons in an atom. In 1926, Otto Stern and Walther Gerlach carried out an experiment that could not be explained in terms of the three quantum numbers \(n, \ l, \ m\) and showed that there is, in fact, another quantum-mechanical degree of freedom that needs to be included in the theory. The experiment is illustrated in the Figure \(\PageIndex{8}\). A beam of atoms (e.g. hydrogen or silver atoms) is sent through a spatially inhomogeneous magnetic field with a definite field gradient toward one of the poles. It is observed that the beam splits into two beams as it passes through the field region.
The fact that the beam splits into 2 beams suggests that the electrons in the atoms have a degree of freedom capable of coupling to the magnetic field. That is, an electron has an intrinsic magnetic moment \(M\) arising from a degree of freedom that has no classical analog. The magnetic moment must take on only 2 values according to the Stern-Gerlach experiment. The intrinsic property that gives rise to the magnetic moment must have some analog to a spin, \(S\); unlike position and momentum, which have clear classical analogs, spin does not. The implication of the Stern-Gerlach experiment is that we need to include a fourth quantum number, \(m_s\) in our description of the physical state of the electron. That is, in addition to give its principle, angular, and magnetic quantum numbers, we also need to say if it is a spin-up electron or a spin-down electron.
Note: Spin is a Quantum Phenomenon
Unlike position and momentum, which have clear classical analogs, spin does not.
George Uhlenbeck (1900–1988) and Samuel Goudsmit (1902–1978), proposed that the splittings were caused by an electron spinning about its axis, much as Earth spins about its axis. When an electrically charged object spins, it produces a magnetic moment parallel to the axis of rotation, making it behave like a magnet. Although the electron cannot be viewed solely as a particle, spinning or otherwise, it is indisputable that it does have a magnetic moment. This magnetic moment is called electron spin.

In an external magnetic field, the electron has two possible orientations (Figure \(\PageIndex{9}\)). These are described by a fourth quantum number (ms), which for any electron can have only two possible values, designated +½ (up) and −½ (down) to indicate that the two orientations are opposites; the subscript s is for spin. An electron behaves like a magnet that has one of two possible orientations, aligned either with the magnetic field or against it. The implications of electron spin for chemistry were recognized almost immediately by an Austrian physicist, Wolfgang Pauli (1900–1958; Nobel Prize in Physics, 1945), who determined that each orbital can contain no more than two electrons whoe developed the Pauli exclusion principle.
Note: Pauli Exclusion Principle
No two electrons in an atom can have the same values of all four quantum numbers (\(n\), \(l\), \(m_l\), \(m_s\)).
By giving the values of n, l, and ml, we also specify a particular orbital (e.g., 1s with n = 1, l = 0, ml = 0). Because ms has only two possible values (+½ or −½), two electrons, and only two electrons, can occupy any given orbital, one with spin up and one with spin down. With this information, we can proceed to construct the entire periodic table, which was originally based on the physical and chemical properties of the known elements.
Example \(\PageIndex{2}\)
List all the allowed combinations of the four quantum numbers (n, l, ml, ms) for electrons in a 2p orbital and predict the maximum number of electrons the 2p subshell can accommodate.
Given: orbital
Asked for: allowed quantum numbers and maximum number of electrons in orbital
Strategy:
- List the quantum numbers (n, l, ml) that correspond to an n = 2p orbital. List all allowed combinations of (n, l, ml).
- Build on these combinations to list all the allowed combinations of (n, l, ml, ms).
- Add together the number of combinations to predict the maximum number of electrons the 2p subshell can accommodate.
Solution:
A For a 2p orbital, we know that n = 2, l = n − 1 = 1, and ml = −l, (−l +1),…, (l − 1), l. There are only three possible combinations of (n, l, ml): (2, 1, 1), (2, 1, 0), and (2, 1, −1).
B Because ms is independent of the other quantum numbers and can have values of only +½ and −½, there are six possible combinations of (n, l, ml, ms): (2, 1, 1, +½), (2, 1, 1, −½), (2, 1, 0, +½), (2, 1, 0, −½), (2, 1, −1, +½), and (2, 1, −1, −½).
C Hence the 2p subshell, which consists of three 2p orbitals (2px, 2py, and 2pz), can contain a total of six electrons, two in each orbital.
Exercise \(\PageIndex{2}\)
List all the allowed combinations of the four quantum numbers (n, l, ml, ms) for a 6s orbital, and predict the total number of electrons it can contain.
Answer: (6, 0, 0, +½), (6, 0, 0, −½); two electrons
Contributors and Attributions
David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski ("Quantum States of Atoms and Molecules")

