5.E: Solutions (Exercises)
- Page ID
- 41331
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)5.5: Real Solutions
Q5.6
Calculate the molality for a 0.005M NH4SO4. What is the difference between the molarity and molality of the solution?
Q5.6
What is the difference between the molarity and the molality of a solution? Calculate the molality for a 0.05M ammonium sulfite [NH4SO3] solution.
S5.6
The molarity of a solution is the ratio between the number of moles of solute and the solution.
The molality of a solution is the ratio between the number of moles of solute and the mass of solvent:
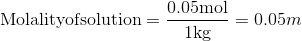
Q5.7
After taking tylenol for stomach pains, a man has 0.300 mg of acetaminophen in his 5.0 L blood. After 4 hours, there is 0.010 mg left in his blood. Calculate the number of moles of acetaminophen per ml of blood and the total number of moles and grams before and after. (Molar Mass of Acetaminophen: 151.2 g/mol)
S5.7
Before:
\(n=.300\times 10^{-3}g \times \dfrac{1mol}{151.2g}=1.98 \times 10^{-6}mol\)
\(M=\dfrac{1.98\times10^{-6}mol}{5.0L}(\dfrac{1000ml}{1L})=3.96\times 10^{-4}\dfrac{mol}{ml}\)
After:
\(n=.010\times 10^{-3}g \times \dfrac{1mol}{151.2g}=6.61 \times 10^{-8}mol\)
\(M=\dfrac{6.61\times10^{-8}mol}{5.0L}(\dfrac{1000ml}{1L})=1.32\times 10^{-5}\dfrac{mol}{ml}\)
Q5.16
If a diver swims to 50 ft below sea level, did the oxygen in his blood increase or decrease? What about a hiker who is 50 ft above sea level?
Q5.16
Charlie goes on a submarine ride with his family. On their submarine ride, they have dinner which Charlie washes down with a Coke. Charlie notes that upon the removal of the cap from the Coke bottle, it does not make much of a noise that he has grown accustomed to hearing when opening a soft drink bottle. Soon after their dinner, Charlie and his family make their way back up to the surface to disembark from their submarine journey. As they were ascending, Charlie started to burp. What has just occurred?
S5.16
When on a submarine, you submerge into the water and are below sea level. When below sea level, the total and partial pressures of CO2 increases in comparison to when you are at or above sea level. Since Charlie's family has brought the Coke down from land (at sea level), the solubility of the CO2 is increased and the concentration of the CO2 in solution is raised. When Charlie returns to sea level, the conditions go back to normal which causes both the pressure and the solubility to decrease and the CO2 inside of Charlie comes out and causes him to burp in order to release the CO2 gas.
Q5.17
Calculate the Henry's Law constant for O2 in blood at a partial pressure of 0.25. There's about 2.5 kg of blood in the individual and 15 g of \(O_2\) present.
S5.17
\[P_{O_2}=k\cdot m \rightarrow k=\dfrac{P_{0_2}}{m}\]
\(k=\dfrac{.25}{.188\dfrac{mol}{kg}}\)
\(M=(15.0g)(\dfrac{1mol}{32.0g})\)
Q5.18
Imagine the ideal gas \(F_2\) (at 25°C) has a solubility of \(123 \times 10^{-4}\; mol/L\) at a partial pressure of 0.5 atm, and \(321 \times 10^{-4}\) at 5 atm. Use Henry’s law to determine the number of moles of \(F_2\) at the given pressures.
Q5.19
Write the equation showing the relationship between the molality and the change of temperature. Show possible reasons that leading to the derivation of this equation.
S5.19
\[ \Delta T = K_b \times m_2\]
Molality is independent of temperature.
Q5.20
There are two liquids X and Y. The boiling point of liquid X is 125ºC while the boiling point of liquid Y is 250ºC. If liquids X and Y were mixed to form an ideal solution, would the boiling point of the solution be less than, greater than, or equal to that of (a) liquid X? (b) liquid Y?
S5.20
- Boiling point of solution > Boiling point of liquid X
- Boiling point of solution < Boiling point of liquid Y
Q5.25
Why don't you keep your honey in the fridge? Explain using the terms hypertonic, and hypotonic.
S5.25
Honey is a hypertonic solution and bacteria prefer a hypotonic environment.
Q5.27
The freezing point depression measurement of Compound X in Reagent A yields a molar mass of 144 g; the same measurement in Reagent Y gives a value of 72 g. What is the reason for this discrepancy? (Hint: Consider solvent-solute interactions).
Q5.28
What would be the volume of 20 moles of sugar (C12H22O11) dissolved in 0.5 g/cm^-3 of water at 10K? Given the freezing point depression constant for water is 1.86 K/mol kg, what would be the molality of the sugar?
Q5.28
You have a boiling pot with 4 L of water. You add 1000 grams of NaCl. Water boils at 100 o C and freezes at 0 o C. To what temperature is the boiling point of water elevated to with the addition of NaCl? To what temperature is the freezing point depressed to?
Q5.29a
Blood plasma, an enriched with platelets, contains several growth factors that help healing of tissues and bones. There are a lot of medical treatments which inject the comparable concentration of a certain solution into human blood. Explain why ?
S5.29a
The injected solution should be comparable to that of blood plasma. There is a certain amount of platelets which keep the state the blood plasma in equilibrium. If we inject too much, it significantly affects to human blood by changing the concentration of platelets.
Q5.29b
Immerse a human cell in hypertonic or hypotonic solution can cause harmful consequences. Explain what would happen in each situation and the case when we got injected with a high concentrated solutions in our vein?
Q5.30
The Davis water tower is 250 ft tall (about 76 meters). What is the osmotic pressure required to push water from the ground to the top of the tower?
S5.30
\[\pi = h\rho g\]
\[\pi = (76m)(1000kg \ m^{-3})(9.81 m \ s^{-2})\]
\[\pi = (7.456\ast 10^{5}N \ m^{-2})(\dfrac{1 atm}{1.013 \ast 10^{5}N\ m^{-2}})\]
\[\pi = 7.36 atm\]
Q5.31
A solution of liquid A is mixed with liquid B and exerts ideal behavior. At \(103^oC\) the total vapor pressure of a solution is 413mmHg containing 1.4 moles of A and 2.0 moles of B. After you add another mole of A to the solution, the vapor pressure increases to 486mmHg. At \(103^oC\) calculate the vapor pressure of pure A and B.
S5.31
Step1: (Hint: Calculate the mole fraction of A and B)
\[x_A=(\dfrac{molesA}{(molesA+molesB)})=(\dfrac{1.4molesA}{(1.4molesA+2.0molesB)})=.42\]
\[x_B=(\dfrac{molesB}{(molesA+molesB)})=(\dfrac{2.0molesB}{(1.4molesA+2.0molesB)})=.58\]
Step 2: (Hint: Set up total pressure equation)
\[P=x_AP^*_A+x_BP^*_B\]
\[413=(.42)P^*_A+(.58)P^*_B\]
Step 3: (Hint: Calculate the mole fraction of A and B with the addition of 1 mole of A)
\[x_A=(\dfrac{molesA}{(molesA+molesB)})=(\dfrac{2.4molesA}{(2.4molesA+2.0molesB)})=.55\]
\[x_B=(\dfrac{molesB}{(molesA+molesB)})=(\dfrac{2.0molesB}{(2.4molesA+2.0molesB)})=.45\]
Step 4: (Hint: Set up the second total pressure equation)
\[486=(.55)P^*_A+(.45)P^*_B\]
Step 5: (Hint: Solve for \(P^*_A\) and \(P^*_B\) by substitution of the two total pressure equations)
\[413=(.42)P^*_A+(.58)P^*_B\]
\[486=(.55)P^*_A+(.45)P^*_B\]
Rearrange equation 1
\[P^*_A=983.33-1.38095P^*_B\]
Substitute into any equation and solve for \(P^*_B\)
\[486=(.55)(983.33-1.38095P^*_B)+(.45)P^*_B\]
\[P^*_B=177.149mmHg\]
Substitute \(P^*_B\) into any equation to get \(P^*_A\)
\[P^*_A=983.33-1.38095P^*_B\]
\[=738.696mmHg\]
Q5.33
An ideal solution is composed of equal amount of component A with molar mass of 28.05g/mol and component B with molar mass of 80.91g/mol. At 35°C, component A has a vapor pressure of 0.2 atm and component B has a vapor pressure of 0.65 atm.
- Calculate the mole fraction of each component in the solution
- Calculate the partial pressure of each component at 35°C
- If some of the vapor condenses back into a liquid, what will the mole fraction of each component in this liquid and the vapor pressure above this liquid be?
S5.33
(a) remember mole fraction = (mole of solute) / (total mole of solution) ; \[n_A=\dfrac{weight_A}{28.05g/mol}\\
n_B=\dfrac{weight_B}{80.91g/mol}\\x_A=\dfrac{n_A}{n_A+n_B}=\dfrac{\dfrac{weight_A}{28.05g/mol}}{\dfrac{weight_A}{28.05g/mol}+\dfrac{weight_B}{80.91g/mol}}=\dfrac{1/28.05}{(1/28.05)+(1/80.91)}=0.7426\\
x_B=\dfrac{n_B}{n_A+n_B}=\dfrac{\dfrac{weight_B}{80.91g/mol}}{\dfrac{weight_A}{28.05g/mol}+\dfrac{weight_B}{80.91g/mol}}=\dfrac{1/80.91}{(1/28.05)+(1/80.91)}=0.2574\]
(b)\(P_A=x_A*P_A^*=0.7426*0.2atm=0.1485atm\\
P_B=x_B*P_B^*=0.2574*0.62atm=0.1596atm\)
(c)\(x_A=\dfrac{P_A}{P_A+P_B}=\dfrac{0.1485atm}{0.1485atm+0.1596atm}=0.4820\\
x_B=\dfrac{P_B}{P_A+P_B}=\dfrac{0.1596atm}{0.1485atm+0.1596atm}=0.5180\\
P_A=x_A*P_A^*=(0.4820)(0.2atm)=0.0964atm\\
P_B=x_B*P_B^*=(0.5180)(0.62atm)=0.3212atm\)
5.3: The Thermodynamics of Mixing
Q5.35a
Give a brief explanation for the lower vapor pressure of a solvent in presence of a solute from the entropy point of view. (Hint: Look at colligative property of lower vapor pressure).
S5.35a
The action of mixing a solvent and a solute leads is associated with an increase in entropy. The final solution therefore has a greater entropy than that of solvent, giving it less driving force for evaporation. This leads to the solvent's decrease in evaporation which results in a lower vapor pressure.
Q5.35b
Describe the process of vapor-pressure lowering from the colligative properties of solutions.
S5.35b
Suppose you have an ideal solution to which you can apply Raoult's law:
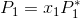
(Note: This solution has both a solvent and a solute which is nonvolatile).
Next, since we know that 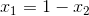 , we can ultimately rearrange the equation to be:
, we can ultimately rearrange the equation to be:
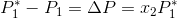
In the equation above, 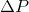 is directly proportional to the mole fraction of the solute.
is directly proportional to the mole fraction of the solute.
Q5.35c
Sugar is added to water. Would there be more water molecules in the vapor above the sugar solution or in the vapor above the pure water?
S5.35c
We would expect more water molecules in the vapor above the pure water.
Q5.36
4.0 moles of a compound was added to 500 g of HCl. What was the freezing point of the pure solvent if the freezing point of the solution is 188.6 K. (Kf=\(.55\dfrac{K\cdot kg}{mol})\)
S5.36
\(T_f= 188.6K\\ m= \dfrac{4mol}{.500kg}= 8\dfrac{mol}{kg}\)
\[\bigtriangleup T= -(K_f\cdot m) \rightarrow T_i=T_f+[(k_f)(m)]= 188.6K+(.55\dfrac{K\cdot kg}{mol})(8\dfrac{mol}{kg}= 193K\]
Q5.36a
After dissolving a substance weighing 0.246 grams in 100.0 g of water, the freezing point of the solution went down 1K below that of the pure solvent. What would be the molar mass of this substance?
S5.36a
The following information is needed.
\[ \triangle T=K_fm_2 \\ K_{fH_2O} = 1.86 \]
Now solve for the molar mass of the solute.
\[ 1 \ K = 1.86 m_2 \\ m_2 = 0.538 \\ m_2 = mol \div kg \ of \ solvent \\ mol_2 = 0.538 \ mol \ kg^{-1} \cdot 0.1 \ kg \ of \ water \\ mol_2 = 0.0538 \ moles \ of \ substance \\ Molar \ Mass = 0.246 \ grams \ of \ substance \ \div \ 0.0538 \ moles \ of \ substance \\ \underline{Molar \ Mass = 4.572 \ g/mol} \]
Click here for more information on freezing point depression.
Q5.36b
5.525 grams of toluene is mixed with 20.0 grams of acetone. Calculate the freezing point of acetone. The freezing point of the solution is found to be -102.6o C. The Kf of acetone is 2.40 oC kg/mol, and the molar mass of toluene is 92.14 g/mol
S5.36b
We can relate the molality of the solution to the freezing point depression:
\[m=\dfrac{\Delta T}{K_{f}}\]
Rearranged:
\[\Delta T=K_{f}m\]
\[T_{acetone}-T_{solution}=K_{f}m\]
\[T_{acetone}=T_{solution}+K_{f}\dfrac{mols \,of \,toluene}{kg\,of\, solvent}\]
\[=-102.6^{\circ}C+(2.40\dfrac{^{\circ}C}{kg\cdot mol})\dfrac{(5.252g\times \dfrac{1 mol}{92.14g})}{20.0\times 10^{-3}kg}\]
\[=-95.8^{\circ}C\]
Q5.37a
Two aqueous urea solutions have osmotic pressures of 1.4 atm and 3.0 atm, respectively, at a certain temperature. What is the osmotic pressure of a solution prepared by mixing equal volumes of these two solutions at the same temperature?
Q5.37b
A lab technician has 2 solutions of ammonia. Solution A exerts an osmotic pressure of 8 atm. When it is mixed with solution B in equal volume to produce solution C, it is determined that solution C exerts an osmotic pressure of 6.5 atm. What is the osmotic pressure of solution B?
Q5.38
A research scientist used 50 mL of sterilized water to conduct experiments and obtained odd results. She suspected that it had been contaminated with another compound and determined that the boiling point of the solution had increased to 105oC. How many moles of the compound (assume it dissolves as a molecule) had been added to the water?
Q5.39
Time-released pills are designed to have longer effect at a constant rate. The active ingredient is concealed by insoluble substances so that the active ingredient has to be dissolved by getting through the holes of insoluble layers covering outside. Explain how the insoluble layers regulate the absorption of the active ingredient.
Q5.41
Acetic Acid can make hydrogen bonds with water molecules and also with benzene. A solution of 4.0 g of acetic acid in 95g \(C_6H_6\) has a freezing point of \(3.5^oC\). What is the molar mass of the solute?
S5.41
\[\Delta T=K_fm\]
\(m=molality\)
\[3.5^oC=(5.12^oC\,kg\,mol^{-1})(m)\]
\[m=.68359mol\,kg^{-1}\]
\[m=\dfrac{moles\,solvent}{kg\,solvent}\]
\[moles\,solvent=.71757moles\]
\[mol\,acetic\,acid=\dfrac{g\,acetic\,acid}{molar\,mass,acetic\,acid}\]
\[7.1957\,moles=\dfrac{4.0g\,acetic\,acid}{.555887g\,mol^{-1}}\]
Q5.43
Determine on whether each of the following statements is true or false and briefly explain your answers. (a) Colligative properties depends on both the number of solute molecules and the size of the solute molecules. (b) The addition of a nonvolatile solute to a solvent only changes the chemical potential of liquid \((\mu _1(l))\). (c) The mole fraction of a component is never the same as the activity of the same component.
S5.43
- False; the definition of colligative properties are properties that ONLY depend on the number of solute molecules.
- True; \(\mu_1(s)\) and \(\mu_1(g)\) are not affected because solute is nonvolatile and insoluble to the solid solvent. (c) False; in the case of ideal solutions, the activity coefficient \((\gamma _i)\) is 1 and \(a_i =(1)*x_i\).
Q5.45
Provide an example of a nonideal solution explain why it is nonideal.(Hint: Look over the concept of nonideal solutions)
S5.45
An example of a non-ideal solution is a mixture of diethyl ether and water. Diethyl ether is a non-polar solvent used for dissolving organic molecules whereas water is polar. Intermolecular forces between these two components are weak; hence they will form two layers upon mixing; making the mixture a non-ideal solution.
Q5.46a
An unknown substance has a molal boiling-point elevation constant, Kb of 1.23 K/m. Find the molar mass of this substance. The enthalpy of vaporization for this substance is 38.56 kJ/mol at 78.37 oC.
S5.46a
For any substance:
\[K_{b}=\dfrac{RT_{0}^{2}\mathfrak{M}_{1}}{\Delta _{vap}\bar{H}}\]
Rearranging this equation, we get:
\[\mathfrak{M}_{1}=\dfrac{K_{b}\Delta _{vap}\bar{H}}{RT_{0}^{2}}\]
\[=\dfrac{(1.23\dfrac{K}{mol})(38.56\times 10^{3}\dfrac{J}{mol})}{(8.3145\dfrac{J}{K\cdot mol})(78.37+276.15)^{2}K}\]
\[=0.04616 \dfrac{kg}{mol}=46.16\dfrac{g}{mol}\]
Q5.46b
Find Kb (the molal boiling-point elevation constant) for acetone solution at 56ºC, given that:
\[ \triangle _{vap}\overline{H}^{\circ}_{Acetone} = 31.3 \ kJ \ mol^{-1}\]
S5.46b
You need to use the following equation:
\[ K_b = \dfrac{RT_{b}^{2}M_{molar}}{\triangle_{vap}\overline{H}}\]
Plug in values and solve for the Kb.
\[ \begin{align}
&K_b = \dfrac{(\dfrac{8.3145}{1000} \ kJ \ mol^{-1} \ K^{-1})(298K)^{2}(\dfrac{58.08}{1000}\ kg \ mol^{-1})}{31.3 \ kJ \ mol^{-1}} \\
& \underline{K_b = 1.37 K \ mol^{-1} \ kg}
\end{align} \]
Click here for more information on boiling point elevation.
Q5.47a
A home gardener and amateur scientist decides to prepare her olives by brining them. She begins the process by soaking the olives in fresh water. During this time she notices that the olives absorb moisture and swell. She then soaks the olives in a strong salt brine. During this time, she notices that the olives lose moisture and shrink. To what physical process can she attribute the shrinking and swelling? Why do the olives absorb the fresh water and lose moisture to the brine?
S5.47a
The movement of water in and out of the olives is due to diffusion. The high concentration of solutes in the brine relative to the concentration in the olives causes water to diffuse from olives into the brine, and the low concentration of solutes in the fresh water surrounding the olives causes the fresh water to diffuse into the olives, which have a comparatively high concentration of solutes.
Q5.47b
Describe the difference between a hypertonic, and hypotonic. Why does a cell shrink in a hypertonic solution, and expand in a hypotonic solution.
Q5.48
The following data give the pressures for water-methanol solution at 39.9oC. Find the activity coefficients of both components based on:
- Raoult's law
- Henry's law
|
xwater |
0 |
0.0490 |
0.3120 |
0.4750 |
0.6535 |
0.7904 |
|
Pwater/torr |
0 |
4.51 |
23.03 |
31.53 |
39.78 |
44.81 |
|
Pmethanol/torr |
255.6 |
253.39 |
188.27 |
152.87 |
116.22 |
80.89 |
Q5.49
A solution is made up of some amount of sucrose (C12H22O11) and 1.03 kg water. Calculate the amount of sucrose (in grams) in solution if the solution freezes at -2ºC and the activity coefficient of sucrose is 0.789.
S5.49
\[\Delta T = K_{b}m\]
\[m = \dfrac{\Delta T}{K_{b}} = \dfrac{2K}{1.86\ K\ mol^{-1}\ kg}\]
\[m = 1.075 mol kg^{-1}\]
a is effective molar concentration so a = m in:
\[a = \gamma x\]
x is the actual amount of sucrose in solution, so
\[x = \dfrac{a}{\gamma} = \dfrac{1.075}{0.789}\]
\[x = 1.36 mol \ kg^{-1}\]
\[mass\ sucrose = (\dfrac{1.36 mol}{kg\ H_{2}O})(1.03 kg\ H_{2}O)(\dfrac{342.3 g}{mol})\]
\[mass\ sucrose = 479 g\]
5.8: Ionic Activity
Q5.54
You know that the mean activity coefficient is 0.42. From this information find what the ionic strength of the compound LiNO2 is.
.gif?revision=1&size=bestfit&width=188&height=22)
.gif?revision=1&size=bestfit&width=229&height=22)
.gif?revision=1&size=bestfit&width=126&height=39)
I=0.548
Q5.56
A 0.15 m Ca(NO3)2 solution has a mean ionic activity coefficient of 0.17 at 25°C. Calculate the mean molality, the mean ionic activity, and the activity of the compound.
Q5.58
In 0.03m aqueous NaNO3 solution at temperature 300K., the size of the ionic atmosphere is 1/k, also known as Debye radius, is 27.8x10-10 m. Using the Debye radius formula to calculate the ionic strength I.
Q5.60
For a 0.0030m aqueous solution of \(CaCl_2\) at 298K, calculate the ionic strength. (a) Calculate the activity coefficients of \(Ca^{2+}\) and \(Cl^-\) ions in the solution and (b) calculate the mean ionic activity coefficients of these ions. (Hint: Use the Debye-Huckel limiting law)
S5.60
\[I=\dfrac{1}{2}\Sigma _im_iz^2_i\]
\[=\dfrac{1}{2}[(0.0030m)(2)^{2}+(0.0060m)(-1)^{2}]\]
\[=-.009m\]
(a)
\[log\gamma_i=-0.509z^2_i\sqrt{I}\]
For \(Ca^{2+}\),
\[log\gamma_+=-0.5092^2\sqrt{0.009}\]
\[log\gamma_+=-0.193\]
\[\gamma_+=.640985\]
For \(Cl^{-}\),
\[log\gamma_-=-0.509(-1)^2\sqrt{.009}\]
\[log\gamma_-=-0.048288\]
\[\gamma_-=.89477\]
(b)
\[\gamma _{\pm}=(\gamma _+^{v_{-}}\gamma _{-}^{v_{-}})^{\dfrac{1}{v}}=[(.640985)^{1}(.89477)^2]^{\dfrac{1}{3}}=.8006\]
Q5.65
For an ideal mixture, what mole fraction of each gas maximizes the entropy of mixing:
\[\Delta _{mix}S=-nR(x_{1}lnx_{1}+x_{2}lnx_{2})\]
Hint: Rewrite the above function in terms of only either x1 or x2, then derive.
S5.65
If we take the partial derivative of the entropy of mixing:
\[\Delta _{mix}S=-nR(x_{1}lnx_{1}+x_{2}lnx_{2})\]
\[\left [\dfrac{\delta \Delta _{mix}S}{\delta x_{1}} \right ]_{_{x_2}, n, R} =\left [-\dfrac{\delta }{\delta x_{1}}nR(x_{1}lnx_{1}+x_{2}lnx_{2}) \right ]_{x_{2}, n, R}\]
If we rewrite the function in terms of x1
\[=\left [-\dfrac{\delta }{\delta x_{1}}nR(x_{1}lnx_{1}+(1-x_{1})ln(1-x_{1}) \right ]_{x_{2}, n, R}\]
and derive using the chain rule:
\[=-\left (x_{1}\dfrac{1}{x_{1}}+lnx_{1}+(1-x_{1})\left (-\dfrac{1}{1-x_{1}} \right )+ln(1-x_{1})(-1) \right )\]
\[=1-lnx_{1}+1+ln(1-x_{1})\]
\[=-lnx_{1}+ln(1-x_{1})\]
\[=-ln\dfrac{x_{1}}{1-x_{1}}\]
To find the local maximum, we set this to 0 and solve for x1
\[0=-ln\dfrac{x_{1}}{1-x_{1}}\]
\[e^{0}=\dfrac{x_{1}}{1-x_{1}}\]
\[1=\dfrac{x_{1}}{1-x_{1}}\]
\[1-x_{1}=x_{1}\]
\[x_{1}=0.5\]
To check that this is a maximum and not a minimum, we plug in values to the left and right of the given x1 value (ex. 0.4 and 0.6). We then find that at x1<0.5 the derivative, or slope, is positive and at x1>0.5m the slope is negative. This is further confirmed by the following diagram, where .gif?revision=1&size=bestfit&height=10) is maximized at mole fraction 0.5.
is maximized at mole fraction 0.5.

Q5.64
The osmotic pressure arbitrary non-ideal diluted solution is measured at 2 different concentrations at 300K. At concentration of 5.20 g/L, osmotic pressure is 10.20 x 10-3 atm and at concentration of 8.90 g/L the osmotic pressure is 2.30 x 10-2 atm. Use this information to estimate the molar mass of the solute. (Hint: For dilute solutions, only the second virial coefficient is concerned. Look at equation for osmotic pressure and make a graph of π/c vs. c and look for the y-intercept of graph.)
S5.64
|
π (atm)
|
1.06 x 10-5 | 2.30 x 10-5 |
| c (g/L) | 5.20 | 8.90 |
|
π/c ( atm•L/g)
|
2.038 x 10-6 | 2.584 x 10-6 |
slope of the graph of π/c vs. c is generated as:
\[slope = \dfrac{(2.584 \times 10^{-6} - 2.038 \times 10^{-6}) \dfrac{atm \cdot L}{g}}{(8.90 - 5.20) \dfrac{g}{L}} = 1.476 \times 10^{-7} \dfrac{atm \cdot L^2}{g^2}\]
\[ \dfrac{\pi}{c} =\dfrac{RT}{M}(1+Bc) = \dfrac{RT}{M} + (\dfrac{RTB}{M})c \]
\[slope = \dfrac{RBT}{M} = 1.476 \times 10^{-7} \dfrac{atm \cdot L^{2}}{g^{2}}\]
Plug back into equation to solve for "y-intercept"
\[2.584 \times 10^{-6} = \dfrac{RT}{M} + ( 1.476 \times 10^{-7})(8.90) \]
\[ \Rightarrow \dfrac{RT}{M} = 1.271 \times 10^{-6} \dfrac{atm \cdot L}{g} \]
\[M = RT (1.271 \times 10^{-6} \dfrac{atm \cdot L}{g}) = (0.08206 \dfrac{L \cdot}{K \cdot mol})(300K)(1.271 \times 10^{-6} \dfrac{atm \cdot L}{g}) = {\color{red}3.13 \times 10^{-5} \dfrac{g}{mol}}\]
Q5.65
Assume that you have made an ideal solution of an unknown compound made of two components. Why does the mole fraction 0.5 achieve the maximum \(Δ_{mix}S\)?
S5.65
Use the equation.
\[ \Delta_{mix} S = -nR ( x_1 \ln x_1+x_2 \ln x_2 ) \]
Find the partial derivative since we want to find out the max value for this equation for x1 . We find x1 since it will show us x2.
\[\begin{align} [\dfrac{\partial }{\partial x_1} \Delta_{mix} S]_{x_2,n,R} &= [\dfrac{\partial }{\partial x_1}-nR \left( x_1 \ln x_1+x_2 \ln x_2 \right) ]_{x_2,n,R} \\ since & \ x_1+x_2 =1 \\ &= - [\dfrac{\partial }{\partial x_1}nR \left( x_1 \ln x_1+(1-x_1) \ln (1-x_1) \right) ]_{x_2,n,R} \\ derive & \\ &= -\left [(x_1 \cdot \dfrac{1}{x_1})+(\ln x_1)+ \left((1-x_1) \cdot \dfrac{-1}{1-x_1} \right ) + \left( (-1) \cdot \ln (1-x_1) \right ) \right] \\ &= -1- \ln x_1+1+ \ln (1-x_1) \\ &= \ln (1-x_1) - \ln x_1 \\ &= \ln \dfrac{1-x_1}{x_1} \end{align}\]
Now that we have the partial derivative, we set it to 0 and solve to attempt to find the maximum value.
\[\begin{align} & 0 = \ln \dfrac{1-x_1}{x_1} \\ &e^{0} = e^{\ln \dfrac{1-x_1}{x_1}} \\ &1 =\dfrac{1-x_1}{x_1} \\ &x_1 = 1-x_1 \\ &2x_1 = 1 \\ &\underline{x_1 = 0.5} \end{align}\]
Now we know that x1 = 0.5 is either a min or max. If we plug in a number smaller then 0.5 and bigger than 0.5 into the partial derivative we found earlier, we can conclude that the slope of the equation is positive to the left of 0.5 and negative to the right of the equation. This is characteristic of maximum values. Thus x1 = 0.5 and x2 = 0.5 attain the maximum values of ΔmixS since
x1 = 0.5 is a max.
See here for more details about ΔmixS. See figure (11) on that page for more details about the max.
Q5.66
Producing a certain gas mixture involves mixing high-pressure nitrogen and low-pressure hydrogen together. In one such production, 3.22 moles of N2 at 4.2 atm are mixed with 1.25 moles of H2 at 0.8 atm. Determine the change in Gibbs’ free energy.
5.9: Colligative Properties of Electrolyte Solutions
Q5.72
You are trying to produce a passive reverse osmosis system to obtain pure water from the ocean by using a semi-permeable membrane on one end of the intake pipe. At what depth would the bottom of the pipe need to be in order for pure water to begin to fill the pipe? Assume the ocean temperature is 17ºC, and the seawater is a 0.70 M NaCl solution. The density of seawater is 1.03 g/cm3.

