12: Molecules and Bonds (Exercises)

This is a set of problems that are organized to accompany the future "Physical Chemistry" textmap organized around Silbey et al. textbook.

Q12.2

The equilibrium distances in NaH, LiH, and KBr respectively, are 0.189 nm, 0.202 nm, and 0.282 nm. Find the effective fractional charges on the H and K ions.

Q12.6b

The overlap integral, \(S\) for the \(H_2^+\) molecule can be evaluated as

\[ S = \left(1+\dfrac{R}{a_0}+\dfrac{R^2}{3a_0^2}\right)e^{-R/a_0}\]

a function of \(R/a_0\). At what value of \(R\) is \(S\) minimized? What is the value of \(S\) at a separation of R=106 pm ?

Q12.6

The exchange integral for the \(H_2^+\) molecule can be evaluated as

\[ K = e^{\frac{-R}{a_o}} \left(\dfrac{a_o}{R} - \dfrac{2R}{3a_o} \right) \]

Plot this as a function of R/a_o. At what value of R is it at a minimum? What is the value of K at the equilibrium separation, R=106 pm?

S12.6b

The equation can be rewritten as

\[ k = e^{\frac{-R}{a_o}} \left(\frac{1}{R/a_o} - (2/3)(R/a_o) \right) \]

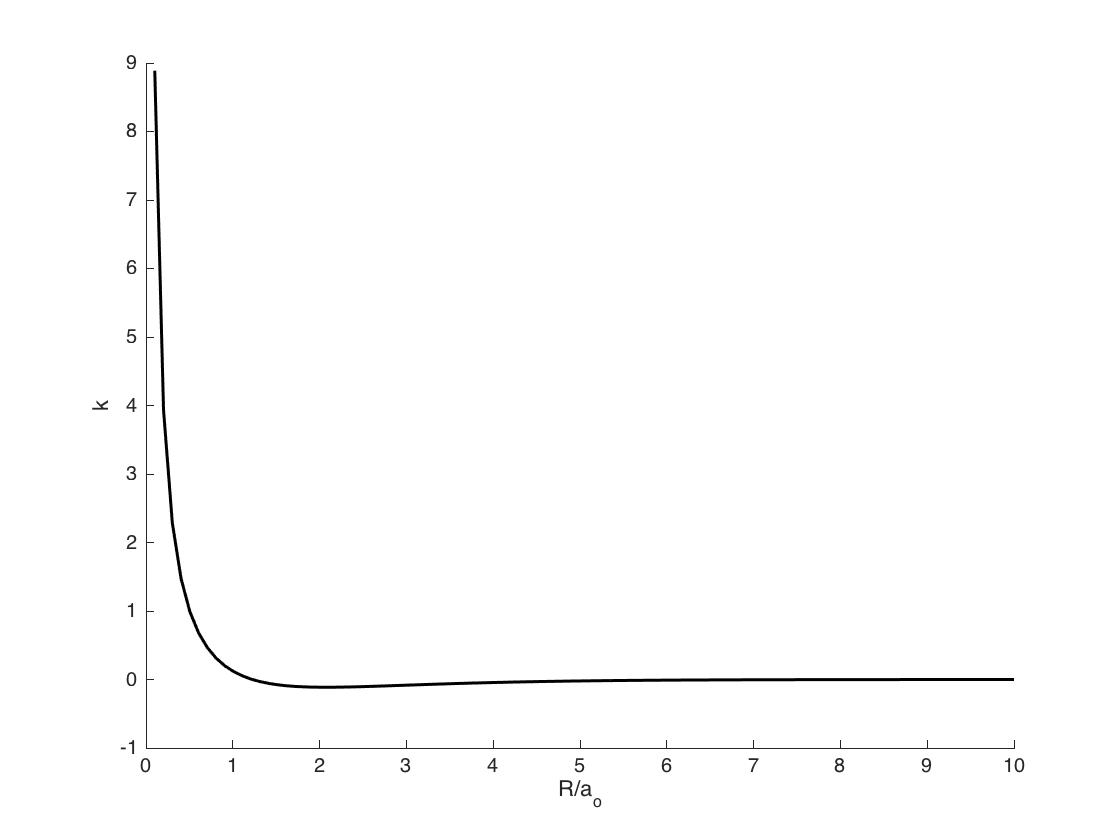
The minimum occurs at R/a_o=2.12, k=-.113.

a_o is the Bohr radius with value 52.9 pm.

Therefore, the minimum k occurs with R = 112.21 pm.

When R = 106 pm, R/a_o = 2.00 and k = -0.113.

Q12.22

A excited state of \(O_2^*\) is formed by exciting a single electron in \(O_2\) from the molecular orbital \(1\pi_g\) to the orbital \(3\sigma_u\). Note that \(^*\) is used to represent an excited state species, not an antibonding molecular orbital.

1. Write the electron configuration.
2. What are the possible spin states?
3. What is the bond order of \(O_2^*\)?
4. Is the electronic state of \(O_2^*\) gerade (\(g\)) or ungerade (\(u\))?

S12.22

(a)

Ground state electron configuration for \(O_2\): \((1\sigma_g)^2(1\sigma_u)^2(2\sigma_g)^2(2\sigma_u)^2(1\pi_u)^4(3\sigma_g)^2(1\pi_g)^2\)

The electron configuration for \(O_2^*\): \((1\sigma_g)^2(1\sigma_u)^2(2\sigma_g)^2(2\sigma_u)^2(1\pi_u)^4(3\sigma_g)^2(1\pi_g)^1(3\sigma_u)^1\)

(b)

Possible Spin States:

Using:

$$(1\pi_g)^1(3\sigma_u)^1\]

$$S=\mid\dfrac{1}{2}-\dfrac{1}{2}\mid\mbox{ ,..., }\dfrac{1}{2}+\dfrac{1}{2}\]

$$S=0,1\]

Therefore, the multiplicity

$$2S+1=1\mbox{ or }3\mbox{ (singlet or triplet) }\]

(c)

$$\mbox{Bond Order}=\dfrac{\mbox{# of electrons in bonding MO - # of electrons in antibonding MO}}{2}\]

Bonding MO: $$(2\sigma_g)^2(1\pi_u)^4(3\sigma_g)^2\]

Antibonding MO: $$(2\sigma_u)^2(1\pi_g)^1(3\sigma_u)^1\]

\[\mbox{Bond Order}=\dfrac{8-4}{2}=2\]

(d)

The electronic state is ungarade (\(u\)).

$$(1\pi_g)^1(3\sigma_u)^1\]

$$g\cdot u=u\]

Q12.22a

The first excited states of \(H_2^-\) are formed by exciting an electron from the antibonding \(1\sigma_u\) molecular orbital to the bonding \(2\sigma_g\) orbital. Write the electron configuration. What are the possible spin states? What is the bond order? Are the electronic states g or u?

S12.22a

\(H_2^-\) is a three electron system with the electron configuration for the first excited state is \( (1\sigma_g)^2 (2\sigma_g)^1 \). The spin states are S = \(+1/2 -1/2 \pm1/2\). The bond order is \(\dfrac{3}{2}\). The spin state is \( ^2\Sigma_g\), so the electronic state is g.

Q12.22b

What is the electron configuration for the ground state of He₂? What is the bond order? What about the bond order of He₂⁺?

S12.22b

This is the electron configuration for the ground state of \(He_2\). There are 2 electrons in the bonding orbital, and 2 electrons in the antibonding orbital. The bond order can be calculated as follows:

\[\mbox{Bond Order} = \dfrac{1}{2}[(\mbox{# of electrons in bonding orbitals})-(\mbox{# of electrons in antibonding orbitals})]\]

Thus the bond order of \(He_2\) is

\[\dfrac{1}{2}[2 - 2]=0\]

For \(He_2\) the electron configuration is

\[(1\sigma_g)^{2}(1\sigma_u)^{1}\]

So the bond order is

\[\dfrac{1}{2}(2-1) = \dfrac{1}{2}\]

Q12.26

What is the value of \(\psi^2_g\) (The probability density of finding the electron) at either nucleus in \(Li^+_2\) using the below equation for \(\psi_g\) ? What is the value of \(\psi^2_g\) at the midpoint of the bond? Use \(R_e =106\; pm \) and \(S = 0.86\)

\[\psi_g = \dfrac{1}{\sqrt{2(1+S)}}(1s_a + 1s_b) \]

S12.26

First we have to figure out what \(1s_a\) and \(1s_b\) are. These are the 1s orbitals of hydrogen, or the hydrogenic radial functions. The difference between a and b are the fact if the orbitals are bonding or antibonding, but it should not matter in this case. The hydrogenic radial function of a 1s orbital is

\[R_{1,0} (r) = 2 \left(\dfrac{Z}{a_o}\right)^{3/2} e^{-\frac{Zr}{a_o}} \]

That, multiplied with the angular wave function (in this case \(Y_{0,0}\)) gives us the equation of the 1s orbitals of hydrogen.

\[Y_{0,0} = \dfrac{1}{\sqrt{4\pi}} \]

Here we have \(R_e=106 \; pm\), convert to meters \(R_e=106 \times 10^{-12}\). Z is the atomic number of the element, in this case \(Z=3\) for Lithium. \(a_o\) is the Bohr radius and is a constant.

Solving for radial function:

\[R_{1,0} (r) = 2 \left(\dfrac{3}{a_o} \right)^{3/2} \times e^{-\dfrac{(3)(106 \times 10^{-12})}{a_o}} \]

Plug this back into eq 9.27

\[\psi_g = \dfrac{1}{\sqrt{2(1+S)}}(2( 2 \left(\dfrac{3}{a_o} \right)^{3/2} \times e^{-\dfrac{(318 \times 10^{-12})}{a_o}}\dfrac{1}{\sqrt{4\pi}})) \]

plug in \(S= 0.86\) into the equation

\[\psi_g = \dfrac{1}{\sqrt{2(1+.86)}}(2( 2 \left(\dfrac{3}{a_o}\right)^{3/2} \times e^{-\dfrac{(318 \times 10^{-12})}{a_o}})\dfrac{1}{\sqrt{4\pi}}) \]

Square \(\psi_g\) to get your final answer

\[\psi^2_g = (\dfrac{1}{\sqrt{3.72}}( 4 \left(\dfrac{3}{a_o}\right)^{3/2} \times e^{-\dfrac{(318 \times 10^{-12})}{a_o}})\dfrac{1}{\sqrt{4\pi}}))^2 \]

\[\psi^2_g = \dfrac{9.24}{a_o^2} \times e^{-\dfrac{636 \times 10^{-12}}{a_o}} \]

For the midpoint, use \(R_e=53\; pm \)

\[\psi^2_g = (\dfrac{1}{\sqrt{3.72}}(4(\dfrac{3}{a_o})^{3/2} \times e^{-\dfrac{(159 \times 10^{-12})}{a_o}})\dfrac{1}{\sqrt{4\pi}}))^2 \]

\[\psi^2_g = \dfrac{9.24}{a_o^2} \times e^{-\dfrac{318 \times 10^{-12}}{a_o}} \]

Q12.27a

Give the electronic configurations and bond orders for the ground states of N₂⁺ and O₂⁺ found by removing an electron from the highest filled molecular orbital. Explain any differences between the two ground states (besides the fact that N₂⁺ and O₂⁺ have a different number of electrons).

S12.27a

The ground state of \(N_2^+\) is simply the ground state of \(N_2\) with an electron removed from its highest filled molecular orbital:

\[(1s\sigma_{g}^2)(1s\sigma_{u}^{*2})(2s\sigma_{g}^{2})(2s\sigma_{u}^{*2})(2p_x\pi_{u}^{2})(2p_y\pi_{u}^{2})(2p_z\sigma_{g}^{1})\]

The bond order is determined by the following equation:

\[Bond\:order\: =\: \dfrac{Number\:of\:bonding\:electrons\: -\: Number\: of\: antibonding\: electrons}{2}\]

\[ Bond\: order\: of\: N_{2}^{+} = \dfrac{9-4}{2} = \dfrac{5}{2} \]

The ground state of \(O_2^+\) is simply the ground state of \(O_2\) with an electron removed from its highest filled molecular orbital:

\[(1s\sigma_{g}^2)(1s\sigma_{u}^{*2})(2s\sigma_{g}^{2})(2s\sigma_{u}^{*2})(2p_z\sigma_{g}^{2})(2p_x\pi_{u}^{2})(2p_y\pi_{u}^{2})(2p_x\pi_{g}^{*1})\]

\[Bond\: order\: of\: O_{2}^{+} = \dfrac{10-5}{2} = \dfrac{5}{2} \]

N₂⁺ has a smaller \(\Delta E\) between the \(2p_z\sigma_{g}\) orbital and the \(2s\sigma_{u}^{*}\) orbital which allows for enough orbital mixing to raise the energy of the \(2p_z\sigma_{g}\) orbital above that of the \(2p_x\pi_{u}\) and \(2p_y\pi_{u}\) orbitals. \(O_2^+\) has a larger \(\Delta E\) which prevents this from occurring. The larger \(\Delta E\) is due to the greater positive charge of the \(O_2^+\) nuclei which causes the energy of the s orbitals to be lowered more significantly than the p orbitals.

Q12.27b

What is the electron configuration for

1. \(Li^+_2\)
2. \(Be^+_2\)
3. \( B^+_2\)
4. \(N^+_2\)

Q12.27c

Find the electron configuration and bond order of the following

1. \(O_2^+\)
2. \(O_2\)
3. \(C_2\)
4. \(H_2^+\)