11: Quantum Atoms (Exercises)
- Page ID
- 41196
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This is a set of problems that are organized to accompany the future "Physical Chemistry" textmap organized around Silbey et al. textbook.
Q11.2
How much energy (in eV) is required to remove an electron from each of the following orbitals in a hydrogen atom:
- 2p
- 4d
- 5s
- 6p
S11.2
The removal of an electron from a Hydrogen atom is akin to moving an electron from energy state n to a distance infinity. The energy required for this is called the ionization energy which is equivalent (with the possible exception of a sign change depending on how ionization energy is defined) to the energy of a one-electron atom like the Hydrogen atom. Thus, solve for the desired energy using the following equation for the energy of a one-electron atom where Eh is the Hartree energy:
\[E_n = \dfrac{Z^2 E_h}{2 n^2}\]
- \(E_2 = \dfrac{(1)^2 (27.211\;eV)}{2 (2)^2} = 3.40\;eV\)
- \(E_4 = \dfrac{(1)^2 (27.211\;eV)}{2 (3)^2} = 0.850\;eV\)
- \(E_5 = \dfrac{(1)^2 (27.211\;eV)}{2 (4)^2} = 0.544\;eV\)
- \(E_6 = \dfrac{(1)^2 (27.211\;eV)}{2 (5)^2} = 0.378\;eV\)
Q11.3
Calculate the ground-state ionization potentials for He+, Li2+, Be3+, B4+ and C5+. Without any calculation, which would you expect to be highest and why?
S11.3
\[E_n= -(13.6eV) \dfrac{Z^2}{n^2}\]
(n=1 for all cases)
Ionization energy is approximately equal to the energy of the electron, se expect the ion with the highest Z value to have the highest ionization energy – more protons are acting on the electron thus holding it “tighter” to the nucleus, and with more force.
For He+
\[E_{He^+} = -(13.6eV) \dfrac{2^2}{1^2} =-54.4eV\]
For Li2+
\[E_{Li^{2+}} = -(13.6eV) \dfrac{3^2}{1^2} =-122.4eV\]
For Be3+
\[E_{Be^{3+}} = -(13.6eV) \dfrac{4^2}{1^2} =-217.6eV\]
For B4+
\[E_{B^{4+}} = -(13.6eV) \dfrac{5^2}{1^2} =-340eV\]
For C5+
\[E_{C^{5+}} = -(13.6eV) \dfrac{6^2}{1^2} =-489.6eV\]
Q11.06
Show that the product of a (non-normalized) Gaussian function centered at \(R_A\) and one centered at \(R_B\).
For example:
\[\phi_1=\exp{-\alpha \left | r-R_A \right |^2}\\\\
\phi_2=\exp{-beta\left | r-R_B \right |^2}\\\
\\R_P=\dfrac{\alpha*R_A + \beta*R_B}{\alpha +\beta}\\\]
\[\phi_1=\exp{-\alpha \left | r-R_A \right |^2}\\\\ \phi_2=\exp{-beta\left | r-R_B \right |^2}\\\ \\R_P=\dfrac{\alpha*R_A + \beta*R_B}{\alpha +\beta}\\\]
Note that this is a Guassian function Centered at the RpS11.06
1st, the given equations turn into these below in one dimemsion
\[\phi_1=\exp{-\alpha \left | x-x_A \right |^2}\\\\ \phi_2=\exp{-beta\left | x-x_B \right |^2}\\\ \\x_p=\dfrac{\alpha*x_A + \beta*x_B}{\alpha +\beta}\\\]
2nd, showing φ1 times φ2 is the easiest way to show that they can be written as the Gaussian function centered at x_p.
therefore:
\[\phi_1*\phi_2=\exp({-\alpha(x-x_A)^2-\beta(x-x_B)^2})\\ \phi_1*\phi_2=\exp(-\alpha*x^2+\alpha*x*2x_A-\alpha*x_A^2-\beta*x^2+\beta*x*2x_A-\beta*x_A^2)\\\ \phi_1*\phi_2=\exp[(-(\alpha*x^2+beta*x_A^2)]*\exp[-(\alpha +\beta)*x^2+2x(x_A*\alpha +x_B*\beta )]\\\]
\[\phi_1*\phi_2=\exp[(-(\alpha*x^2+beta*x_A^2)]*\exp[-(\alpha +\beta )[x^2-2x\dfrac{\alpha *x_A+\beta *x_B}{\alpha +\beta }+\dfrac{\alpha x_A+\beta x_B}{\alpha +\beta }]*exp[(\alpha +\beta )\dfrac{\alpha *x_A+\beta *x_B}{\alpha +\beta }))]\\\ \phi_1*\phi_2=\exp[(-\dfrac{\alpha*\beta (x_A-x_B)^2}{\alpha +\beta }]*exp[-(\alpha +\beta )(x-x_p)^2]\]
Therefore, this above is a Guassian function centered at xp.Q11.6a
A hydrogenlike atom has a series of spectral lines at λ = 26.2445 nm, λ = 19.4404 nm, λ = 17.3578 nm, and λ = 16.4028nm. What is the nuclear charge on the atom? What is the formula for this spectral series (i.e. in term of \(n_1\) and \(n_2\))?
S11.6a
We know that: $$E=\dfrac{-e^2}{8\pi*e_0*a_0*n^2}=\dfrac{h*c}{λ}\]
Q11.6 b
A hydrogenlike atom has a series of spectral lines at λ= 26.2445 nm, λ= 19.4404 nm, λ= 17.3578 nm, and λ= 16.4028nm. What is the formula for this spectral series?
S11.6b
Rydberg Formula for any hydrogen-like element
\[\dfrac{1}{λ} = R_h·Z^2 \left(\dfrac{1}{n1^2}-\dfrac{1}{n2^2}\right)\]
Q11.6c
A hydrogen atom has a series of spectral lines at \(\lambda_1 = 95.0nm\), \(\lambda_2 = 97.3nm\), \(\lambda_3 = 102.6nm\), and \(\lambda_4 = 121.6nm\). What type of Rydberg series do these values correspond to? What n values does each wavelength represent (i.e., \(n_1\) and \(n_2\) in the Rydberg formula)?
S11.6c
In order to answer the first part of this problem, we need to answer the second question.
The Rydberg formula for hydrogen:
\[\dfrac{1}{\lambda}=R\left(\dfrac{1}{n^2_1}-\dfrac{1}{n^2_2}\right)\]
where R is the Rydberg constant, approximately \(1.097\times10^{7}m^{-1}\)
We know that \(n_1=1\). We can start by plugging in \(\lambda_1\) and solve for its corresponding \(n_2\) value:
\[\dfrac{1}{95.0\times10^{-9}m}=(1.097\times10^7m^{-1})\left(1-\dfrac{1}{n^2_2}\right) \Longrightarrow n_2=4.97=5\]
Plug in remaining \(\lambda\) values and we get the following corresponding \(n_2\) values:
\[\lambda_1 = 95.0nm \Longrightarrow n_2=5\]
\[\lambda_2 = 97.3nm \Longrightarrow n_2=4\]
\[\lambda_1 = 102.6nm \Longrightarrow n_2=3\]
\[\lambda_1 = 121.6nm \Longrightarrow n_2=2\]
Since the lowest \(n_2\) value is 2, we know that this series corresponds to a Lyman series.
Q11.6d
The perturbation to the H atom's Hamiltonian is
\[\hat{H}^{(1)}=\dfrac{e}{2m_e}*B_{Z}(\hat{L}_{Z}+2\hat{S}_{Z})\]
Using the spin states of the atom below, which are eigenfunctions of the Hamiltonian.
\[\Psi_{2,0,0 \dfrac{1}{2}}=\Psi_{2,0,0}(r) \alpha\]
\[\Psi_{2,0,0-\dfrac{1}{2}}=\Psi_{2,0,0}(r) \beta\]
Calculate the Energies of both states of the Hydrogen-like atom in the field.
S11.6d
\[E=E^{(0)}+E^{(1)}\]
First, Use the Energy Equation to find the Energy 0:
\[E^{(0)}=(n+1/2)\hbar* \omega\]
\[(atomic-units ) \hbar = 1\]
\[E^{(0)}=-1/2\]
Now find the Energy for E1 for alpha
\[E^{(1)}=\dfrac{eB_Z}{2m_e}\langle \Psi_{2,0,0} \alpha \mid \hat{L}_Z+2*\hat{S}_Z\mid \Psi_{2,0,0} \alpha \rangle\]
Separate the Psi into Spherical Harmonics and Hydrogenic Radial Functions and the Angular Momentum Operators and Spin Angular Momentum:
\[E^{(1)}=\dfrac{B_Z}{2}\langle R_{2,0}Y_{0,0} \mid \hat{L}_Z\mid R_{2,0}Y_{0,0} \rangle+2 \langle \alpha \mid \hat{S}_z \mid \alpha \rangle\]
Angular Momentum Operators Eigenvalue is
\[\hat{L}_Z= m\hbar\]
Spin Angular Momentum Operators Eigenvalue is
\[\hat{S}_Z=\dfrac{1}{2}\]
when dealing with alpha
\[E^{(1)}=\dfrac{B_Z}{2}\langle R_{2,0}Y_{0,0} \mid m \hbar \mid R_{2,0}Y_{0,0} \rangle+2 \langle \alpha \mid \dfrac{\hbar}{2}\mid \alpha \rangle\]
\[(atomic-units ) \hbar = 1; m=0\]
\[E^{(1)}=\dfrac{B_Z}{2}\]
\[E_{total}=\dfrac{-1}{2}+\dfrac{B_Z}{2}\]
Now find the Energy for E1 for beta:
\[E^{(1)}=\dfrac{eB_Z}{2m_e}\langle \Psi_{2,0,0} \beta \mid \hat{L}_Z+2*\hat{S}_Z\mid \Psi_{2,0,0} \beta \rangle\]
Separate the Psi into Spherical Harmonics and Hydrogenic Radial Functions and the Angular Momentum Operators and Spin Angular Momentum:
\[E^{(1)}=\dfrac{B_Z}{2}\langle R_{2,0}Y_{0,0} \mid \hat{L}_Z\mid R_{2,0}Y_{0,0} \rangle+2 \langle \beta \mid \hat{S}_z \mid \beta \rangle\]
Angular Momentum Operators Eigenvalue is
\[\hat{L}_Z= m\hbar\]
Spin Angular Momentum Operators Eigenvalue is
\[\hat{S}_Z=\dfrac{-1}{2}\]
when dealing with beta
\[E^{(1)}=\dfrac{B_Z}{2}\langle R_{2,0}Y_{0,0} \mid m \hbar \mid R_{2,0}Y_{0,0} \rangle+2 \langle \beta \mid \dfrac{- \hbar}{2} \mid \beta \rangle\]
\[(atomic-units ) \hbar = 1; m=0\]
\[E^{(1)}=\dfrac{B_Z}{2}\]
\[E_{total}=\dfrac{-1}{2}-\dfrac{B_Z}{2}\]
Q11.8
Calculate the wavelength of the emitted light in result of the electron's transition from 3s to 2p for \(C^{+5}\).
S11.8
Since it's a hydrogen-like atom, use Bohr's Theory:
\[∆E = R_h\left(\dfrac{1}{n^2_i} - \dfrac{1}{n^2_f}\right)\]
\[R_h=2.08x10^{-18} J\]
\[∆E = 2.08x10^{-18}J \left(\dfrac{1}{3^2} - \dfrac{1}{2^2}\right)\]
\[∆E = -2.889x10^{-19} Joules\]
\[λ = \dfrac{ch}{-2.889x10^{-19}}\]
\[\dfrac{3.0x10^8 m*s^{-1} x 6.625x10^{-34}J*s}{2.89x10^{-19}J}\]
\[λ= 687nm\]
Q11.8
- Calculate the analytical solution for the distance from proton to electron in the 1s orbital of a Hydrogen-like atom.
- Compute numerical values of the same distance for Be2+ and C4+.
S11.8a
Solving for the expectation value of r, we start with the integral
\[\langle r \rangle = \int_{0}^\infty \psi_{100} r \psi_{100} dx dy dz\]
In terms of the \(Y\) and \(R\) components of \(\psi\), this is
\[ = \int_{0}^{2\pi} \int_{0}^\pi \int_{0}^\infty R_{1,0} r R_{1,0} Y_{0,0} Y_{0,0} r^2 sin(\theta) dr d\theta d\phi\]
Because \(Y\) does not depend on \(R\), it can be separated from the \(R(r)\) terms. These \(Y\) terms are normalized, so they become 1 and the integral equals
\[ = 1*\int_{0}^\infty 2(\dfrac{Z}{a_0})^{3/2} e^{-Zr/a_0} r^3 2(\dfrac{Z}{a_0})^{3/2} e^{-Zr/a_0} dr \]
Next, we combine terms to achieve
\[ = \int_{0}^\infty 4(\dfrac{Z}{a_0})^{3} e^{\dfrac{-2Zr}{a_0}} r^3 dr\]
\[ = 4(\dfrac{Z}{a_0})^3 \int_{0}^\infty e^\dfrac{-2Zr}{a_0} r^3 dr\]
Now we use the mathematical identity \[\int_{0}^\infty x^n e^{-ax} dx = \dfrac{n!}{a^{n+1}}\]
with \[n=3\] and \[a=\dfrac{2Z}{a_0}\]
Thus,
\[ = 4(\dfrac{Z}{a_0})^3 \dfrac{3!}{(\dfrac{2Z}{a_0})^4}\]
\[ = \dfrac{4*6}{16} (\dfrac{Z}{a_0})^3 (\dfrac{a_0}{Z})^4\]
And the analytical solution is
\[ = \dfrac{3a_0}{2Z}\]
S11.8b
For C4+, \(Z = 6\) and \(a_0 = 70*10^{-9}m\)
so \(\langle r \rangle_{C^{4+}} = 1.75*10^{-8}m\)
For Be2+, \(Z = 4\) and \(a_0 = 105*10^{-9}m\)
so \(\langle r \rangle_{Be^{2+}} = 3.94*10^{-8}m\)
Q11.8
Show that for a 1s orbital of a hydrogen-like atom the most probable distance from proton to electron is ao/Z. Find the numerical values for Li+ and Be2+.
S11.8
The wavefunction of a 1s orbital for a hydrogen-like ion is given by:
\[\psi_{1s} = \psi_{1,0,0} = R_{1,0}(r)Y_{0,0}(\theta,\phi) = \dfrac{1}{\sqrt{π}}(\dfrac{Z}{a_0})^{\dfrac{3}{2}}e^{\dfrac{-Zr}{a_0}}\tag{1}\]
\[a_0 = 5.29\times10^{-11}m\]
The radial probability density equation with this wavefunction is the following:
\[\langle \psi_{1,0,0}|r^2|\psi_{1,0,0} \rangle = \dfrac{1}{π}(\dfrac{Z}{a_0})^3r^2e^{\dfrac{-2Zr}{a_0}}\tag{2}\]
To find the most probable distance from proton to electron, take the derivative with respect to r of equation (2), set it equal to 0, and solve for r.
\[\dfrac{d}{dr}\langle \psi_{1,0,0}|r^2|\psi_{1,0,0} \rangle = \dfrac{d}{dr}(\dfrac{1}{π}(\dfrac{Z}{a_0})^3r^2e^{\dfrac{-2Zr}{a_0}})\]
\[\dfrac{d}{dr}\langle \psi_{1,0,0}|r^2|\psi_{1,0,0} \rangle = \dfrac{1}{\pi}(\dfrac{Z}{a_0})^3(2r-\dfrac{2Z}{a_0})e^{\dfrac{-2Zr}{a_0}}\]
\[\dfrac{1}{\pi}(\dfrac{Z}{a_0})^3(2r-\dfrac{2Z}{a_0})e^{\dfrac{-2Zr}{a_0}} = 0\]
\[2r-\dfrac{2Z}{a_0} = 0\]
\[r = \dfrac{a_0}{Z}\]
For Be2+, Z = 4. The most probable distance for Be2+ is
\[r = \dfrac{5.29\times10^{-11}m}{4} = 1.323m\]
For Li+, Z = 3. The most probable distance for Li+ is
\[r = \dfrac{5.29\times10^{-11}m}{3} = 1.763m\]
Q11.8
Show that for a 1s orbital of a hydrogenlike atom the most probable distance from proton to electron is \(a_0/Z\). Find the numberical values for \(N^{6+}\) and \(C^{3+}\).
S11.8
\[\dfrac{d}{dr} \Psi^*_{1s} \Psi_{1s} r^2_{mp} = 0\]
\[\dfrac{d}{dr} r^2_{mp} \dfrac{Z^3}{\pi a^3_0} e^{\dfrac{-2Zr_{mp}}{a_0}} = 0\]
\[2 r_{mp} e^{\dfrac{-2Zr_{mp}}{a_0}} + \dfrac{-2Zr^2_{mp}}{a_0} e^{\dfrac{-2Zr_{mp}}{a_0}} = 0\]
\[a_0 - Zr_{mp} = 0\]
\[r_{mp} = \dfrac{a_0}{Z}\]
\[a_0 = 5.29\times\ 10^{-11} m\]
\[r_{mp N^{6+}} = 5.29\times\ 10^{-11} m\]
\[r_{mp C^{3+}} = 1.76\times\ 10^{-11} m\]
Q11.8
Show that the expectation value for a 2P atom in a hydrogen-like species is: 5a0/Z. Then, find the numerical values for He+ and N6+
S11.8
first, find n,l, and m
for the 2nd orbital, n=2. For p, l=1. For simplicity, we can choose m=0
\[ \langle r \rangle= \langle\Psi_{210}|r|\Psi_{210} \rangle\]
\[ \langle r \rangle= \langle R_{21}|r|R_{21}><Y_{10}|Y_{10} \rangle\]
\(\langle Y_{10}|Y_{10} \rangle\) is equal to 1 by definition and can be ignored
\[R_{21}= \dfrac{1}{\sqrt{3}}(\dfrac{Z}{2a_0})^{3/2}\dfrac{Zr}{a_0}e^{(\dfrac{-Zr}{2a_0})}\]
Plugging in...
\[\langle R_{21}|r|R_{21} \rangle=\dfrac{1}{3}(\dfrac{Z}{2a_0})^{3}(\dfrac{Z^2}{a_0^2})\int^\infty_0r^5e^{\dfrac{-Zr}{a_0}}dr\]
from an integral equation sheet, the integral can be found as:\(\dfrac{120a_0^6}{Z^6}\)
\[\langle r \rangle=( \dfrac{1}{3})( \dfrac{1}{8})( \dfrac{Z^5}{a_0^5})( \dfrac{a_0^6}{Z^6})(120)\]
simplifying, we get that the expectation value of r = \( \langle r \rangle= \dfrac{5a_0}{Z}\)
- for He+ \(\langle r \rangle= \dfrac{5}{2}(5.29177*10^{-11}m)=132pm\)
- for N6+ \(\langle r \rangle= \dfrac{5}{7}(5.29177*10^{-11}m)=38pm\)
Q11.08
Show that for a 1s orbital of a hydrogen-like atom the most probable distance from proton to electron is a0/Z. Fine the numerical values for C5+ and B3+.
S11.08
\[\psi_{1s} = \psi_{1,0,0}(r,\theta,\phi) = R_{1,0}(r)Y_{0,0}(\theta,\phi) = \dfrac{1}{\sqrt{\pi}}(\dfrac{Z}{a_0})^{\dfrac{3}{2}}exp(-Zr/a_0)\]
Where Z is the atomic number and a0 is the Bohr radius(5.29x10-11m).
The radial probability density for this state is:
\[\langle \psi_{1,0,0}|r^2|\psi_{1,0,0} \rangle= \dfrac{1}{\pi}(\dfrac{Z}{a_0})^3r^2exp(-Zr/a_0)\]
To find the most probable distance from proton to electron,
\[\dfrac{d}{dr}\langle \psi_{1,0,0}|r^2|\psi_{1,0,0} \rangle = \dfrac{d}{dr}(\dfrac{1}{\pi}(\dfrac{Z}{a_0})^3r^2exp(-Zr/a_0)\]
\[\dfrac{d}{dr}\langle \psi_{1,0,0}|r^2|\psi_{1,0,0} \rangle = \dfrac{1}{\pi}(\dfrac{Z}{a_0})^3(2r-\dfrac{2Z}{a_0}exp(-Zr/a_0)\]
\[\dfrac{1}{\pi}(\dfrac{Z}{a_0})^3(2r-\dfrac{2Z}{a_0})exp(-Zr/a_0) = 0\]
\[2r-\dfrac{2Z}{a_0} = 0\]
\[r = \dfrac{a_0}{Z}\]
For C5+ (Z = 7),
\[r = \dfrac{5.29\times10^(-11) m}{7} = 1.058\times10^{-11} m\]
For B3+ (Z = 5),
\[r = \dfrac{5.29\times10^(-11) m}{5} = 7.557\times10^{-12} m\]
Q11.9a
Find the value of r for which the hydrogenlike atom 3p wavefunction is zero. Also find \(\theta\) for which the 3p wavefunction is zero. (There are the radial and angular nodes)
S11.9a
The wavefunction for both case would be:
\[\psi_{310}= \dfrac{1}{81} (\dfrac{2}{\pi})^{1/2} (\dfrac{Z}{a_0})^{3/2} (6\sigma-\sigma^2)e^{-\sigma/3}cos \theta \]
where:
\[\psi_{310}= \dfrac{Zr}{a_0} \]
Making :
\[ \psi_{310}=0 \]
\[\dfrac{1}{81} (\dfrac{2}{\pi})^{1/2} (\dfrac{Z}{a_0})^{3/2} (6\sigma-\sigma^2)e^{-\sigma/3} cos \theta = 0 \]
For "r" :
\[6\sigma-\sigma^2=6\dfrac{Zr}{a_0}-(\dfrac{Zr}{a_0})^{1/2}=0\]
\[6=\dfrac{Zr}{a_0}\]
\[r=\dfrac{a_0}{Z} \]
For "\(\theta\)":
\[cos\theta=0\]
\[\theta=90^{\circ}\]
Q11.9b
Find the values where hydrogen like atoms 1S and 2PX wave functions are equal to zero.
S11.9b
\[1S: \psi_{100}= \dfrac{1}{\sqrt{4\pi}}2\left(\dfrac{Z}{a_0}\right)^{\dfrac{3}{2}}e^{-\dfrac{Zr}{a_0}}\]
\[e^{-\dfrac{Zr}{a_0}}=0\]
\[r=\infty\]
there is no node on the 1S orbital
\[2P_X: \psi_{211} = -\left(\dfrac{1}{8\pi}\right)^{\dfrac{1}{2}} \sin \theta e^{i \phi} \left(\dfrac{Z}{2a_0}\right)^{\dfrac{3}{2}} \dfrac{Zr}{a_0} e^{-\dfrac{Zr}{2a_0}}\]
\[\dfrac{Zr}{a_0} e^{-\dfrac{Zr}{2a_0}}=0\]
\[\dfrac{Zr}{a_0} =0\]
\[r=0\]
\[\sin \theta = 0\]
\[\theta=0\]
\[e^{i \phi} = 0\]
\[\phi=\infty\]
Q11.9c
Calculate the radial nodes r for the electron of a hydrogen like atom in the 2p and 3d orbitals
S11.9c
\[\psi_{210}=\dfrac{1}{\sqrt{3}}(\dfrac{z}{2a_0})^{3/2}\dfrac{zr}{a_0}e^{(-zr)/(2a_0)}\sqrt{\dfrac{3}{4\pi}}cos\theta\]
\[0=\dfrac{1}{\sqrt{3}}(\dfrac{z}{2a_0})^{3/2}\dfrac{zr}{a_0}e^{(-zr)/(2a_0)}\sqrt{\dfrac{3}{4\pi}}cos\theta\]
\[r=0\]
\[\psi_{310}=\dfrac{4\sqrt{2}}{9}(\dfrac{z}{3a_0})^{3/2}\dfrac{zr}{a_0}(1-\dfrac{zr}{6a_0})e^{(-zr)/(3a_0)}\sqrt{\dfrac{3}{4\pi}}cos\theta\]
\[0=\dfrac{4\sqrt{2}}{9}(\dfrac{z}{3a_0})^{3/2}\dfrac{zr}{a_0}(1-\dfrac{zr}{6a_0})e^{(-zr)/(3a_0)}\sqrt{\dfrac{3}{4\pi}}cos\theta\]
\[r=0, r=\dfrac{6a_0}{z}\]
Q11.9d
Solve for the radial nodes of the hydrogenlike atom 3p wave function, where the equation equals 0.
S11.9d
The radial probability function must equal zero. The 30 radial wave function is:
(√2/81ao3/2√π)[6-ρ]r/aoe-r/ 3aocosθ
ρ=2Zr/ (nao)=6
= 2(1)r/ 3ao=6
=2r/ao=18
=r/ao=9
=r=9ao
Q11.09
Find the values of r for which the hydrogenlike atom 2s and 3s wavefunctions are equal to zero (these are the radial nodes). Compare to Fig. 11.1.
S11.09e
For the 2s atom:
\[ \psi_{2,0,0} = R_{2,0}Y_{0,0} = (2 \left( \dfrac{Z}{2ao} \right)^{3/2} \left(1 - \dfrac{Zr}{2ao} \right)e^{- \dfrac{Zr}{ao}} )( \dfrac{1}{ \sqrt{4 \pi})} \]
\[ 0 = \left(2 \left( \dfrac{Z}{2ao} \right)^{3/2} \left(1 - \dfrac{Zr}{2ao} \right)e^{ \dfrac{-Zr}{ao}} \right)*( \dfrac{1}{ \sqrt{4 \pi})} \]
\[ ( 1 - \dfrac{Zr}{2ao} )e^{ \dfrac{-Zr}{ao}} \]
\[e^{ \dfrac{-Zr}{ao}} = \dfrac{Zr}{2ao} e^{ \dfrac{-Zr}{ao}} \]
\[ 1 = \dfrac{Zr}{2ao} \]
\[ r = \dfrac{2ao}{Z} \]
For the 3s atom: \[ \psi_{3,0,0} = R_{3,0}Y_{0,0} = \dfrac{1}{sqrt{4 \pi}}(2 \dfrac{Z}{3ao})^{3/2}*(1- \dfrac{2Zr}{3ao} + \dfrac{2Z^2r^2}{27ao^2})e^{ \dfrac{-Zr}{3zo}} \]
\[ 0 = 1 - \dfrac{2Zr}{3ao} + \dfrac{2Z^2r^2}{27ao^2} \]
We have to use the quadratic formula to find r: \[ r = - b \pm \sqrt{ \dfrac{b^2 - 4ac}}{2a}\]
\[ r = - \dfrac{18ao}{Z} \pm \dfrac{27ao}{2Z \sqrt{27}} \]
Q11.10
Find the expectation value for the radius of a 1s electron for (a) Li and (b) Be2+.
S11.10
Let's find the general equation for \(\langle r \rangle\) for a 1s electron.
A 1s electron has wave function,
\[\psi_{1,0,0}=R_{1,0}Y_{0,0}\]
Where
\[R_{1,0}=2(\dfrac{Z}{a_0})^{(3/2)}e^{(-Zr/a_0)}\]
and
\[Y_{0,0}=\dfrac{1}{\sqrt{4\pi}}\]
The expectation value \(\langle r \rangle\) is defined as
\[\langle r \rangle = \int_{0}^\infty \psi_{100} r \psi_{100} r^2 sin(\theta) dr d\theta d\phi\]
Substituting in \(R_{1,0}\) and \(Y_{0,0}\),
\[\langle r \rangle = \int_{0}^{2\pi} \int_{0}^\pi \int_{0}^\infty R_{1,0} r R_{1,0} Y_{0,0} Y_{0,0} r^2 sin(\theta) dr d\theta d\phi\]
Since \(Y_{0,0}\) does not depend on r, it can be separated from the \(R_{1,0}\) terms. Also, \(Y_{0,0}\) is normalized, so once integrated, you are left with
\[\langle r \rangle = 1\times \int_{0}^\infty 2(\dfrac{Z}{a_0})^{3/2} e^{-Zr/a_0} r 2(\dfrac{Z}{a_0})^{3/2} e^{-Zr/a_0} r^2 dr \]
Now, by combining like terms and pulling the constants out front, the integral becomes
\[\langle r \rangle = 4(\dfrac{Z}{a_0})^3 \int_{0}^\infty e^{-2Zr/a_0} r^3 dr\]
Now we can use the simple exponential integral identity,
\[\int_{0}^\infty x^n e^{-ax} dx = \dfrac{n!}{a^{n+1}}\]
with \(n=3\) and \(a=dfrac{2Z}{a_0}\).
This yields,
\[\langle r \rangle = 4(\dfrac{Z}{a_0})^3 \dfrac{3!}{(\dfrac{2Z}{a_0})^4} = \dfrac{4\times 6}{16} (\dfrac{Z}{a_0})^3 (\dfrac{a_0}{Z})^4\]
Simplifying,
\[\langle r \rangle = \dfrac{3a_0}{2Z}\]
Now that we have a general solution for \(\langle r \rangle_{1s}\), we can solve specifically for (a) and (b)
(a) For Lithium, \(Z=3\), thus
\[\langle r \rangle_{1s}=\dfrac{3a_0}{2\times 3}\]
Calculating,
\[\langle r \rangle_{1s} = \dfrac{a_0}{2}\]
(b) For Be2+, \(Z=4\), thus
\[\langle r \rangle_{1s}=\dfrac{3a_0}{2\times 4}\]
Calculating,
\[\langle r \rangle_{1s} = \dfrac{3a_0}{8}\]
Q11.10
What is the average distance an orbital electron to the nucleus for a 2s and 2p electron in
- \(He^+\)
- \(Li^{2+}\)
S11.10
Normalized wave function for electron in 2s orbital for H-like species is:
\[Ψ(2,0,0) = sqrt( 1/8 ) * ( Z/a_0 )^(3/2) (2-ρ) * e^(-ρ/2) * Y(0,0)\]
\[\rho=\dfrac{Zr}{a_{0}}\]
\[\langle r\rangle _{2s} = \]
\[\int_{0}^{+inf} r^{2} dr \int_{0}^{pi} sin\theta d\theta \int_{0}^{2*pi} d\varphi \varPsi^{*}_{2,0,0} r \varPsi^{*}_{2,0,0}\]
\[\dfrac{1}{8} ( \dfrac{Z}{a_{0}})^{3} \int_{0}^{+inf} r^{3} dr (2-\rho)^{2} e^{- \rho} \int_{0}^{pi}sin\theta d\theta \int_{0}^{2pi} d\varphi Y_{0,0}(\theta,\varphi)^{*}Y_{0,0}(\theta,\varphi)\]
\[\dfrac{1}{8} ( \dfrac{Z}{a_{0}})^{3} ( \dfrac{a_{0}}{Z})^{4} \int_{0}^{+inf} d\rho \rho^{3} (2-\rho)^{2} e^{-\rho}\]
\[\dfrac{1}{8} ( \dfrac{Z}{a_{0}}) \int_{0}^{+inf} d\rho(\rho^{5} -4\rho^{4} + 4\rho^{3})e^{-\rho}\]
\[\dfrac{1}{8} ( \dfrac{Z}{a_{0}}) (5! - 4\times4! + 4\times3!)\]
\[6 \dfrac{a_{0}}{Z}\]
\[\langle r\rangle _{2p} = \]
\[\varPsi_{2,1,0} = \dfrac{1}{2\sqrt{6}}(\dfrac{Z}{a_{0}})^{\dfrac{3}{2}}\rho e^{-\rho / 2}Y_{1,0}(\theta,\varphi)\]
\[\int_{0}^{inf} r^{2}dr \int_{0}^{pi} sin\theta d\theta \int_{0}^{2*pi} d\varphi \varPsi^{*}_{2,1,0}\varPsi_{2,1,0}\]
\[\dfrac{1}{24} ( \dfrac{a_{0}}{Z}) \int_{0}^{+inf} \rho^{5}e^{-\rho}\]
\[5! \dfrac{1}{24} (\dfrac{a_{0}}{Z})\]
\[5 (\dfrac{a_{0}}{Z})\]
a.) He+ (Z=2),
\[\langle r\rangle _{2s} = 6 \dfrac{a_{0}}{2}\]
\[\langle r\rangle _{2s}=3a_{0}\]
\[\langle r\rangle _{2p} = 5 (\dfrac{a_{0}}{2})\]
\[\langle r\rangle _{2p}=\dfrac{5}{2}a_{0}\]
b.) Be3+ (Z=4),
\[\langle r\rangle _{2s} = 6 \dfrac{a_{0}}{4}\]
\[\langle r\rangle _{2s}= \dfrac{3}{2}a_{0}\]
\[\langle r\rangle _{2p} = 5 (\dfrac{a_{0}}{4})\]
\[\langle r\rangle _{2p}=\dfrac{5}{4}a_{0}\]
Q11.10
What is the expectation value for the radius between an orbital electron and its nucleus for the 1s orbital in (a) H and (b) \(Be^{3+}\)
S11.10
To solve \(\langle R|r|R\rangle\), we use the radial function for hydrogenic species \(R_{1,0}(r)\) and see that the integral becomes
\[\int R^2r^3dr = 4\left(\dfrac{Z}{a_0}\right)^3\int r^3e^{\dfrac{-2Zr}{a_0}}dr\]
By the equation sheet the solution is \[ 4\left(\dfrac{Z}{a_0}\right)^3\left(\dfrac{3a_0^4}{8Z^4}\right)= \dfrac{3a_0}{2Z} \]
in (a) Z=1 so \[\langle r\rangle=\dfrac{3a_0}{2} \]
and (b) Z=4 so \[\langle r\rangle=\dfrac{3a_0}{8} \]
Q11.10
What is the average distance from an orbital electron to the nucleus for a 1s and 2p electron in (a) \[H\] and ( b)\[ Be^{+3}\]?
S11.10
\[\langle r \rangle = \langle \psi_{nlm} | r | \psi_{nlm} \rangle\tag{7}\]
where \[\psi_{nlm} = R_{nl} (r)Y_{lm}(\theta,\phi)\tag{8}\]
Part (a) for a 1s electron
\[\psi_{100} = R_{10}(r)Y_{00}(\theta,\phi)\]
\[\langle r \rangle = {\langle R_{10}(r) }{\langle Y_{00}(,\theta,\phi) }| r | R_{10}(r)\rangle{Y_{00}(,\theta,\phi) \rangle }\tag{9} \]
Y does not depend on are take out of integral
\[\langle r \rangle = \langle Y_{00}(\theta,\phi) | {Y_{00}(\theta,\phi) \rangle {\langle R_{10}(r) } | r | R_{10}(r) \rangle } \]
because of orthogonality of Y
\[\langle Y_{00}(\theta,\phi) | Y_{00}(\theta,\phi) \rangle = {1}\]
therefore
\[\langle r \rangle = {\langle R_{10}(r) } | r | {R_{10}(r) \rangle } \]
\[R_{10} = 2 \left (\dfrac{Z}{a_{0}} \right)^{\dfrac{3}{2}} e^\dfrac{-Zr}{a_{0}}\tag{10}\]
\[\langle r \rangle = \int^\infty_{-\infty} 2 \left (\dfrac{Z}{a_{0}} \right)^{\dfrac{3}{2}} e^\dfrac{-Zr}{a_{0}} r 2 \left (\dfrac{Z}{a_{0}} \right)^{\dfrac{3}{2}} e^\dfrac{-Zr}{a_{0}} r^{2} dr \]
\[= 4 \left (\dfrac{Z}{a_{0}} \right)^{3} \int^\infty_{-\infty} r^{3} e^\dfrac{-2Zr}{a_{0}} dr \]
using simiple exponential integrals from EQ sheet
\[\langle r \rangle = \dfrac{3a_{0}}{2Z} \]
for hydrogen Z =1 so
\[\langle r \rangle = \dfrac{3a_{0}}{2} \]
for a 2p electron
\[\psi_{210} = R_{21}(r)Y_{10}(\theta,\phi)\]
\[\langle r \rangle = \langle Y_{10}(\theta,\phi) | {Y_{10}(\theta,\phi) \rangle {\langle R_{21}(r) } | r | R_{21}(r) \rangle } \]
\[R_{21} = \dfrac{1}{\sqrt{3}} \left (\dfrac{Z}{2a_{0}} \right)^{\dfrac{3}{2}} \dfrac{Zr}{a_{0}} e^\dfrac{-Zr}{2a_{0}}\tag{11}\]
\[\langle r \rangle = \int^\infty_{-\infty} \dfrac{1}{\sqrt{3}} \left (\dfrac{Z}{2a_{0}} \right)^{\dfrac{3}{2}} \dfrac{Zr}{a_{0}} e^\dfrac{-Zr}{2a_{0}} r \dfrac{1}{\sqrt{3}} \left (\dfrac{Z}{2a_{0}} \right)^{\dfrac{3}{2}} \dfrac{Zr}{a_{0}} e^\dfrac{-Zr}{2a_{0}} r^{2} dr\]
\[= \dfrac{1}{24}\left (\dfrac{Z}{a_{0}} \right)^{5} \int^\infty_{-\infty} r^{5} e^\dfrac{-Zr}{a_{0}} dr \]
using EQ sheet simple exponential integrals
\[\langle r \rangle = \dfrac{5a_{0}}{Z} \]
Z = 1 for H
\[\langle r \rangle = 5a_{0} \]
Part (b) Be^3+
values of are stay but Z will change, Z = 4 for Be
1s \[\langle r \rangle = \dfrac{3a_{0}}{8} \]
2p \[\langle r \rangle = \dfrac{5a_{0}}{4} \]
Q11.10
What is the average distance from an orbital electron to the nucleus for a 2s and 2p electron in (a) He and (b) Be2+?
Q10.12
Show that \(\Psi_{100}\) and \(\Psi_{210}\) for the hydrogen atom are orthogonal.
S10.12
To be orthogonal \(\int_0^\infty \Psi_{100}\Psi_{210}\)\(d\tau = 0\) for \(\Psi_{100} = \frac{1}{\sqrt{\pi}a_0^{3/2}} e^{-r/a_0}\) and \(\Psi_{210} = \frac{1}{4\sqrt{2\pi}a_0^{3/2}}\frac{r}{a_0}e^{-r/2a_0}cos(\theta)\).
Evaluating the integral requires that we include the volume element while integrating in spherical coordinates:
\[\int_0^\infty\int_0^{2\pi}\int_0^{\pi} \Psi_{100}\Psi_{210} r^2sin(\theta) drd\phi d\theta\]
\[\Psi_{100}\Psi_{210} = \frac{re^{-3r/2a_0}}{4\pi\sqrt{2}a_0^4}cos(\theta)\]
The integral is now:
\[ \frac{1}{4\pi\sqrt{2}a_0^4}\int_0^\infty r^3e^{-3r/2a_0} dr \int_0^{2\pi} d\phi \int_0^{\pi}cos(\theta)sin(\theta) d\theta \]
\[= \frac{1}{4\pi\sqrt{2}a_0^4} \frac{1}{2(\frac{3}{2a_0})^2} (2\pi) \int_0^{\pi} 1/2 sin(2\theta) d\theta \]
\[= \frac{1}{4\pi\sqrt{2}a_0^4} \frac{1}{2(\frac{3}{2a_0})^2} (2\pi) [-1/4(cos(2\pi)-cos(0))] = 0\]
therefore the integral is 0 and the wavefunctions are orthogonal.
Q11.13
It can be shown that a linear combination of two eigenfunctions belonging to the same degenerate level is also an eigenfunction of the Hamiltonian with the same energy. In terms of mathematical formulas, if
\[\hat{H} \psi_1 = E_1 \psi_1\]
and
\[\hat{H} \psi_2 = E_1 \psi_2\]
then
\[\hat{H} (c1\psi_1 + c2\psi_2) = E_1 (c1\psi_1 + c2\psi_2).\]
The wavefunction \(c1\psi_1 + c2\psi_2\) still needs to be normalized. Find the real functions for the three 3p orbitals (Hint: since the imaginary part of the orbital wave functions is only contained in the spherical harmonics, do not expand the radial functions Rn,l).
S11.13
The real 3px and 3py orbitals are linear combinations of the \(\psi_{3,1,1}\) and \(\psi_{3,1,-1}\) wavefunctions since a linear combination will still be an eigenfunction of the Hamiltonian with the same energy and a linear combination will eliminate the imaginary terms in the spherical harmonics.
For 3px:
\[\psi_{3p_x} = c (\psi_{3,1,-1} - \psi_{3,1,1})\]
\[\psi_{3p_x} = c (R_{3,1} (\sqrt{\dfrac{3}{8\pi}} \sin(\theta) \exp(-i\phi)) - R_{3,1} (-\sqrt{\dfrac{3}{8\pi}} \sin(\theta) \exp(i\phi)))\]
\[\psi_{3p_x} = c R_{3,1}\sqrt{\dfrac{3}{8\pi}} \sin(\theta) (\exp(-i\phi) + \exp(i\phi))\]
\[\psi_{3p_x} = c R_{3,1}\sqrt{\dfrac{3}{8\pi}} \sin(\theta) (2 \cos(\phi))\]
In order to find the normalization constant \(c\), consider the integral over all space of the square of \(\psi_{3p_x}\). Because of the orthogonality of the wavefunctions, the probability will simplify to the following:
\[1 \equiv c^2 (1 - 0 + 1)\]
\[c = \sqrt{\dfrac{1}{2}}\]
\[\psi_{3p_x} = \dfrac{2}{\sqrt{2}} R_{3,1} \sqrt{\dfrac{3}{8\pi}} \sin(\theta) \cos(\phi)\]
For 3py:
\[\psi_{3p_y} = d (\psi_{3,1,-1} + \psi_{3,1,1})\]
\[\psi_{3p_y} = d (R_{3,1} (\sqrt{\dfrac{3}{8\pi}} \sin(\theta) \exp(-i\phi)) + R_{3,1} (-\sqrt{\dfrac{3}{8\pi}} \sin(\theta) \exp(i\phi)))\]
\[\psi_{3p_y} = d R_{3,1}\sqrt{\dfrac{3}{8\pi}} \sin(\theta) (\exp(-i\phi) - \exp(i\phi))\]
\[\psi_{3p_y} = -d R_{3,1}\sqrt{\dfrac{3}{8\pi}} \sin(\theta) (2 i \sin(\phi))\]
The normalization constant d is under the same constraints as the normalization constant c; however, it must also serve to eliminate the constant i from the real 3py orbital. Thus,
\[d = \dfrac{i}{\sqrt{2}}\]
\[\psi_{3p_y} = \dfrac{2}{\sqrt{2}} R_{3,1}\sqrt{\dfrac{3}{8\pi}} \sin(\theta) \sin(\phi)\]
For 3pz:
The real 3pz orbital does not have an imaginary term in its spherical harmonic, so its real orbital is simply the \(\psi_{3,1,0}\) wavefunction:
\[\psi_{3,1,0} = R_{3,1} \sqrt{\dfrac {3}{4 \pi}} \cos(\theta)\]
Q11.13
A linear combination of two eigenfunctions of the same degenerate level is also the eigenfunction of the Hamiltonian at the same energy. In mathematical terms,
\[\hat{H}\psi_1 = E_1\psi_1 and \hat{H}\psi_2 = E_2\psi_2\]
then,
\[\hat{H}(c_1\psi_1 + c_2\psi_2) = E_1(c_1\psi_1 + c_2\psi_2)\]
The wavefunction \[c_1\psi_1 + c_2\psi_2\] still needs to be normalized. Equation 11.5 gives the following expressions for 2p eigenfunctions:
\[\psi_{2p+1} = be^{-Zr/2a}r\sin\theta\exp^{i\phi}\]
\[\psi_{2p-1} = be^{-Zr/2a}r\sin\theta\exp^{-i\phi}\]
\[\psi_{2p_0} = ce^{-Zr/2a}r\cos\theta\]
Use the equations listed above to solve for the 2p orbitals listed in Table 11.1 given:
\[\exp^{i\phi} = \cos(\phi) + i\sin(\phi)\]
\[\exp^{-i\phi} = \cos(\phi) - i\sin(\phi)\]
Q11.13
Prove that if
ĤΨ1=E1Ψ1 and ĤΨ2=E1Ψ2 then Ĥ(c1Ψ1+c2Ψ2) = E1(c1Ψ1+c2Ψ2)
Q11.14
The spin functions α and β cannot be expressed in terms of spherical harmonics, but they can be expressed as column matrices:
\(α = \begin{bmatrix} 1 \\ 0\end{bmatrix}\) and \(β = \begin{bmatrix} 0 \\ 1\end{bmatrix}\)
The spin operator can be represented by the following Pauli matrix:
\[S_{z} = \dfrac{1}{2} \begin{bmatrix} 1 & 0 \\ 0 & -1\end{bmatrix}\]
Show that \(S_z α = \dfrac{1}{2}α\) and \(S_z β = -\dfrac{1}{2}β\).
S11.14
\[S_z α = \dfrac{1}{2} \begin{bmatrix} 1 & 0 \\ 0 & -1\end{bmatrix} \begin{bmatrix} 1 \\ 0\end{bmatrix} = \dfrac{1}{2} \begin{bmatrix} (1)(1) + (0)(0) \\ (0)(1) + (-1)(0)\end{bmatrix} = \dfrac{1}{2} \begin{bmatrix} 1 + 0 \\ 0 + 0\end{bmatrix} = \dfrac{1}{2} \begin{bmatrix} 1 \\ 0\end{bmatrix} = \dfrac{1}{2} α\]
\[S_z β = \dfrac{1}{2} \begin{bmatrix} 1 & 0 \\ 0 & -1\end{bmatrix} \begin{bmatrix} 0 \\ 1\end{bmatrix} = \dfrac{1}{2} \begin{bmatrix} (1)(0) + (0)(1) \\ (0)(0) + (-1)(1)\end{bmatrix} = \dfrac{1}{2} \begin{bmatrix} 0 + 0 \\ 0 - 1\end{bmatrix} = \dfrac{1}{2} \begin{bmatrix} 0 \\ -1\end{bmatrix} = -\dfrac{1}{2} \begin{bmatrix} 0 \\ 1\end{bmatrix} = -\dfrac{1}{2} β\]
Q11.14
Find the magnitude of angular momentum and the Z component of angular momentum for electrons in a hydrogen-like species with (a) quantum numbers n=1, l=0, m=0; and (b) n=2, l=0, m=0. (c) Compare your answers and explain your results.
S11.14
(a) The wave function for this problem is given by:\[\psi_{100}=R(r)_{10}Y(\theta,\phi)_{00}=2\left(\dfrac{Z}{2a_0}\right)^\dfrac{3}{2}e^\dfrac{-Zr}{a_0}\] Using that: \[\hat{L}^{2}Y_{lm}(\theta, \phi)=\hbar^{2}l(l+1)Y_{lm}(\theta,\phi),\] and \[\hat{L_z}=m\hbar\] Then \[\hat{L}^{2}=0\] and \[\hat{L_z}=0\].
(b) Given that the values for l and m are the same as above, the answers would also be the same.
(c) The reason why both answers are the same is that the operators for angular momentum only act on the angular part of the wave function. Since only the quantum number n varied between these two states, the angular momentum eigenvalues did not change.
Q11.14
Use the result of Problem 11-13 to verify the value of alpha used in Equation 11.5 and Figure 11.1.
S11.14
In Equation 11.5 and Figure 11.1 \[\alpha=0.4166\] and \[\zeta = 1.24\]. We substitute this value of \[\zeta\] into the result of Problem 11-13 and use the result of problem 11-11 for \[\alpha(\zeta = 1.00)\] to find \[\\\alpha(\zeta=1.24)=(0.27095) x (1.24)^2 = 0.4166\ \\\\\]
which is the value of \[\alpha\] used in Equation 11.5.
Q11.14
For a hydrogenlike atom, what is the magnitude of the orbital angular momentum for electrons in the 4f and 5d orbitals? How many radial and angular nodes do each of these orbitals have?
S11.14
Orbital angular momentum is quantized according to
\[L^2 = l(l + 1)\hbar^2\]
So
\[L = \sqrt{l(l + 1)}\hbar\]
Starting with the 4f orbital, \(l = 3\), so \(L\) is
\[L = \sqrt{(3)(4)}\hbar = \sqrt{12}\hbar\]
# of angular nodes equals l, a 4f orbital has 3 angular nodes
# of radial nodes \(= n-1 = 4-1 = 3\) radial nodes
Similarly for 5d
\[L = \sqrt{(2)(3)}\hbar = \sqrt{6}\hbar\]
d orbital has 2 angular nodes
#radial nodes \(= n-1 = 5-1 = 4\) radial nodes
Q11.14
For a hydrogen like atom, what is the magnitude of the orbital angular momentum and what are the possible values of \(L_z\) for the electrons in the 3p and 2f orbitals?
S11.14
\[L=h\sqrt{l(l+1)}\]
For the 3p orbital the magnitude of L is :
\[L=h\sqrt{1(1+1)}\]
\[L=h\sqrt{2}\]
And \(L_z\) for the 3P orbital is:
\[L_z=m_l h\]
\[L_z= -1, 0, 1\]
For the 2f orbital the magnitude of L is :
\[L=h\sqrt{3(3+1)}\]
\[L=h\sqrt{12}\]
And the \(L_z\) for the 2f orbital is :
\[L_z=m_l h\]
\[L_z= -3, -2, -1, 0, 1, 2, 3\]
Q11.17
For the wavefunction:
\[\psi =\begin{vmatrix} \psi _{A}(1)&\psi _{A}(2) \\\psi_{B}(1) &\psi_{B}(2) \end{vmatrix}\]
What is the effect on the wavefunction when:
- swapping rows of the matrix and
- swapping columns of the matrix.
S11.17
\[\psi =\psi_{A}(1)\psi_{B}(2)-\psi_{A}(2)\psi_{B}(1)\]
- if we swap rows: \[\psi_{RowSwap} =\psi_{A}(2)\psi_{B}(1)-\psi_{A}(1)\psi_{B}(2)=-\psi\]
- if we swap columns: \[\psi_{ColumSwap} =\psi_{A}(2)\psi_{B}(1)-\psi_{A}(1)\psi_{B}(2)=-\psi\]
Conclusion: swapping the rows or columns of a Slater determinant changes the sign of the wave function.
Q11.17
For the wavefunction
\[ \psi = \begin{vmatrix} \psi_A(1) & \psi_A(2) & \psi_A(3) \\ \psi_B(1) & \psi_B(2) & \psi_B(3) \\ \psi_C(1) & \psi_C(2) & \psi_C(3) \end{vmatrix}.\]
show that
- the interchange of two columns changes the sign of the wavefunction,
- the interchange of two rows changes the sign of the wavefunction, and
- the three electrons cannot have the same spin orbital.
S11.17
First find the determinant
\[ \psi = \psi_A(1) \; \begin{vmatrix}
\psi_B(2) & \psi_B(3) \\ \psi_C(2) & \psi_C(3)
\end{vmatrix}
- \psi_A(2) \; \begin{vmatrix}
\psi_B(1) & \psi_B(3) \\ \psi_C(1) & \psi_C(3)
\end{vmatrix}
+ \psi_A(3) \; \begin{vmatrix}
\psi_B(1) & \psi_B(2) \\ \psi_C(1) & \psi_C(2)
\end{vmatrix}\]
\[ = \psi_A(1) \; (\psi_B(2) \psi_C(3) - \psi_C(2) \psi_B(3)) - \psi_A(2) \; (\psi_B(1) \psi_C(3) - \psi_C(1) \psi_B(3)) + \psi_A(3) \; (\psi_B(1) \psi_C(2) - \psi_C(1) \psi_B(2)) \]
\[ \psi= \psi_A(1)\psi_B(2)\psi_C(3) - \psi_A(1)\psi_C(2)\psi_B(3) - \psi_A(2)\psi_B(1)\psi_C(3) + \psi_A(2)\psi_C(1)\psi_B(3) + \psi_A(3)\psi_B(1)\psi_C(2) - \psi_A(3)\psi_C(1)\psi_B(2)\tag{5}\]
a) Switch column \(1\) with column \(2\)
\[ \psi_{(a)}
= \begin{vmatrix}
\psi_A(2) & \psi_A(1) & \psi_A(3) \\ \psi_B(2) & \psi_B(1) & \psi_B(3) \\ \psi_C(2) & \psi_C(1) & \psi_C(3)
\end{vmatrix}\]
Now find the determinant
\[ \psi_{(a)} = \psi_A(2) \; \begin{vmatrix}
\psi_B(1) & \psi_B(3) \\ \psi_C(1) & \psi_C(3)
\end{vmatrix}
- \psi_A(1) \; \begin{vmatrix}
\psi_B(2) & \psi_B(3) \\ \psi_C(2) & \psi_C(3)
\end{vmatrix}
+ \psi_A(3) \; \begin{vmatrix}
\psi_B(2) & \psi_B(1) \\ \psi_C(2) & \psi_C(1)
\end{vmatrix}\]
\[ \psi_{(a)}= \psi_A(2)\psi_B(1)\psi_C(3) - \psi_A(2)\psi_C(1)\psi_B(3) - \psi_A(1)\psi_B(2)\psi_C(3) + \psi_A(1)\psi_C(2)\psi_B(3) + \psi_A(3)\psi_B(2)\psi_C(1) - \psi_A(3)\psi_C(2)\psi_B(1)\tag{6}\]
Comparing equation \((5)\) with equation \((6)\) we see that \(\psi = -\psi_{(a)}\)
b) Switch row \(2\) with row \(3\)
\[ \psi_{(b)}
= \begin{vmatrix}
\psi_A(1) & \psi_A(2) & \psi_A(3) \\ \psi_C(1) & \psi_C(2) & \psi_C(3) \\ \psi_B(1) & \psi_B(2) & \psi_B(3)
\end{vmatrix}.\]
Now find the determinant
\[ \psi_{(b)} = \psi_A(1) \; \begin{vmatrix}
\psi_C(2) & \psi_C(3) \\ \psi_B(2) & \psi_B(3)
\end{vmatrix}
- \psi_A(2) \; \begin{vmatrix}
\psi_C(1) & \psi_C(3) \\ \psi_B(1) & \psi_B(3)
\end{vmatrix}
+ \psi_A(3) \; \begin{vmatrix}
\psi_C(1) & \psi_C(2) \\ \psi_B(1) & \psi_B(2)
\end{vmatrix}\]
\[ \psi_{(b)}= \psi_A(1)\psi_C(2)\psi_B(3) - \psi_A(1)\psi_B(2)\psi_C(3) - \psi_A(2)\psi_C(1)\psi_B(3) + \psi_A(2)\psi_B(1)\psi_C(3) + \psi_A(3)\psi_C(1)\psi_B(2) - \psi_A(3)\psi_B(1)\psi_C(2)\tag{7}\]
Comparing equation \((5)\) with equation \((7)\) we see that \(\psi = -\psi_{(b)}\)
c) Replace column \(2\) with column \(1\)
\[ \psi_{(c)}
= \begin{vmatrix}
\psi_A(1) & \psi_A(1) & \psi_A(3) \\ \psi_B(1) & \psi_B(1) & \psi_B(3) \\ \psi_C(1) & \psi_C(1) & \psi_C(3)
\end{vmatrix}\]
Now find the determinant
\[ \psi_{(c)} = \psi_A(1) \; \begin{vmatrix}
\psi_B(1) & \psi_B(3) \\ \psi_C(1) & \psi_C(3)
\end{vmatrix}
- \psi_A(1) \; \begin{vmatrix}
\psi_B(1) & \psi_B(3) \\ \psi_C(1) & \psi_C(3)
\end{vmatrix}
+ \psi_A(3) \; \begin{vmatrix}
\psi_B(1) & \psi_B(1) \\ \psi_C(1) & \psi_C(1)
\end{vmatrix}\]
The first two terms are identical but opposite so they cancel one another. The third has a determinant of zero.
\[ \psi_{(c)} = 0 + \psi_A(3) \cdot (0) = 0\]
Q11.18
What are the electron configurations for the following atoms:
- Be-
- N+
- Al
S11.18
- Beryllium has 4 electrons so Be- has 5 electrons:
\[1s^{2}2s^{2}2p^{1}\] - Nitrogen has 7 electrons so N+ has 6 electrons:
\[1s^{2}2s^{2}2p^{2}\] - Aluminum has 13 electrons:
\[1s^{2}2s^{2}2p^{6}3s^{2}3p^{1}\]
Q11.18
Find the electronic configuration of the following atoms and ions:
Be2+, Ca2+,S, Cl1-, Si, Li2+
S11.18
Be2+: 1s2
Ca2+: 1s2 2s2 2p6 3s2 3p6
S: 1s2 2s2 2p6 3s2 3p4
Cl-: 1s2 2s2 2p6 3s2 3p6
Si: 1s2 2s2 2p6 3s2 3p2
Li2+: 1s1
Q11.18
What is the electron configuration for H-, Li+, O2-, F-, Na+ and Mg2+ ?
- H- : \[1s^{2}\]
- Li+: \[1s^{2} \]
- O2-: \[1s^{2} 2s^{2} 2p^{4} \]
- F-: \[1s^{2} 2s^{2} 2p^{6} \]
- Na+: \[1s^{2} 2s^{2} 2p^{6} \]
- Mg2+: \[1s^{2} 2s^{2} 2p^{6} 3s^{2} \]
Q11.18
What are the electron configurations for:
- C
- N
- Cl-
- H
- He
- Ne
S11.18
- Carbon has atomic number z=6. [C]: 1s22s22p2
- Nitrogen has atomic number z=7. [N]: 1s22s22p3
- Chlorine has atomic number z=17. [Cl]: 1s22s22p63s23p5. But Cl- has gained an electron. [Cl-]: 1s22s22p63s23p6, which is the same as that of the noble gas Argon.
- Hydrogen has atomic number z=1. [H]: 1s1
- He has atomic number z=2. [He]: 1s2
- Neon has atomic number z=10. [Ne]: 1s22s22p6
Q11.19
How many electrons can enter the following sets of atomic orbitals?
\[1s, 2s, 2p, 3s, 3p\]
S11.19
Each s orbital can hold 2 electrons, and each p orbital can hold 6.
\[1s \rightarrow 2\]
\[2s \rightarrow 2\]
\[2p \rightarrow 6\]
\[3s \rightarrow 2\]
\[3p \rightarrow 6\]
\[e^{-}_{total} = 2+2+6+2+6 = 18\]
Q11.19
How many electrons can enter the following sets of atomic orbitals: 4s, 4p, 4d, 4f, 5s, 5p?
S11.19
4s2: 2 electrons
4p6: 6 electrons
4d10: 10 electrons
4f14: 14 electrons
5s2: 2 electrons
5p6: 6 electrons
Q11.19
How many electrons can enter the following sets of atomic orbitals: 2s, 2p, 3s, 3p, 3d, 4f
S11.19
2s : 2
2p : 6
3s : 2
3p : 6
3d : 10
4f : 16
Q11.24
What is meant by the phrase "triple-zeta basis set"?
S11.24
A triple zeta basis set is one in which each atomic orbital is expressed as a sum of three Slater-type orbitals:
\[\varphi (r)=\varphi^{STO}(r,\zeta_1) + d_1\varphi^{STO} (r,\zeta_2)+d_2\varphi^{STO} (r,\zeta_3)\]
Q11.25
For a nitrogen atom with the configuration \([He]2s^22p^3\) the following term symbols are all possible \(^2D_{5/2}\) , \(^2D_{3/2}\) , \(^2P_{3/2}\) , \(^2P_{1/2}\) , \(^4S_{3/2}\) . According to Hund's rules, which is the most stable state?
S11.25
Hund's rules state:
- The state with the largest value of S is most stable and stability decreases with decreasing S
- For states with same values of S, the state with the largest value of L is the most stable.
- If states have same values of L and S then, for a subshell that is less than half filled, state with the smallest J is most stable; for subshells that are more than half filled, state with largest value of J is most stable.
The value of S is the value that Hund's rules is talking about is the value that is a superscript of the term symbol( \(^2\) in \(^2D_{5/2}\)). Based off this information, we know \(^4S_{3/2}\) is the most stable state.
Q11.25
For a beryllium atom in the configuration \(1s^22s^13s^1\) the following terms symbols are possible, \(^3S_1\) and \(^1S_0\). According to Hund's rules, which is the most stable state?
S11.25
According to the Hund's first rule that states "the state with the largest value of S is the most stable (has the lowest energy), and stability decreases with decreasing S. Knowing this, it is determined that \(^3S_1\) is the more stable state.
Q11.25
For a excited beryllium atom the configuration is (1s2)2s13s1 . The following term symbols are all possible 3S1 and 1S0. According to Hund's rules which is the most stable state?
S11.25
Since both S values are the same we look for the largers L value which in this case is 3. Thus the more stable state is 3S1 .
Q12.26
What is the value of the probability density of finding the electron at either nucleus in \(N_2^+\)? What is the value of this probability at the midpoint of the bond? Use \(R_{eq}=109.75\; pm\) and \(S=0.94\).
Q11.28
Calculate the energy of the ground state electron of \(He^+\) , relative to the same system at infinite separation.
S11.28
The energy of the electron is given by the equation \[E=\dfrac{hc}{\lambda}\]
where \(\dfrac{1}{\lambda}\) can be solved using the Rydberg formula for a hydrogenlike atom:
\[\dfrac{1}{\lambda}=RZ^2\left(\dfrac{1}{n^2_1}-\dfrac{1}{n^2_2}\right)\]
Plugging in with Z=2:
\[\dfrac{1}{\lambda}=(1.097\times10^7m^{-1})2^2\left(1-\dfrac{1}{\infty^2}\right) = 4.39\times10^7m^{-1}\]
Now solving for the energy:
\[E=(6.67\times10^{-34}J/s)(3.00\times10^8m/s)(4.39\times10^7m^{-1})=8.78\times10^{-18}J\]
Q11.28
Calculate the classical energy of an electron and proton separated by 0.0529 nm.
S11.28
\[F= \dfrac{ke·|q1|·|q2|}{r^2}\]
\[r=0.0529m = 0.0529*10^-9m\]
\[F= \dfrac{(8.99*10^9 \dfrac{N·m^2}{C^2}·(1.60*10^-19C)^2}{(0.0529m)^2}\]
\[F=8.22*10^-26 N\]
S11.28
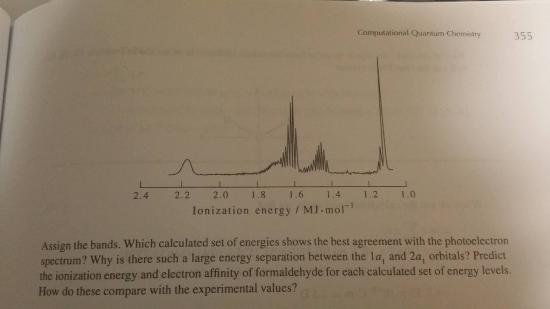
For this problem there are a total of sixteen electrons in formaldehyde. Therefore, the ground-state electronic configuration of
\[1a_{1}^{2}2a_{1}^{2}2a_{1}^{2}3a_{1}^{2}4a_{1}^{2}1b_{2}^{2}5a_{1}^{2}1b_{1}^{2}2b_{2}^{2}\]
Here, the band of approx is 1.5 MJ.mol-1 and it correspond to the 2b2
The bands 1.4 and 1.6 MJ.mol-1 arise from the ionization of electrons in the 1b1 and 5a1 and so on.
Using this facts, we now can find that
\[IE=-E_2b_2=0.4330E_h=1.136 MJ.mol^-\]
and also that
\[EA=-E_2b1=-0.1486E_h=-0.390 MJ.mol^-\]
Q11.28
Find the energy of the electron in the ground state of doubly ionized lithium and find the radius of its ground state orbit.
S11.28
Doubly Ionized Lithium
\[n=1\]
\[Z=3\]
Energy of the electron
Use Rydberg Formula in the empirical form and solve for the one over the wavelength:
\[\overline{v}= R_{H} \times Z^{2} \times (\dfrac{1}{n^{2}_1}-\dfrac{1}{n^{2}_2})\]
We want to use the ground state so we put n1 as 1 and n2 as infinity to have that term to go to zero:
\[\overline{v}=1.097 \times 10^{7}m^{-1} \times 3^{2} \times (\dfrac{1}{1^{2}_1}-\dfrac{1}{\infty^{2}_2})\]
This leaves only the Rydberg constant and Z2:
\[\overline{v}=1.097 \times 10^{7}m \times 3^{2}\]
\[\overline{v}=1.097 \times 10^{7}m \times 3^{2}\]
\[\overline{v}= 9.872 \times 10^{7}m^{-1}\]
Now that we have one over the wavelength, we can figure out the Energy:
\[E= hc\overline{v}\]
\[E= 6.626 \times 10^{-34}Js \times 2.998 \times 10^{8}ms^{-1} \times 9.872 \times 10^{7}m^{-1}\]
\[E= 1.961 \times 10^{-17}J\]
Radius of it ground state orbit
Use the quantizations of angular momentum L = r crossed p:
\[r=\dfrac {L^{2}}{Z*me^2}\]
\[L=n\hbar\]
Substitutes L into the r Equation:
\[r=\dfrac {n^{2}\hbar^{2}}{Z*me^2}\]
Bohr Radius:
\[a_{0}=\dfrac{\hbar^{2}}{me^2}\]
Substitute a0 into the r Equation:
\[r_{1}= \dfrac{n^{2}a_{0}}{Z}\]
a0 is the Bohr Radius which equals 0.0529 nm
n= 1
Z=3 because of Li
\[r_{1}= \dfrac{1^{2} \times 0.0529nm}{3}\]
\[r_{1}= 0.01763nm\]
Q11.29
For what value of n do adjacent energy levels in H have a separation of kT at 2440C where k=Boltzmann's constant (8.617*10-5eV/K)
S11.29
First convert 2440C to 517.15K
\[kT=517.15K*8.617*10^{-5}\dfrac{eV}{K}\]
For a hydrogen atom, \(E_n = \dfrac{-13.6eV}{n^2}\) Thus, \(E_{n+1} = \dfrac{-13.6eV}{(n+1)^2}\)
Putting these together,
\[\Delta E= -13.6eV(\dfrac{1}{(n+1)^2}+\dfrac{1}{n^2})=517.15K*8.617*10^{-5}\dfrac{eV}{K} \]
algebraic manipulation...
\[ -\dfrac{1}{(n+1)^2} + \dfrac{1}{n^2}= \dfrac{517.15K*8.617*10^{-5}\dfrac{eV}{K}}{13.6eV}\]
simplifying expression for n
\[\dfrac{2n+1}{n^2(n+1)^2}=.00328\]
solving emperically, we may test various n's. For n=8, we get:
\[\dfrac{2(8)+1}{8^29^2}=.00328\]
Therefore, the 8th energy level has kT separation from the 9th energy level at 244oc
Q11.29
For what value of n do adjacent energy levels in H have a separation of kT at 350K?
S11.29
\[E = 13.6\times\ (1/(n+1)^2 - 1/n^2) = kT\]
\[k = 8.62\times\ 10^-5 eV/K\]
Solve empirically in matlab:
eq = '0.03017/13.6*n^4 + 2*0.03017/13.6*n^3 + 0.03017/13.6*n^2 - 2*n - 1 = 0';
s = solve(eq);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));
disp('The third root is: '), disp(s(3));
disp('The fourth root is: '), disp(s(4));
% converting the roots to double type
disp('Numeric value of first root'), disp(double(s(1)));
disp('Numeric value of second root'), disp(double(s(2)));
disp('Numeric value of third root'), disp(double(s(3)));
disp('Numeric value of fourth root'), disp(double(s(4)));
n = 9
Q11.29
For what value of n in H is \(E_n -E_{n-3} = 84P\) at room pressure?
S11.29
First, room pressure is assumed to be \[P = 760 mmHg\]
We know that \[E_n = \dfrac{-Z^2}{2n^2}E_h\] in Atomic Units
For Hydrogen, Z=1, so \[E_n = \dfrac{-1}{2n^2}E_h\].
To find the energy values that give us the desired conditions, we construct the equation \[\dfrac{-1}{2n^2}E_h - \dfrac{-1}{2(n-3)^2}E_h = 63840\]
Next, rearrange. \[\dfrac{1}{2(n-3)^2} - \dfrac{1}{2n^2} = \dfrac{63840}{E_h}\]
Finally, we get \[0 = (127680n^2 +1)(n-3)^2-n^2\]
Using MATLAB or comparable computational software, one can plot the inverse of this solution in order to find the zeros. Thus, a zero for the polynomial would appear on the graph as a spike toward \(\infty\) or \(-\infty\). Such a plot is provided here:

Clearly, the only possible solution here is \(n=3\)
Q11.29
Calculate the translational partition function of a H2 molecule at 298 K. Assume that the volume is 3 liters.
S11.29
\[Mass of H_2= 2 x 1.008 x (1.66x10^{-27}) = 3.346x10^-27\]
\[2x3.14mkT = 2x3.14x3.346x10^{-27} x 1.3807x10^{-23}JK^{-1} x 298K\]
\[= 8.645 x 10^{-47}\]
\[ʌ = \dfrac{h}{\sqrt{2x3.14mkT}}\]
\[ʌ = \dfrac{6.626x10^{-34}}{1.0969x10^{-44}J*kg}\]
\[ʌ = 6.326x10^{-12}\]
\[q_{tr} = \dfrac{V}{ʌ^3} = \dfrac{3000 x 10^-6m^3}{6.326x10^-12m}^3 = 1.185x10^31 \]
Q11.29
For what value of n do adjacent energy levels in H have a separation of 0.008943 eV?
S11.29
The equation for the change in energy is given by:
\[\Delta E = R(\dfrac{1}{n_f^2}-\dfrac{1}{n_i^2})\tag{1}\]
\[R = 13.6eV\]
\[\Delta E = .008943eV\]
Adjacent energy levels means \[n_f = n\] and \[n_i = n+1\]. So equation (1) becomes
\[\Delta E = R(\dfrac{1}{(n)^2}-\dfrac{1}{(n+1)^2})\]
\[.008943 = 13.6(\dfrac{1}{(n)^2}-\dfrac{1}{(n+1)^2})\]
\[\dfrac{.008943}{13.6} = (\dfrac{1}{(n)^2}-\dfrac{1}{(n+1)^2})\]
Solving for n, results in \[n = 14\]
Q11.32
Calculate <r> for a 2s electron in a hydrogen atom, given
\[\int^\infty_0 e^{-ax}\, dx = \dfrac{n!}{a^{n+1}}\]
n> -1, a>0
S11.32
R20 given as:
\[ R_{2,0} = (2*(\dfrac{Z}{2ao})^{3/2}*(1 - \dfrac{Zr}{2ao})e^{\dfrac{Zr}{2a0}} \]
\[<r>=<\psi_{2,0,0} | r | \psi> = <R_{2,0}*Y_{0,0} | r | R_{2,0}*Y_{0,0}>\]
\[<R_{2,0}|r|R_{2,0}><Y_{0,0}|Y_{0,0}> = <R_{2,0}|r|R_{2,0}> * (1) \]
\[<Y_{0,0}|Y_{0,0}> =1\]
\[<R_{2,0}|r|R_{2,0}> = \int^\inf_0 (2)(\dfrac{Z}{2ao}^{3/2})(1 - \dfrac{Zr}{2ao})(e^{\dfrac{Zr}{2a0}(r)((2)(\dfrac{Z}{2ao}^{3/2})(1 - \dfrac{Zr}{2ao})(e^{\dfrac{Zr}{2a0})(r^2) \,dr \]
\[ = (4)(\dfrac{Z}{2ao})^3 \int^\inf_0 (r^3)(1- (\dfrac{Zr}{ao}) + (\dfrac{Zr}{2ao})^2)(e^{- \dfrac{Zr}{a0}}) \,dr \]
\[ = (4)(\dfrac{Z}{2ao})^3 \int^\inf_0 (r^3)(e^{- \dfrac{Zr}{ao}) - ((\dfrac{Zr^4}{ao})(e^{- \dfrac{Zr}{ao})) + (\dfrac{Z^2r^5}{4ao^2})(e^{- \dfrac{Zr}{ao}) \,dr \]
\[ \text{knowing that } \int^\inf_0 x^ne^{-ax}\, dx = \dfrac{n!}{a^{n+1}} \]
1. \[(4)(\dfrac{Z}{2ao})^3 \int^\inf_0 (r^3)(e^{- \dfrac{Zr}{ao}) \,dr \]
\[ = 4\dfrac{Z}{2ao})^3 \dfrac{6}{(\dfrac{Z}{a0})^4} = 24 \dfrac{ao}{Z} \]
2. \[- (4)(\dfrac{Z}{2ao})^3 \int^\inf_0 ((\dfrac{Zr^4}{ao})(e^{- \dfrac{Zr}{ao})) \.dr \]
\[ = -4 (\dfrac{Z}{ao})^4 (\dfrac{24}{(\dfrac{Z}{ao})^5}) = -96 \dfrac{ao}{Z} \]
3. \[ (4)(\dfrac{Z}{2ao})^3 \int^\inf_0 (\dfrac{Z^2r^5}{4ao^2})(e^{- \dfrac{Zr}{ao}) \,dr \]
\[ = 4 (\dfrac{Z}{2ao})^5 (\dfrac{120}{(\dfrac{120}{(\dfrac{Z}{ao})^6})} = 480 \dfrac{ao}{Z} \]
\[ = 24 \dfrac{ao}{Z} - 96 \dfrac{ao}{Z} + 480 \dfrac{ao}{Z} = 408 \dfrac{a0}{Z} \]
Q11.32
calculate \(\langle r \rangle\) for a 1s electron in a helium atom given
\[\int_{0}^{\infty} x^n e^{-ax}dx = \dfrac{n!}{a^{n+1}} \;\;\;\;\;\;\;\;\;\; n>-1, \; a>0 \tag{1}\]
S11.32
The hydrogenic radial function for a 1s orbital is
\[R_{1,0}(r) = 2 (\dfrac{Z}{a_0})^{3/2} e^{ -\dfrac{Zr}{a_0} } \tag{2}\]
where \(Z\) is the atomic number, \(a_0\) is the Bohr radius and \(r\) is the distance from the nucleus (radius).
We use the knowledge that
\[\langle r \rangle\ = \int_{0}^{\infty}r^3R_{1,0}^2dr \tag{3}\]
and substituting in \(R_{1,0}\) yields
\[\langle r \rangle\ = 4(\dfrac{Z}{a_0})^{3} \int_{0}^{\infty}r^3 e^{ \dfrac{-2Zr}{a_0} } dr \tag{4}\]
Using the form of the integral in equation 1 where \(n = 3\) and \(a = \dfrac{2Z}{a_0}\) the equation becomes
\[\langle r \rangle\ = 4(\dfrac{Z}{a_0})^{3} \; (3!) \; { (\dfrac{2Z}{a_0})^{-4} } \tag{5}\]
which reduces to
\[ \langle r \rangle\ = \dfrac{3}{2} \dfrac{a_0}{Z} \tag{6}\]
Substituting in the values of \(Z\) for helium and \(a_0\) yields
\[ \langle r \rangle\ = \dfrac{3}{2} \dfrac{5.29*10^{-11}m}{2} \]
which reduces to the solution
\( \langle r \rangle\ = 3.97*10^{-11}m \) or \( \langle r \rangle\ = 39.7 \; pm \)
Q11.32
Calculate \(\langle r \rangle \) for 2p in a \(He^{+}\) atom, given:
\[ \int_0^{\infty}e^{-\alpha x} dx=\dfrac {n!}{\alpha^{n+1}} \]
\[ n > -1, \alpha>0 \]
S11.32
\[ \langle r \rangle = \langle\Psi_{210} |r| \Psi_{210} \rangle \]
\[ \langle r \rangle= \langle R_{21}(r)*Y_{10}(\theta,\phi)|r| R_{21}(r)*Y_{10}(\theta,\phi)\rangle= \]
\[ \langle r \rangle= \langle Y_{10}| Y_{10} \rangle \langle R_{21}| r |R_{21} \rangle \]
Since this part is not dependent on "r":
\[\langle Y_{10}| Y_{10} \rangle=1\]
\[ \langle r \rangle= \langle R_{21}(r)|r| R_{21}(r)\rangle = \int_0^{\infty} ( \dfrac {1}{\sqrt{3}} (\dfrac{Z}{2a_0})^{3/2} \dfrac{Zr}{a_0}e^{-\dfrac{Zr}{2a_0}} )^2r*r^2dr \]
we know: Z=2
\[ \langle r \rangle= \dfrac{4}{3a_0^5} \int_0^{\infty}e^{\dfrac{-2r}{a_0}} r^5 dr \]
\[ \langle r \rangle= \dfrac{4}{3a_0^5}\dfrac{5!}{(\dfrac{2}{a_0})^6}\]
\[ \langle r \rangle=5\dfrac{a_0}{2}\]
Q11.32
Find the expectation value of r for the ground state hydrogen atom given
\[ \int _0^x e^{-ax}dx=\dfrac{n!}{a^{n+1}}\]
S11.32
<r>=∫0xΨ*(r,θ,φ)Ψ(r,θ,φ)dr
=∫0x 4/ao3e-3r/ aor3dr
= 4/ao3∫0xe-3r/ aor3dr
= 4/ao3(3ao3/8)
=3/2ao
Q11.32
Calculate: $$ \langle r \rangle \text{ for a } 2P_X \text{ electron in a hydrogen atom}\]
S11.32
\[\langle r \rangle =\int_{0}^\pi \int_{0}^{2\pi} \int_{0}^\infty \psi_{211} r \psi_{211} r^2 \sin \theta dr d \theta d \phi\]
\[=\int_{0}^\pi \int_{0}^{2\pi} \int_{0}^\infty \left(\dfrac{1}{8\pi}\right)^{\dfrac{1}{2}} \sin \theta e^{i \phi} \left(\dfrac{Z}{2a_0}\right)^{\dfrac{3}{2}} \dfrac{Zr}{a_0} e^{-\dfrac{Zr}{2a_0}} r \left(\dfrac{1}{8\pi}\right)^{\dfrac{1}{2}} \sin \theta e^{i \phi} \left(\dfrac{Z}{2a_0}\right)^{\dfrac{3}{2}} \dfrac{Zr}{a_0} e^{-\dfrac{Zr}{2a_0}} r^2 \sin \theta dr d \theta d \phi\]
\[= \left(\dfrac{1}{8\pi}\right)\left(\dfrac{Z}{2a_0}\right)^{3} \int_{0}^\pi \int_{0}^{2\pi}\int_{0}^\infty \sin \theta e^{i \phi} \dfrac{Zr}{a_0} e^{-\dfrac{Zr}{2a_0}} r \sin \theta e^{i \phi} \dfrac{Zr}{a_0} e^{-\dfrac{Zr}{2a_0}} r^2 \sin \theta dr d \theta d \phi\]
\[= \left(\dfrac{1}{8\pi}\right)\left(\dfrac{Z}{2a_0}\right)^{3} \int_{0}^\pi e^{2i \phi} d \phi \int_{0}^{2\pi} \sin \theta^3 d \theta \int_{0}^\infty \left( \dfrac{Zr}{a_0}\right)^2 e^{-\dfrac{Zr}{a_0}} r^3 dr \]
\[= \left(\dfrac{1}{8\pi}\right)\left(\dfrac{Z}{2a_0}\right)^{3}\left( \dfrac{Z}{a_0}\right)^2 \int_{0}^\pi e^{2i \phi} d \phi \int_{0}^{2\pi} \sin \theta^3 d \theta \int_{0}^\infty e^{-\dfrac{Zr}{a_0}} r^5 dr \]
\[\int_{0}^{2\pi} \sin \theta^3 d \theta=0\]
therefore:
\[\langle r \rangle = 0\]
Q11.32
Solve for the expectation value of r for an electron in a hydrogen atom in the 2p orbital
S11.32
\[\langle \psi_{210}|r|\psi_{210} \rangle=\langle R_{21}| \langle Y_{10}| r |R_{21}\rangle |Y_{10}\rangle\]
\[\langle R_{21}|r| R_{21} \rangle \langle Y_{10}| Y_{10}\rangle\]
\[\langle R_{21}|r| R_{21} \rangle\]
\[\int_{0}^\infty \dfrac{1}{3}(\dfrac{z}{2a_0})^{3}\dfrac{z^2}{a_{0}^2}(r^2)(r^2)(r)e^{(-zr)/a_0} dr\]
\[\dfrac{z^5}{24a_{0}^5}\int_{0}^\infty r^{5}e^{(-zr)/a_0} dr\]
\[\dfrac{z^5}{24a_{0}^5}(\dfrac{120a_{0}^6}{z^6})\]
\[\langle r \rangle=\dfrac{5a_0}{z}\]
z=1 for a hydrogen atom
\[\langle r \rangle=5a_0\]
Q11.34
What are the most probable positions for an electron in a \(3p_z\) orbital in hydrogen?
S11.34
Again we solve \(\langle R|r|R\rangle\), this time using \(R_{3,1}(r)\)
the integral this time is:
\[\int R^2r^3dr = \left(\dfrac{20 \sqrt{2}}{9(3a_0)^{\dfrac{5}{2}}}\right)^2\int r^4e^{\dfrac{-2r}{3a_0}}dr\]
solve the integral,
\[ \left(\dfrac{20 \sqrt{2}}{9(3a_0)^{\dfrac{4}{2}}}\right)^2\left(\dfrac{729a_0^5}{16}\right) \]
and simplify
\[\langle r\rangle=\dfrac{50a_0}{3}\]
Q11.34
What is the average value of position for the ground and first excited states of the particle-in-a-box?
S11.34
The average value of position is given by the expectation value of x,
\[\langle\ x \rangle = \int_{0}^L \psi_n x \psi_n dx\]
Substituting in the expression
\[\psi_n=\sqrt{\dfrac{2}{L}}sin(\dfrac{n\pi x}{L})\]
The expectation value becomes
\[\langle\ x \rangle = \int_{0}^L \sqrt{\dfrac{2}{L}}sin(\dfrac{n\pi x}{L}) x \sqrt{\dfrac{2}{L}}sin(\dfrac{n\pi x}{L})\]
By combining like terms and pulling out the constants,
\[\langle\ x \rangle = \dfrac{2}{L} \int_{0}^L xsin^2(\dfrac{n\pi x}{L}) dx\]
Now, using the trigonometric identity: \(sin^2(\dfrac{\alpha}{2})=\dfrac{1-cos(\alpha)}{2}\),
\[\langle\ x \rangle = \dfrac{1}{L} \int_{0}^L x(1-cos(\dfrac{2n\pi x}{L}))dx\]
Integrating, we find,
\[\langle\ x \rangle = \dfrac{1}{L}({\dfrac{x^2}{2}-\dfrac{L}{2}sin(\dfrac{2n\pi x}{L}))}_{0}^L\]
After evaluating for the given bounds, we conclude that
\[\langle\ x \rangle = \dfrac{1}{L}(\dfrac{L^2}{2}-0-(0-0))=\dfrac{L}{2}\]
Q11.34
What is the most probable position for an electron in 1s in H?
S11.34
Find the radius at which the radial distribution function of the hydrogenic 1s orbital has a maximum value by solving dP/dr = 0.
\[\dfrac{dP(r)}{dr} = 0\]
Radial distribution function for a 1s orbital is
\[P(r) = \dfrac{4Z^{3}}{a_{0}^{3}} r^{2}e^{-2Z_{r} / a_{0}}\]
Solving dP/dr=0 gives
\[\dfrac{dP(r)}{dr} =0 =\dfrac{4z^{3}}{a_{0}^{3}}(2r - \dfrac{2Zr^{2}}{a_{0}})e^{-2Zr/a_0}\]
The function is zero when the term in the parentheses is zero, which is at
\[r=\dfrac{a_{0}}{Z}\]
Most probable position for an electron in 1s in H (Z=1) is
\[a_{0}\]
Q11.34
What are the most probable positions for an electron in a 2s orbital in He^+
S11.34
We use the radial function for 2s orbital
\[R_{20}(r) = 2 \left (\dfrac{Z}{2a_{0}} \right)^{\dfrac{3}{2}} \left (1 - \dfrac {Zr}{2a_{0}} \right) e^\dfrac{-Zr}{2a_{0}}\tag{12}\]
To find the positions we must take the derivative of the radial function and set to 0
\[\dfrac{d}{dr}\left(R_{20}(r) \right) = 2 \left (\dfrac{Z}{2a_{0}} \right)^{\dfrac{3}{2}} \left (\dfrac {-Z}{2a_{0}} \right) e^\dfrac{-Zr}{2a_{0}} + 2 \left (\dfrac{Z}{2a_{0}} \right)^{\dfrac{3}{2}} \left (1 - \dfrac {Zr}{2a_{0}} \right) \left (\dfrac {-Z}{2a_{0}} \right) e^\dfrac{-Zr}{2a_{0}} = 0\]
\[1 + \left (1 - \dfrac{ therefore \[ r = \dfrac{4a_{0}}{Z}\] for He Z = 2 \[ r = 2a_{0}\]Q11.36
Show that Ψ1S and Ψ2p are orthogonal for the Hydrogen atom.
S11.36
\[Ψ_{n,l,m}=R_{n,l}(r)Y_{l,m}(ϑ,φ)\]
\[Ψ_{1,0,0} = \dfrac{1}{\sqrt{π}}(\dfrac{Z}{a_0})^{\dfrac{3}{2}}e^{\dfrac{-Zr}{a_0}}\]
\[Ψ_{2,1,0} = \sqrt{\dfrac{3}{4π}}cos(ϑ)\dfrac{1}{\sqrt{3}}(\dfrac{Z}{2a_0})\dfrac{Zr}{a_0}e^{\dfrac{-Zr}{2a_0}} \]
\[<Ψ_{1,0,0}|Ψ_{2,1,0}> = <R_{1,0}(r)Y_{0,0}(ϑ,φ)|R_{2,1}(r)Y_{1,0}(ϑ,φ)> \]
\[<Ψ_{1,0,0}|Ψ_{2,1,0}> = <R_{1,0}(r)|R_{2,1}(r)><Y_{0,0}(ϑ,φ)|Y_{1,0}(ϑ,φ)> \]
If we observe just the theta components of the wave functions, cos(ϑ), and ignore constants, we only have to evaluate the integral over this component to see that these functions are orthogonal.
\[ \int_0^π cos(ϑ)sin(ϑ) dϑ \]
from formula sheet
\[ = \dfrac{1}{2ϑ}sin^2(ϑ) |_0^π \]
\[ = 0 \]
Q11.36
Show that \[\psi_1s\] and \[\psi_2s\] are orthogonal for the He atom.
Q11.42
Derive the determinantal wave function , including normalization constant, for a lithium atom. Then, evaluate the determinant and show that it is nonzero.
S11.42
Genrally, a normalized N-electron determinantal wave function can be represented as (adapted from "Quantum States of Atoms and Molecules" by David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski)
\[ \Psi(\mathbf{r}_1, \mathbf{r}_2, \ldots, \mathbf{r}_N)=\dfrac{1}{\sqrt{N!}} \left| \begin{matrix} \chi_1(\mathbf{r}_1) & \chi_2(\mathbf{r}_1) & \cdots & \chi_N(\mathbf{r}_1) \\ \chi_1(\mathbf{r}_2) & \chi_2(\mathbf{r}_2) & \cdots & \chi_N(\mathbf{r}_2) \\ \vdots & \vdots & \ddots & \vdots \\ \varphi_1(\mathbf{r}_N) & \chi_2(\mathbf{r}_N) & \cdots & \chi_N(\mathbf{r}_N) \end{matrix} \right|\]
Plugging in the 3 electrons of lithium gives us
\[ \Psi_{Li}(\mathbf{r}_1, \mathbf{r}_2, \mathbf{r}_3)=\dfrac{1}{\sqrt{3!}} \left| \begin{matrix} 1s\alpha (1) & 1s\beta(1) & 2s\alpha (1) \\ 1s\alpha (2) & 1s\beta(2) & 2s\alpha (2) \\ 1s\alpha (3) & 1s\beta(3) & 2s\alpha (3) \end{matrix} \right| \]
patrickJMT has a great video on youtube for finding the determinant of a 3x3 matrix. The first step leads to
\[\dfrac{1}{\sqrt{3!}} (1s\alpha (1)\left| \begin{matrix} 1s\beta (2) & 2s\alpha (2) \\ 1s\beta (3) & 2s\alpha (3) \end{matrix} \right| -1s\beta (1) \left| \begin{matrix} 1s\alpha (2) & 2s\alpha (2) \\ 1s\alpha (3) & 2s\alpha (3) \end{matrix} \right| + 2s\alpha (1) \left| \begin{matrix} 1s\alpha (2) & 1s\beta (2) \\ 1s\alpha (3) & 1s\beta (3) \end{matrix} \right|) \]
Next, take the determinant of each 2x2 matrix
\[\dfrac{1}{\sqrt{3!}} (1s\alpha (1) (1s\beta (2) 2s\alpha (3) - 1s\beta (3) 2s\alpha (2)) - 1s\beta(1) (1s\alpha(2) 2s\alpha (2) - 1s\alpha(3) 2s\alpha (2)) + 2s\alpha (1) (1s\alpha(2) 1s\beta (3) - 1s\beta (2) 1s\alpha (3)))\]
Factor the wave equation into the product of a spatial part and a spin part on your own. The fact that is determinant is nonzero means this wave equation satisfies the Pauli-exclusion principle.
Q11.42
Prove that the Slater determinant for a Li atom is antisymmetric; i.e. when the electrons are interchanged, it changes signs.
S11.42
The Slater determinant for Li is given by:
\[\psi=\dfrac{1}{\sqrt{3!}}\left|\begin{array}{ccc} 1s\alpha(1) & 1s\beta (1) & 2s\alpha(1) \\ 1s\alpha(2) & 1s\beta(2) & 2s\alpha(2) \\ 1s\alpha(3) & 1s\beta(3) & 2s\alpha(3)\end{array}\right|\]
Ignoring the normalization constant, we have
\[1s\alpha(1)1s\beta(2)2s\alpha(3) -1s\alpha(1)1s\beta(3)2s\alpha(2) -1s\alpha(2)1s\beta(1)2s\alpha(3)\] \[+1s\alpha(2)1s\beta(3)2s\alpha(1) +1s\alpha(3)1s\beta(1)2s\alpha(2) -1s\alpha(3)1s\beta(2)2s\alpha(1)\]
Interchanging electrons 1 and 2, we find
\[1s\alpha(2)1s\beta(1)2s\alpha(3) -1s\alpha(2)1s\beta(3)2s\alpha(1) -1s\alpha(1)1s\beta(2)2s\alpha(3)\] \[+1s\alpha(1)1s\beta(3)2s\alpha(2) +1s\alpha(3)1s\beta(2)2s\alpha(1) -1s\alpha(3)1s\beta(1)2s\alpha(2)\]
Which may also be written as
\[1s\alpha(1)1s\beta(2)2s\alpha(3) +1s\alpha(1)1s\beta(3)2s\alpha(2) +1s\alpha(2)1s\beta(1)2s\alpha(3)\] \[-1s\alpha(2)1s\beta(3)2s\alpha(1) -1s\alpha(3)1s\beta(1)2s\alpha(2) +1s\alpha(3)1s\beta(2)2s\alpha(1)\]
Or
\[-(1s\alpha(1)1s\beta(2)2s\alpha(3) -1s\alpha(1)1s\beta(3)2s\alpha(2) -1s\alpha(2)1s\beta(1)2s\alpha(3)\] \[+1s\alpha(2)1s\beta(3)2s\alpha(1) +1s\alpha(3)1s\beta(1)2s\alpha(2) -1s\alpha(3)1s\beta(2)2s\alpha(1))\]
Q11.42
Show that the following wavefuntions for the Helium atom is anti symmetric to the interchange of the two electrons.
\[\Psi_(1,2) =\left| \begin{matrix} 1s\alpha (1) & 1s\beta (1) \\ 1s\alpha (2) & 1s\beta (2) \end{matrix} \right| \]
S11.42
First we start off with taking the determinant of the matrix for \phi
\[\Psi_(1,2)=1s\alpha(1)1s\beta(2) - 1s\beta(1)1s\alpha(2)\]
Then we interchange the columns and rows of the matrix
\[\Psi_(2,1) =\left| \begin{matrix} 1s\alpha (2) & 1s\beta (2) \\ 1s\alpha (1) & 1s\beta (1) \end{matrix} \right| \]
Then the determinant becomes:
\[\Psi _(2,1)=1s\alpha(2)1s\beta(1) - 1s\beta(2)1s\alpha(1)\]
if we add the two determinants together we get
\[\Psi_(1,2) +\Psi _(2,1)=1s\alpha(1)1s\beta(2) - 1s\beta(1)1s\alpha(2) + 1s\alpha(2)1s\beta(1) - 1s\beta(2)1s\alpha(1)=0\]
\[\Psi_(1,2) +\Psi _(2,1)=1s\alpha(1)1s\beta(2) + 1s\alpha(2)1s\beta(1) - 1s\beta(1)1s\alpha(2) - 1s\beta(2)1s\alpha(1)=0\]
\[\Psi_(1,2) +\phi _(2,1) = 0\]
\[\Psi_(2,1) =-\phi _(1,1) \]
Q11.44
Write the electronic configuration of the following atoms and ions:
- C
- Na+
- Ar
- O2-
S11.44
- [C]: \(1s^22s^22p^2\)
- [Na+ ]: \(1s^22s^22p^6\) , (Na becomes Na+ by losing its 3s valence electron)
- [Ar]: \(1s^22s^22p^63s^23p^6\)
- [O2-]: \(1s^22s^22p^6\), (O becomes O2- by gaining 2 electrons into its 2p orbital)
Q11.44
Give the electronic configurations for the ground states of the first 20 electrons in the periodic table.
S11.44
| Hydrogen | \(1s^1\) |
|---|---|
| Helium | \(1s^2\) |
| Lithium | \(1s^2 2s^1\) |
| Beryllium | \(1s^2 2s^2\) |
| Boron | \(1s^2 2s^2 2p^1\) |
| Carbon | \(1s^2 2s^2 2p^2\) |
| Nitrogen | \(1s^2 2s^2 2p^3\) |
| Oxygen | \(1s^2 2s^2 2p^4\) |
| Fluorine | \(1s^2 2s^2 2p^5\) |
| Neon | \(1s^2 2s^2 2p^6\) |
| Sodium | \(1s^2 2s^2 2p^6 3s^1\) |
| Magnesium | \(1s^2 2s^2 2p^6 3s^2\) |
| Aluminum | \(1s^2 2s^2 2p^6 3s^2 3p^1\) |
| Silicon | \(1s^2 2s^2 2p^6 3s^2 3p^2\) |
| Phosphorus | \(1s^2 2s^2 2p^6 3s^2 3p^3\) |
| Sulfur | \(1s^2 2s^2 2p^6 3s^2 3p^4\) |
| Chlorine | \(1s^2 2s^2 2p^6 3s^2 3p^5\) |
| Argon | \(1s^2 2s^2 2p^6 3s^2 3p^6\) |
| Potassium | \(1s^2 2s^2 2p^6 3s^2 3p^6 4s^1\) |
| Calcium | \(1s^2 2s^2 2p^6 3s^2 3p^6 4s^2\) |
Q11.44
Write out the first ionization electronic configurations for atoms from \(Z=1\) to \(Z=11\) (i.e \(H^{+}, He^{+}\)). Explain which shell the electron falls out of and why.
S11.44
\(H^{+} =\) No electrons \(He^{+} = 1s^{1}\) \(Li^{+} = 1s^{2}\) \(Be^{+} = 1s^{2}2s^{1}\) \(B^{+} = 1s^{2}2s^{2}\) \(C^{+} = 1s^{2}2s^{2}2p^{1}\) \(N^{+} = 1s^{2}2s^{2}2p^{2}\) \(O^{+} = 1s^{2}2s^{2}2p^{3}\) \(F^{+} = 1s^{2}2s^{2}2p^{4}\) \(Ne^{+} = 1s^{2}2s^{2}2p^{5}\) \(Na^{+} = 1s^{2}2s^{2}2p^{6}\) Electrons are always ionized from the outermost (valence) shell. This is because they are the furthest from the nucleus and therefore require the least amount of energy to "pull off".Q10.45
If we use \(\Psi\) as a trial function for the Hamiltonian \(\hat{H}|\), Where \(\Psi = \dfrac{(\phi_0 +a\phi_1)}{\sqrt{(1+a^2)}}\)
And \(\phi_0\)and \(\phi_1\) are the two lowest eigenfunctions with eigenvalues E0 and E1(with E1>E0), show that the variational method yields a=0.
S10.45
The variational method when applied to a trial function is as follows:
\[\left \langle E_{trial} \right \rangle = \dfrac{ \langle \psi _{trial}| \hat {H} | \psi _{trial} \rangle}{\langle \psi _{trial} | \psi _{trial} \rangle} = \dfrac {\int \psi _{trial} ^* \hat {H} \psi _{trial} d \tau}{\int \psi _{trial} ^* \psi _{trial} d\tau } \]
We also know that
\[\left \langle E_{trial} \right \rangle = \dfrac{ \langle \psi _{trial}| \hat {H} | \psi _{trial} \rangle}{\langle \psi _{trial} | \psi _{trial} \rangle}\ge E_0\]
\[\langle \psi _{trial} | \psi _{trial} \rangle = \int \dfrac{(\phi_0 +a\phi_1)}{\sqrt{(1+a^2)}} * \dfrac{(\phi_0 +a\phi_1)}{\sqrt{(1+a^2)}}d\tau\]
\[= \int\dfrac{\phi_0^2}{1+a^2}d\tau+\int\dfrac{2a\phi_1\phi_0}{1+a^2}d\tau +\int\dfrac{a^2\phi_1^2}{1+a^2}d\tau\]
Assuming \(\psi_1\) and \(\psi_0\) normalized:
\[\langle \psi _{trial} | \psi _{trial} \rangle = \dfrac{1+a^2}{1+a^2}+\dfrac{2a}{1+a^2}\int\phi_1\phi_0=1\]
Provided with the respective eigenvalues of the eigenfunctions:
\[\left \langle E_{trial} \right \rangle = \langle \psi _{trial}| \hat {H} | \psi _{trial} \rangle = \dfrac {E_0+aE_1}{\sqrt{1+a^2}}\]
And minimizing for our parameter a s.t. \(\dfrac {E_0+aE_1}{\sqrt{1+a^2}}\ge E_0\) we find that a=0.
Q10.47
For what value of n do adjacent energy levels in H have a separation of kT at room temperature?
S10.47
k = Boltzmann's constant (8.617 x 10-5 eV/K)
Room temperature is 300 K
\[kT = (300 \space K)(8.617 \times 10^{-5}\dfrac{eV}{K})\]
For a hydrogen atom, \(E_n = \dfrac{-13.6eV}{n^2}\) and \(E_{n+1} = \dfrac{-13.6eV}{(n+1)^2}\)
Putting these together,
\[\Delta E= -13.6eV(\dfrac{1}{(n + 1)^2}+\dfrac{1}{n^2}) = (300 \space K)(8.617 \times 10^{-5}\dfrac{eV}{K})\]
\[ -\dfrac{1}{(n + 1)^2} + \dfrac{1}{n^2} = \dfrac{(300 \space K)(8.617 \times 10^{-5}\dfrac{eV}{K})}{13.6eV}\]
\[\dfrac{2n + 1}{n^2(n + 1)^2} = .00190\]
For n = 10, we get:
\[\dfrac{2(10) + 1}{(10^2)(11^2)} = .00174\]
Thus, the 10th energy level has kT separation from the 11th energy level at 300 K.