Analysis of the IR Spectrum of Carbon Monoxide
- Page ID
- 96247
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Goal: The infrared (IR) spectrum of carbon monoxide is analyzed in order to determine the rotational constant (B) of this diatomic.
- Prerequisites: A basic knowledge of IR spectroscopy and the quantum mechanical harmonic oscillator and rigid rotor models.
- Resources you will need: This exercise should be carried out within a quantitative analysis software environment that is capable data manipulation and can generate a best-fit line for an x-y data set. You will also be graphing the data along with the fitted function.
The infrared (IR) spectrum of a simple heteronuclear diatomic reveals a series of regularly spaced peaks. A typical spectrum is illustrated in Figure \(\PageIndex{1}\).
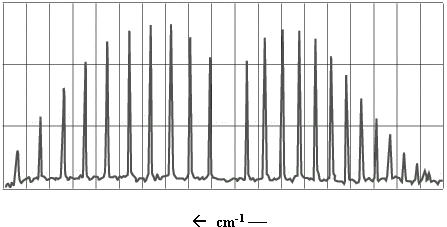
Figure \(\PageIndex{1}\): IR spectrum of \(CO\).
This exercise will involve an analysis of the IR spectrum of carbon monoxide, which looks much like the spectrum in Figure \(\PageIndex{1}\). To understand the information contained in the \(\ce{CO}\) spectrum, we must take into account the vibrational and rotational energy levels of the molecule.
To a first approximation, the vibration of the carbon-oxygen bond is well described by the harmonic oscillator model. The energy levels of a harmonic oscillator are given by
\[E_{v} = \omega \left( v+ \dfrac{1}{2} \right) \label{1}\]
where \(v\) is the vibrational quantum number (0, 1, 2 ….) and \(ω\) is the harmonic frequency of oscillator. This frequency can in turn be calculated from
\[\omega = \sqrt{\dfrac{k}{\mu}} \label{2}\]
where \(k\) is the spring constant of the bond and \(μ\) is the reduced mass of the diatomic,
\[\mu = \dfrac{m_Cm_O}{m_C+m_O} \label{3}\]
The rotational energy levels of \(\ce{CO}\) can be described using the rigid rotor model, which has energies
\[ E_J = BJ (J+1) \label{4}\]
where \(J\) is the rotational quantum number (0, 1, 2, 3, …) and \(B\) is the rotational constant,
\[ B =\dfrac{\hbar^2}{2I} = \dfrac{\hbar^2}{2 \mu R^2} \label{5}\]
In Equation \ref{5}, \(I\) represents the moment of inertia and \(R\) the equilibrium bond distance.
The combined rotational-vibrational energy (ro-vibrational energy) can be obtained by adding Equations \ref{1} and \ref{4} which yields
\[E_{v,J} = \omega \left( v+ \dfrac{1}{2} \right) + BJ (J+1) \label{6}\]
When a diatomic absorbs a photon of IR light, there can be a simultaneous change in vibrational and rotational quantum number. However, not all transitions are permitted. The selection rules that apply to this system tell us that only transitions whereby \(Δυ = ±1\) and \(ΔJ = ±1\) are allowed. At room temperature, nearly all of the \(\ce{CO}\) molecules reside in their ground vibrational state (\(v = 0\)), so the vibrational transition that predominates is the \(v = 0 \to 1\) transition. But a wide range of rotational states are thermally occupied within the ground vibrational state, so several \(ΔJ = ±1\) rotational transitions can coincide with the \(v = 0 \to 1\) jump.
Figure \(\PageIndex{2}\) shows a number of ro-vibrational energy levels for \(\ce{CO}\). By convention, ground state parameters are identified with a double prime, “, and excited state parameters with a single prime,’. Of the transitions that can occur between the \(v”\) and \(v’\) level, some will involve a decrease in rotational quantum number (\(ΔJ = -1\)) and the others will involve an increase (\(ΔJ = +1\)). The peaks in the IR spectrum that arise from \(ΔJ = -1\) transitions are called P-branch transitions and the \(ΔJ = +1\) transitions are called R-branch transitions (three possible P-branch and three possible R-branch transitions are shown in Figure \(\PageIndex{2}\)).
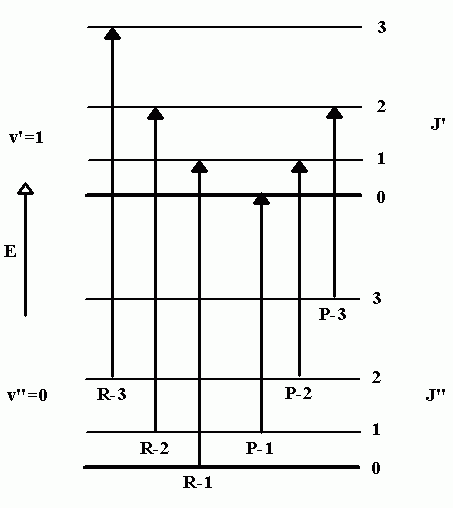
Figure \(\PageIndex{2}\): Ro-vibrational transitions.
Referring back to Figure \(\PageIndex{1}\), the P-branch transitions give rise to a series of peaks that appear at lower wave numbers. The R-branch series appears at higher wave numbers. There appears to be a peak missing between these two series; no peak appears here because \(ΔJ = 0\) transitions are not allowed.
In this assignment, you will be given the peak positions of several \(v = 0 \to 1\) transitions in the carbon monoxide IR spectrum with a goal of determining the rotational constant of this diatomic. To accomplish this, you will first identify pairs of transition peaks that terminate in the same \(J’\) level (one peak each from the \(P\) and \(R\) branches). Once we have identified the appropriate pairs, we will subtract their wave number values to obtain an energy difference. As an example, consider the \(R-1\) and \(P-2\) transitions in Figure \(\PageIndex{2}\), which both terminate in the \(J’=1\) level. By subtracting the wavenumber values for this pair of transitions we obtain the energy difference between the \(J”=0\) and \(J”=2\) levels (in the ground vibrational state). This can be represented symbolically by writing
\[ \Delta E_{J''=1} = \tilde{\nu}_{P-2} - \tilde{\nu}_{R-1} = E_{0,2} - E_{0,0} \label{7}\]
In a similar fashion, the subtraction of successive pairs of peak positions will yield the energy difference between the \(J”=1\) and \(J”=3\) levels, and the \(J”=2\) and \(J”=4\) levels, which can be represented by writing
\[ \Delta E_{J''=2} = \tilde{\nu}_{P-3} - \tilde{\nu}_{R-2} = E_{0,3} - E_{0,1} \nonumber\]
\[ \Delta E_{J''=3} = \tilde{\nu}_{P-4} - \tilde{\nu}_{R-3} = E_{0,4} - E_{0,2} \nonumber\]
or more generally as
\[ \Delta E_{J''=3} = E_{0,J''+1} - E_{0,J"-1} \label{8}\]
Using Equation \ref{6}, we can derive a theoretical expression for this energy difference as follows:
\[ \Delta E_{J''} = \left[ \omega \left(\dfrac{1}{2} \right) + B (J''+1)(J''+2) \right] - \left[ \omega \left(\dfrac{1}{2} \right) + B (J''-1)(J'') \right] \nonumber\]
which simplifies to
\[ \Delta E_{J''} = 2B (2J +1 ) \label{9}\]
According to Equation \ref{9}, a plot of successive energy differences versus \((2J"+1)\) is linear and the slope equals \(2B\).
Experimental Data
Click on the following link and save the numerical information to an appropriate folder. The data corresponds to the fundamental gas phase IR spectrum of \(\ce{^{12}C^{16}O}\); the absorption peak wave number positions are listed from smallest to largest in one long column (the P-branch peaks are listed first, the word ‘center’ indicates the relative placement of the missing peak, and then the R-branch peaks are listed). All wave number values have been corrected for the index of refraction in air (yielding peak positions that would be observed in a vacuum). The data was obtained from Rao, K.N. and Mathews, C.W., editors, Molecular Spectroscopy: Modern Research, Academic Press, New York, 1972.
Wave number positions for the \(v = 0 \to 1\) infrared transitions in \(\ce{^{12}C^{16}O}\)
Exercise
- Import the data into an appropriate quantitative analysis software package. For convenience, separate the data into two new columns (or two arrays); one array will contain R-branch peak positions starting with the peak closest to the center of the spectrum (start the array with the peak position originating from \(J” = 0\)) and the other array will contain P-branch peak positions starting with the peak closest to the center of the spectrum (start the array with the peak position originating from \(J” = 1\)).
- Which two peaks (one from the P-branch and one from the R-branch) correspond to transitions that terminate in the \(J’=1\) level? What two peaks terminate in the \(J’=2\) level? The \(J’=3\) level?
- Once you recognize the pattern of successive peak pairs that terminate in a particular \(J’\) level, subtract the successive wave number positions so that you generate two new columns of data corresponding to \(ΔE\), \(J\), and \((2J"+1)\). Plot this data along with a best fit line, and determine the rotational constant for this diatomic. Look up an appropriate literature value for \(B\) and calculate the percent difference.
- Using your result, calculate the moment of inertia (\(I\)) and the equilibrium bond length (\(R\)) of \(\ce{CO}\).
- MORE CHALLENGING: The analysis described here yields the rotational constant for the ground vibrational state. When \(\ce{CO}\) transitions to the \(v = 1\) state, the equilibrium bond length becomes slightly longer and the rotational constant becomes correspondingly smaller, as dictated by Equation \ref{5}. In other words, the rotational constant varies with vibrational quantum number (these rotational constants are distinguished from one another by including the vibrational quantum number as a subscript; \(B_0\), \(B_1\), \(B_2\) …). How would you alter the analysis described here to obtain \(B_1\) (HINT: you will need to find pairs of transitions that originate from the same rotational level in the ground vibrational state)? Carry out this analysis and report the new rotational constant. Based on your result, how much does the equilibrium bond length differ between the \(v = 0\) and \(v = 1\) levels?


