Adsorption Isotherms - Methylene Blue on Activated Carbon

Learning Objectives

Goal: Data is presented for the adsorption of methylene blue onto activated carbon from aqueous solution. The results are analyzed within the context of two common adsorption models; the Langmuir and Freundlich adsorption isotherms.

Prerequisites: An introductory knowledge of dynamic equilibria, rate laws, and using adsorption spectroscopy data to determine solute concentrations.

Resources you will need: This exercise should be carried out within a software environment that is capable of data manipulation and which can generate a best-fit line for an x-y data set. You will also be graphing the data along with the fitted function.

Chemical reactions are often classified as being either homogeneous or heterogeneous. In the later case, the reactants and catalyst (if any) exist in different phases, and consequently the reaction occurs at the phase boundary. Many important industrial reactions fall into this category, including the classic Haber ammonia synthesis, whereby nitrogen and hydrogen gas are catalytically combined on a metal surface at elevated pressures. Modeling the adsorption of various solutes on a solid substrate remains an active area of research which is advancing our understanding of catalytic processes and many biological reactions.

One of the initial models for the adsorption of a species onto a simple surface was put forth by Irving Langmuir in 1916. Langmuir assumed that a surface consists of a given number of equivalent sites where a species can physically or chemically stick. Physical adsorption through van der Waals interactions is called physisorption, whereas chemical adsorption through the formation of a covalent bond is called chemisorption. It is important to realize that the processes of adsorption and the opposite process (desorption) is dynamic; a rate law can be written for each process, and when the rates become equal an equilibrium state will exist characterized by a constant fractional coverage of the original sites. Letting \(x_o\) represent the total concentration of available sites on a given amount of fresh solid substrate, we can define a fractional coverage (\(θ\)) as

\[\theta = \dfrac{x}{x_o} \label{1}\]

where x is the concentration of occupied sites. The rate of adsorption va will be proportional to the concentration of gas or liquid (c) above the surface and the fraction of the surface that is not covered \((1-θ)\), yielding a rate equation

\[v_a = k_Ac(1-\theta) \label{2}\]

where \(k_a\) is the rate constant for adsorption. The rate of desorption is simply proportional to the fraction of the surface that is already occupied, so the rate equation is

\[v_d = k_d \theta \label{3}\]

and kd is the rate constant for desorption. Setting Equations \ref{2} and \ref{3} equal yields an equilibrium statement that can be written as

\[\dfrac{\theta }{1-\theta} = \dfrac{k_a}{k_d} c \label{4}\]

The ratio of rate constants in Equation \ref{4} is equal to an equilibrium constant

\[K = \dfrac{k_a}{k_d}.\]

Upon substitution and further rearrangement, the fractional coverage is given by

\[ \theta = \dfrac{Kc}{1+Kc} \label{5}\]

Equation \ref{5} is plotted in Figure \(\PageIndex{1}\) for an arbitrary value of \(K\), illustrating how the surface sites becomes saturated as the concentration rises. The magnitude of K quantifies the relative affinity that a given solute has for surface adsorption. Like all equilibrium constants, K is temperature dependent. A plot like the one shown in figure 1 is often called a Langmuir absorption isotherm.

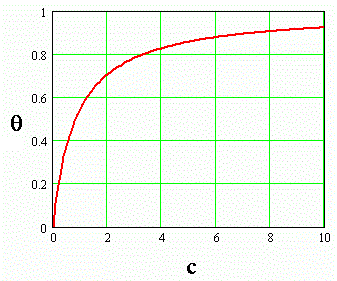
Figure \(\PageIndex{1}\)

For many studies, it is more convenient to substitute \(x/x_o\) back in place of \(θ\) and rearrange Equation \ref{5} into the following form for the concentration of occupied sites;

\[ x = \dfrac{x_oKc}{1+Kc} \label{6}\]

In this case, \(K\) and \(x_o\) are both constants for a system. They are normally evaluated by writing Equation \ref{6} in the reciprocal form

\[ \dfrac{1}{x} = \left( \dfrac{1}{x_mK} \right) \dfrac{1}{c} + \dfrac{1}{x_m} \label{7}\]

\(x\) is measured experimentally at different values of \(c\) and a plot of \(1/x\) versus \(1/c\) yields linear data where the slope and intercept can be used to evaluate the constants \(K\) and \(x_o\).

How well does the Langmuir model work? In cases where there is negligible intermolecular interaction between adsorbed solute particles and where only one monolayer of solute can potentially adsorb, the Langmuir model works quite well. As such, the model can be thought of as a limiting law (much like the ideal gas equation). Several more sophisticated models have since been developed that account for deviations from Langmuir adsorption behavior. One such model is called the Freundlich isotherm (proposed by Herbert Max Finlay Freundlich, 1880-1941) and is described by the equation

\[ x =k c^{1/n} \label{8}\]

where \(k\) and \(n\) are empirical constants (and x and c have the same meaning as before). While originally proposed by Freundlich as an empirical law, Equation \ref{8} can be arrived at theoretically by taking into account repulsive interactions between adsorbed solute particles and also accounting for surface heterogeneities. To determine the constants \(k\) and \(n\), Equation \ref{8} is rearranged into the form

\[ \log_{10} x = \dfrac{1}{n} \log_{10} c + log_{10} k \label{9}\]

A plot of \(\log_{10} x\) versus \(\log_{10} c\) should be linear and the slope and intercept yield the empirical constants.

In the exercise below, you will analyze data corresponding to the adsorption of dye called methylene blue onto activated carbon from solution using both the Langmuir and Freundlich adsorption isotherm models.

Experimental Data

The following data are based upon measurements described in J.H. Potgieter, Journal of Chemical Education, 68, 349 (1991). For each trial, a given amount of activated carbon (indicated below in milligrams) was measured into a small flask. 100 mL of a 25 mg/L methylene blue stock solution was then added to each flask. The flasks were agitated on a mechanical shaker for 72 hours at 25 °C, at which point the solutions were filtered and the amount of methylene blue remaining in solution was measured by spectrophotometry at 630 nm. The absorbance readings are reported in the table below relative to the absorbance of the methylene blue stock solution (which had an absorbance Ao).

Trial	Activated Carbon (mg)	Absorbance ratio of methylene blue (A/Ao)
1	1	0.796
2	5	0.432
3	10	0.168
4	12.5	0.140
5	25	0.040
6	30	0.028
7	100	0.008

Exercise

1. To test the Langmuir and Freundlich adsorption models, you will need to calculate x and c for each trial. Noting that 100 mL of a 25 mg/L methylene blue (MB) stock solution was added to each flask, calculate the initial mass of MB before adsorption (in mg units). Then use the absorbance ratios (A/Ao) to determine the mass of MB in solution after adsorption (in mg units), the mass of MB adsorbed onto the carbon (in mg units), and finally the concentration of MB in solution after adsorption, c, in units of mg/L.
2. Generate two plots of the data: 1/x versus 1/c (to test the Langmuir model) and log x versus log c (to test the Freundlich model) and include a best-fit line along with the original data. In each case, report the constants xm and K, and n and k, from your fitting parameters. Comment about the agreement between the original data and each model.
3. Absorbents, like activated carbon, are materials that have an extraordinarily large 'specific' surface area, S. This parameter can be approximated from the Langmuir constant xm using the expression S = xm•N• a, where N is Avogadro's number and a is the area of the absorbing molecule. Assuming that methylene blue has an area of 120 Å2, calculate the specific surface area of the activated carbon (in units of m2/gram). Compare this area to a regulation soccer field (100 m x 70 m).