13.4: Chapter 13 Problems
- Page ID
- 23764
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)An underlined problem number or problem-part letter indicates that the numerical answer appears in Appendix I.
13.1 Consider a single-phase system that is a gaseous mixture of \(\mathrm{N}_{2}, \mathrm{H}_{2}\), and \(\mathrm{NH}_{3}\). For each of the following cases, find the number of degrees of freedom and give an example of the independent intensive variables that could be used to specify the equilibrium state, apart from the total amount of gas.
(a) There is no reaction.
(b) The reaction \(\mathrm{N}_{2}(\mathrm{~g})+3 \mathrm{H}_{2}(\mathrm{~g}) \rightarrow 2 \mathrm{NH}_{3}(\mathrm{~g})\) is at equilibrium.
(c) The reaction is at equilibrium and the system is prepared from \(\mathrm{NH}_{3}\) only.
13.2 How many components has a mixture of water and deuterium oxide in which the equilibrium \(\mathrm{H}_{2} \mathrm{O}+\mathrm{D}_{2} \mathrm{O} \rightleftharpoons 2\) HDO exists?
13.3 Consider a system containing only \(\mathrm{NH}_{4} \mathrm{Cl}(\mathrm{s}), \mathrm{NH}_{3}(\mathrm{~g})\), and \(\mathrm{HCl}(\mathrm{g}) .\) Assume that the equilibrium \(\mathrm{NH}_{4} \mathrm{Cl}(\mathrm{s}) \rightleftharpoons \mathrm{NH}_{3}(\mathrm{~g})+\mathrm{HCl}(\mathrm{g})\) exists.
(a) Suppose you prepare the system by placing solid \(\mathrm{NH}_{4} \mathrm{Cl}\) in an evacuated flask and heating to \(400 \mathrm{~K}\). Use the phase rule to decide whether you can vary the pressure while both phases remain in equilibrium at \(400 \mathrm{~K}\).
(b) According to the phase rule, if the system is not prepared as described in part (a) could you vary the pressure while both phases remain in equilibrium at \(400 \mathrm{~K}\) ? Explain.
(c) Rationalize your conclusions for these two cases on the basis of the thermodynamic equilibrium constant. Assume that the gas phase is an ideal gas mixture and use the approximate expression \(K=p_{\mathrm{NH}_{3}} p_{\mathrm{HCl}} /\left(p^{\circ}\right)^{2}\).
13.4 Consider the lime-kiln process \(\mathrm{CaCO}_{3}(\mathrm{~s}) \rightarrow \mathrm{CaO}(\mathrm{s})+\mathrm{CO}_{2}(\mathrm{~g})\). Find the number of intensive variables that can be varied independently in the equilibrium system under the following conditions:
(a) The system is prepared by placing calcium carbonate, calcium oxide, and carbon dioxide in a container.
(b) The system is prepared from calcium carbonate only.
(c) The temperature is fixed at \(1000 \mathrm{~K}\).
13.5 What are the values of \(C\) and \(F\) in systems consisting of solid \(\mathrm{AgCl}\) in equilibrium with an aqueous phase containing \(\mathrm{H}_{2} \mathrm{O}, \mathrm{Ag}^{+}(\mathrm{aq}), \mathrm{Cl}^{-}(\mathrm{aq}), \mathrm{Na}^{+}(\mathrm{aq})\), and \(\mathrm{NO}_{3}^{-}(\mathrm{aq})\) prepared in the following ways? Give examples of intensive variables that could be varied independently.
(a) The system is prepared by equilibrating excess solid \(\mathrm{AgCl}\) with an aqueous solution of \(\mathrm{NaNO}_{3}\).
(b) The system is prepared by mixing aqueous solutions of \(\mathrm{AgNO}_{3}\) and \(\mathrm{NaCl}\) in arbitrary proportions; some solid \(\mathrm{AgCl}\) forms by precipitation.
13.6 How many degrees of freedom has a system consisting of solid \(\mathrm{NaCl}\) in equilibrium with an aqueous phase containing \(\mathrm{H}_{2} \mathrm{O}, \mathrm{Na}^{+}(\mathrm{aq}), \mathrm{Cl}^{-}(\mathrm{aq}), \mathrm{H}^{+}(\mathrm{aq})\), and \(\mathrm{OH}^{-}(\mathrm{aq})\) ? Would it be possible to independently vary \(T, p\), and \(m_{\mathrm{OH}^{-}}\)? If so, explain how you could do this.
13.7 Consult the phase diagram shown in Fig. \(13.4\) on page 430. Suppose the system contains \(36.0 \mathrm{~g}\) (2.00 mol) \(\mathrm{H}_{2} \mathrm{O}\) and \(58.4 \mathrm{~g}\) (1.00 mol) \(\mathrm{NaCl}\) at \(25^{\circ} \mathrm{C}\) and 1 bar.
(a) Describe the phases present in the equilibrium system and their masses.
(b) Describe the changes that occur at constant pressure if the system is placed in thermal contact with a heat reservoir at \(-30^{\circ} \mathrm{C}\).
(c) Describe the changes that occur if the temperature is raised from \(25^{\circ} \mathrm{C}\) to \(120^{\circ} \mathrm{C}\) at constant pressure.
(d) Describe the system after \(200 \mathrm{~g} \mathrm{H}_{2} \mathrm{O}\) is added at \(25^{\circ} \mathrm{C}\).
Table 13.1 Aqueous solubilities of sodium sulfate decahydrate and anhydrous sodium sulfate \({ }^{a}\)
\begin{tabular}{lccc}
\hline \(\mathrm{Na}_{2} \mathrm{SO}_{4} \cdot 10 \mathrm{H}_{2} \mathrm{O}\) & & \multicolumn{2}{c}{\(\mathrm{Na}_{2} \mathrm{SO}_{4}\)} \\
\cline { 1 - 2 } \cline { 5 }\(t /{ }^{\circ} \mathrm{C}\) & \(x_{\mathrm{B}}\) & \(t /{ }^{\circ} \mathrm{C}\) & \(x_{\mathrm{B}}\) \\
\hline 10 & \(0.011\) & 40 & \(0.058\) \\
15 & \(0.016\) & 50 & \(0.056\) \\
20 & \(0.024\) & & \\
25 & \(0.034\) & & \\
30 & \(0.048\) & & \\
\hline\({ }^{a}\) Ref. [59], p. 179-180. & & \\
& & &
\end{tabular}
13.8 Use the following information to draw a temperature-composition phase diagram for the binary system of \(\mathrm{H}_{2} \mathrm{O}(\mathrm{A})\) and \(\mathrm{Na}_{2} \mathrm{SO}_{4}(\mathrm{~B})\) at \(p=1\) bar, confining \(t\) to the range \(-20\) to \(50^{\circ} \mathrm{C}\) and \(z_{\mathrm{B}}\) to the range \(0-0.2\). The solid decahydrate, \(\mathrm{Na}_{2} \mathrm{SO}_{4} \cdot 10 \mathrm{H}_{2} \mathrm{O}\), is stable below \(32.4^{\circ} \mathrm{C}\). The anhydrous salt, \(\mathrm{Na}_{2} \mathrm{SO}_{4}\), is stable above this temperature. There is a peritectic point for these two solids and the solution at \(x_{\mathrm{B}}=0.059\) and \(t=32.4^{\circ} \mathrm{C}\). There is a eutectic point for ice, \(\mathrm{Na}_{2} \mathrm{SO}_{4} \cdot 10 \mathrm{H}_{2} \mathrm{O}\), and the solution at \(x_{\mathrm{B}}=0.006\) and \(t=-1.3^{\circ} \mathrm{C}\). Table \(13.1\) gives the temperature dependence of the solubilities of the ionic solids.
Table 13.2 Data for Problem 13.9. Temperatures of saturated solutions of aqueous iron(III) chloride at \(p=\) 1 bar (\left(\mathrm{A}=\mathrm{FeCl}_{3}, \mathrm{~B}=\mathrm{H}_{2} \mathrm{O}\right)^{a}\)
\begin{tabular}{crcccr}
\hline\(x_{\mathrm{A}}\) & \(t /{ }^{\circ} \mathrm{C}\) & \(x_{\mathrm{A}}\) & \(t /{ }^{\circ} \mathrm{C}\) & \(x_{\mathrm{A}}\) & \(t /{ }^{\circ} \mathrm{C}\) \\
\hline \(0.000\) & \(0.0\) & \(0.119\) & \(35.0\) & \(0.286\) & \(56.0\) \\
\(0.020\) & \(-10.0\) & \(0.143\) & \(37.0\) & \(0.289\) & \(55.0\) \\
\(0.032\) & \(-20.5\) & \(0.157\) & \(36.0\) & \(0.293\) & \(60.0\) \\
\(0.037\) & \(-27.5\) & \(0.173\) & \(33.0\) & \(0.301\) & \(69.0\) \\
\(0.045\) & \(-40.0\) & \(0.183\) & \(30.0\) & \(0.318\) & \(72.5\) \\
\(0.052\) & \(-55.0\) & \(0.195\) & \(27.4\) & \(0.333\) & \(73.5\) \\
\(0.053\) & \(-41.0\) & \(0.213\) & \(32.0\) & \(0.343\) & \(72.5\) \\
\(0.056\) & \(-27.0\) & \(0.222\) & \(32.5\) & \(0.358\) & \(70.0\) \\
\(0.076\) & \(0.0\) & \(0.232\) & \(30.0\) & \(0.369\) & \(66.0\) \\
\(0.083\) & \(10.0\) & \(0.238\) & \(35.0\) & \(0.369\) & \(80.0\) \\
\(0.093\) & \(20.0\) & \(0.259\) & \(50.0\) & \(0.373\) & \(100.0\) \\
\(0.106\) & \(30.0\) & \(0.277\) & \(55.0\) & & \\
\hline
\end{tabular}
\({ }^{a}\) Data from Ref. [59], page \(193 .\)
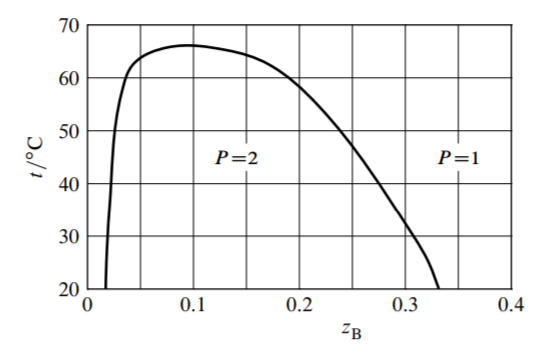
13.9 Iron(III) chloride forms various solid hydrates, all of which melt congruently. Table \(13.2\) on the preceding page lists the temperatures \(t\) of aqueous solutions of various compositions that are saturated with respect to a solid phase.
(a) Use these data to construct a \(t-z_{\mathrm{B}}\) phase diagram for the binary system of \(\mathrm{FeCl}_{3}\) (A) and \(\mathrm{H}_{2} \mathrm{O}\) (B). Identify the formula and melting point of each hydrate. Hint: derive a formula for the mole ratio \(n_{\mathrm{B}} / n_{\mathrm{A}}\) as a function of \(x_{\mathrm{A}}\) in a binary mixture.
(b) For the following conditions, determine the phase or phases present at equilibrium and the composition of each.
1. \(t=-70.0^{\circ} \mathrm{C}\) and \(z_{\mathrm{A}}=0.100\)
2. \(t=50.0^{\circ} \mathrm{C}\) and \(z_{\mathrm{A}}=0.275\)
\(\overline
Callstack:
at (Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/DeVoes_Thermodynamics_and_Chemistry/13:_The_Phase_Rule_and_Phase_Diagrams/13.04:_Chapter_13_Problems), /content/body/p[31]/span, line 1, column 2
13.10 Figure \(13.19\) is a temperature-composition phase diagram for the binary system of water (A) and phenol (B) at 1 bar. These liquids are partially miscible below \(67^{\circ} \mathrm{C}\). Phenol is more dense than water, so the layer with the higher mole fraction of phenol is the bottom layer. Suppose you place \(4.0 \mathrm{~mol}\) of \(\mathrm{H}_{2} \mathrm{O}\) and \(1.0 \mathrm{~mol}\) of phenol in a beaker at \(30^{\circ} \mathrm{C}\) and gently stir to allow the layers to equilibrate.
(a) What are the compositions of the equilibrated top and bottom layers?
(b) Find the amount of each component in the bottom layer.
(c) As you gradually stir more phenol into the beaker, maintaining the temperature at \(30^{\circ} \mathrm{C}\), what changes occur in the volumes and compositions of the two layers? Assuming that one layer eventually disappears, what additional amount of phenol is needed to cause this to happen?
13.11 The standard boiling point of propane is \(-41.8{ }^{\circ} \mathrm{C}\) and that of \(n\)-butane is \(-0.2{ }^{\circ} \mathrm{C}\). Table \(13.3\) on the next page lists vapor pressure data for the pure liquids. Assume that the liquid mixtures obey Raoult's law.
(a) Calculate the compositions, \(x_{\mathrm{A}}\), of the liquid mixtures with boiling points of \(-10.0^{\circ} \mathrm{C}\), \(-20.0^{\circ} \mathrm{C}\), and \(-30.0^{\circ} \mathrm{C}\) at a pressure of \(1 \mathrm{bar}\).
(b) Calculate the compositions, \(y_{\mathrm{A}}\), of the equilibrium vapor at these three temperatures.
Table \(13.3\) Saturation vapor pressures of propane (A) and \(n\)-butane (B)
\begin{tabular}{ccc}
\hline\(t /{ }^{\circ} \mathrm{C}\) & \(p_{\mathrm{A}}^{*} /\) bar & \(p_{\mathrm{B}}^{*} / \mathrm{bar}\) \\
\hline\(-10.0\) & \(3.360\) & \(0.678\) \\
\(-20.0\) & \(2.380\) & \(0.441\) \\
\(-30.0\) & \(1.633\) & \(0.275\) \\
\hline
\end{tabular}
(c) Plot the temperature-composition phase diagram at \(p=1\) bar using these data, and label the areas appropriately.
(d) Suppose a system containing \(10.0 \mathrm{~mol}\) propane and \(10.0 \mathrm{~mol} n\)-butane is brought to a pressure of 1 bar and a temperature of \(-25^{\circ} \mathrm{C}\). From your phase diagram, estimate the compositions and amounts of both phases.
Table 13.4 Liquid and gas compositions in the two-phase system of 2-propanol (A) and benzene at \(45^{\circ} \mathrm{C}^{a}\)
\begin{tabular}{llcccc}
\hline\(x_{\mathrm{A}}\) & \(y_{\mathrm{A}}\) & \(p / \mathrm{kPa}\) & \(x_{\mathrm{A}}\) & \(y_{\mathrm{A}}\) & \(p / \mathrm{kPa}\) \\
\hline 0 & 0 & \(29.89\) & \(0.5504\) & \(0.3692\) & \(35.32\) \\
\(0.0472\) & \(0.1467\) & \(33.66\) & \(0.6198\) & \(0.3951\) & \(34.58\) \\
\(0.0980\) & \(0.2066\) & \(35.21\) & \(0.7096\) & \(0.4378\) & \(33.02\) \\
\(0.2047\) & \(0.2663\) & \(36.27\) & \(0.8073\) & \(0.5107\) & \(30.28\) \\
\(0.2960\) & \(0.2953\) & \(36.45\) & \(0.9120\) & \(0.6658\) & \(25.24\) \\
\(0.3862\) & \(0.3211\) & \(36.29\) & \(0.9655\) & \(0.8252\) & \(21.30\) \\
\(0.4753\) & \(0.3463\) & \(35.93\) & \(1.0000\) & \(1.0000\) & \(18.14\) \\
\hline
\end{tabular}
\({ }^{a}\) Ref. [24].
13.12 Use the data in Table \(13.4\) to draw a pressure-composition phase diagram for the 2-propanolbenzene system at \(45^{\circ} \mathrm{C}\). Label the axes and each area.
Table 13.5 Liquid and gas compositions in the twophase system of acetone (A) and chloroform at \(35.2{ }^{\circ} \mathrm{C}\)
\begin{tabular}{lllccc}
\hline\(x_{\mathrm{A}}\) & \(y_{\mathrm{A}}\) & \(p / \mathrm{kPa}\) & \(x_{\mathrm{A}}\) & \(y_{\mathrm{A}}\) & \(p / \mathrm{kPa}\) \\
\hline 0 & 0 & \(39.08\) & \(0.634\) & \(0.727\) & \(36.29\) \\
\(0.083\) & \(0.046\) & \(37.34\) & \(0.703\) & \(0.806\) & \(38.09\) \\
\(0.200\) & \(0.143\) & \(34.92\) & \(0.815\) & \(0.896\) & \(40.97\) \\
\(0.337\) & \(0.317\) & \(33.22\) & \(0.877\) & \(0.936\) & \(42.62\) \\
\(0.413\) & \(0.437\) & \(33.12\) & \(0.941\) & \(0.972\) & \(44.32\) \\
\(0.486\) & \(0.534\) & \(33.70\) & \(1.000\) & \(1.000\) & \(45.93\) \\
\(0.577\) & \(0.662\) & \(35.09\) & & & \\
\hline
\end{tabular}
\({ }^{a}\) Ref. [179], p. \(286 .\)


