13.2: Phase Diagrams- Binary Systems
- Page ID
- 20628
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
\( \newcommand{\tx}[1]{\text{#1}} % text in math mode\)
\( \newcommand{\subs}[1]{_{\text{#1}}} % subscript text\)
\( \newcommand{\sups}[1]{^{\text{#1}}} % superscript text\)
\( \newcommand{\st}{^\circ} % standard state symbol\)
\( \newcommand{\id}{^{\text{id}}} % ideal\)
\( \newcommand{\rf}{^{\text{ref}}} % reference state\)
\( \newcommand{\units}[1]{\mbox{$\thinspace$#1}}\)
\( \newcommand{\K}{\units{K}} % kelvins\)
\( \newcommand{\degC}{^\circ\text{C}} % degrees Celsius\)
\( \newcommand{\br}{\units{bar}} % bar (\bar is already defined)\)
\( \newcommand{\Pa}{\units{Pa}}\)
\( \newcommand{\mol}{\units{mol}} % mole\)
\( \newcommand{\V}{\units{V}} % volts\)
\( \newcommand{\timesten}[1]{\mbox{$\,\times\,10^{#1}$}}\)
\( \newcommand{\per}{^{-1}} % minus one power\)
\( \newcommand{\m}{_{\text{m}}} % subscript m for molar quantity\)
\( \newcommand{\CVm}{C_{V,\text{m}}} % molar heat capacity at const.V\)
\( \newcommand{\Cpm}{C_{p,\text{m}}} % molar heat capacity at const.p\)
\( \newcommand{\kT}{\kappa_T} % isothermal compressibility\)
\( \newcommand{\A}{_{\text{A}}} % subscript A for solvent or state A\)
\( \newcommand{\B}{_{\text{B}}} % subscript B for solute or state B\)
\( \newcommand{\bd}{_{\text{b}}} % subscript b for boundary or boiling point\)
\( \newcommand{\C}{_{\text{C}}} % subscript C\)
\( \newcommand{\f}{_{\text{f}}} % subscript f for freezing point\)
\( \newcommand{\mA}{_{\text{m},\text{A}}} % subscript m,A (m=molar)\)
\( \newcommand{\mB}{_{\text{m},\text{B}}} % subscript m,B (m=molar)\)
\( \newcommand{\mi}{_{\text{m},i}} % subscript m,i (m=molar)\)
\( \newcommand{\fA}{_{\text{f},\text{A}}} % subscript f,A (for fr. pt.)\)
\( \newcommand{\fB}{_{\text{f},\text{B}}} % subscript f,B (for fr. pt.)\)
\( \newcommand{\xbB}{_{x,\text{B}}} % x basis, B\)
\( \newcommand{\xbC}{_{x,\text{C}}} % x basis, C\)
\( \newcommand{\cbB}{_{c,\text{B}}} % c basis, B\)
\( \newcommand{\mbB}{_{m,\text{B}}} % m basis, B\)
\( \newcommand{\kHi}{k_{\text{H},i}} % Henry's law constant, x basis, i\)
\( \newcommand{\kHB}{k_{\text{H,B}}} % Henry's law constant, x basis, B\)
\( \newcommand{\arrow}{\,\rightarrow\,} % right arrow with extra spaces\)
\( \newcommand{\arrows}{\,\rightleftharpoons\,} % double arrows with extra spaces\)
\( \newcommand{\ra}{\rightarrow} % right arrow (can be used in text mode)\)
\( \newcommand{\eq}{\subs{eq}} % equilibrium state\)
\( \newcommand{\onehalf}{\textstyle\frac{1}{2}\D} % small 1/2 for display equation\)
\( \newcommand{\sys}{\subs{sys}} % system property\)
\( \newcommand{\sur}{\sups{sur}} % surroundings\)
\( \renewcommand{\in}{\sups{int}} % internal\)
\( \newcommand{\lab}{\subs{lab}} % lab frame\)
\( \newcommand{\cm}{\subs{cm}} % center of mass\)
\( \newcommand{\rev}{\subs{rev}} % reversible\)
\( \newcommand{\irr}{\subs{irr}} % irreversible\)
\( \newcommand{\fric}{\subs{fric}} % friction\)
\( \newcommand{\diss}{\subs{diss}} % dissipation\)
\( \newcommand{\el}{\subs{el}} % electrical\)
\( \newcommand{\cell}{\subs{cell}} % cell\)
\( \newcommand{\As}{A\subs{s}} % surface area\)
\( \newcommand{\E}{^\mathsf{E}} % excess quantity (superscript)\)
\( \newcommand{\allni}{\{n_i \}} % set of all n_i\)
\( \newcommand{\sol}{\hspace{-.1em}\tx{(sol)}}\)
\( \newcommand{\solmB}{\tx{(sol,$\,$$m\B$)}}\)
\( \newcommand{\dil}{\tx{(dil)}}\)
\( \newcommand{\sln}{\tx{(sln)}}\)
\( \newcommand{\mix}{\tx{(mix)}}\)
\( \newcommand{\rxn}{\tx{(rxn)}}\)
\( \newcommand{\expt}{\tx{(expt)}}\)
\( \newcommand{\solid}{\tx{(s)}}\)
\( \newcommand{\liquid}{\tx{(l)}}\)
\( \newcommand{\gas}{\tx{(g)}}\)
\( \newcommand{\pha}{\alpha} % phase alpha\)
\( \newcommand{\phb}{\beta} % phase beta\)
\( \newcommand{\phg}{\gamma} % phase gamma\)
\( \newcommand{\aph}{^{\alpha}} % alpha phase superscript\)
\( \newcommand{\bph}{^{\beta}} % beta phase superscript\)
\( \newcommand{\gph}{^{\gamma}} % gamma phase superscript\)
\( \newcommand{\aphp}{^{\alpha'}} % alpha prime phase superscript\)
\( \newcommand{\bphp}{^{\beta'}} % beta prime phase superscript\)
\( \newcommand{\gphp}{^{\gamma'}} % gamma prime phase superscript\)
\( \newcommand{\apht}{\small\aph} % alpha phase tiny superscript\)
\( \newcommand{\bpht}{\small\bph} % beta phase tiny superscript\)
\( \newcommand{\gpht}{\small\gph} % gamma phase tiny superscript\)
\( \newcommand{\upOmega}{\Omega}\)
\( \newcommand{\dif}{\mathop{}\!\mathrm{d}} % roman d in math mode, preceded by space\)
\( \newcommand{\Dif}{\mathop{}\!\mathrm{D}} % roman D in math mode, preceded by space\)
\( \newcommand{\df}{\dif\hspace{0.05em} f} % df\)
\(\newcommand{\dBar}{\mathop{}\!\mathrm{d}\hspace-.3em\raise1.05ex{\Rule{.8ex}{.125ex}{0ex}}} % inexact differential \)
\( \newcommand{\dq}{\dBar q} % heat differential\)
\( \newcommand{\dw}{\dBar w} % work differential\)
\( \newcommand{\dQ}{\dBar Q} % infinitesimal charge\)
\( \newcommand{\dx}{\dif\hspace{0.05em} x} % dx\)
\( \newcommand{\dt}{\dif\hspace{0.05em} t} % dt\)
\( \newcommand{\difp}{\dif\hspace{0.05em} p} % dp\)
\( \newcommand{\Del}{\Delta}\)
\( \newcommand{\Delsub}[1]{\Delta_{\text{#1}}}\)
\( \newcommand{\pd}[3]{(\partial #1 / \partial #2 )_{#3}} % \pd{}{}{} - partial derivative, one line\)
\( \newcommand{\Pd}[3]{\left( \dfrac {\partial #1} {\partial #2}\right)_{#3}} % Pd{}{}{} - Partial derivative, built-up\)
\( \newcommand{\bpd}[3]{[ \partial #1 / \partial #2 ]_{#3}}\)
\( \newcommand{\bPd}[3]{\left[ \dfrac {\partial #1} {\partial #2}\right]_{#3}}\)
\( \newcommand{\dotprod}{\small\bullet}\)
\( \newcommand{\fug}{f} % fugacity\)
\( \newcommand{\g}{\gamma} % solute activity coefficient, or gamma in general\)
\( \newcommand{\G}{\varGamma} % activity coefficient of a reference state (pressure factor)\)
\( \newcommand{\ecp}{\widetilde{\mu}} % electrochemical or total potential\)
\( \newcommand{\Eeq}{E\subs{cell, eq}} % equilibrium cell potential\)
\( \newcommand{\Ej}{E\subs{j}} % liquid junction potential\)
\( \newcommand{\mue}{\mu\subs{e}} % electron chemical potential\)
\( \newcommand{\defn}{\,\stackrel{\mathrm{def}}{=}\,} % "equal by definition" symbol\)
\( \newcommand{\D}{\displaystyle} % for a line in built-up\)
\( \newcommand{\s}{\smash[b]} % use in equations with conditions of validity\)
\( \newcommand{\cond}[1]{\\[-2.5pt]{}\tag*{#1}}\)
\( \newcommand{\nextcond}[1]{\\[-5pt]{}\tag*{#1}}\)
\( \newcommand{\R}{8.3145\units{J$\,$K$\per\,$mol$\per$}} % gas constant value\)
\( \newcommand{\Rsix}{8.31447\units{J$\,$K$\per\,$mol$\per$}} % gas constant value - 6 sig figs\)
\( \newcommand{\jn}{\hspace3pt\lower.3ex{\Rule{.6pt}{2ex}{0ex}}\hspace3pt} \)
\( \newcommand{\ljn}{\hspace3pt\lower.3ex{\Rule{.6pt}{.5ex}{0ex}}\hspace-.6pt\raise.45ex{\Rule{.6pt}{.5ex}{0ex}}\hspace-.6pt\raise1.2ex{\Rule{.6pt}{.5ex}{0ex}} \hspace3pt} \)
\( \newcommand{\lljn}{\hspace3pt\lower.3ex{\Rule{.6pt}{.5ex}{0ex}}\hspace-.6pt\raise.45ex{\Rule{.6pt}{.5ex}{0ex}}\hspace-.6pt\raise1.2ex{\Rule{.6pt}{.5ex}{0ex}}\hspace1.4pt\lower.3ex{\Rule{.6pt}{.5ex}{0ex}}\hspace-.6pt\raise.45ex{\Rule{.6pt}{.5ex}{0ex}}\hspace-.6pt\raise1.2ex{\Rule{.6pt}{.5ex}{0ex}}\hspace3pt} \)
As explained in Sec. 8.2, a phase diagram is a kind of two-dimensional map that shows which phase or phases are stable under a given set of conditions. This section discusses some common kinds of binary systems, and Sec. 13.3 will describe some interesting ternary systems.
13.2.1 Generalities
A binary system has two components; \(C\) equals \(2\), and the number of degrees of freedom is \(F=4-P\). There must be at least one phase, so the maximum possible value of \(F\) is 3. Since \(F\) cannot be negative, the equilibrium system can have no more than four phases.
We can independently vary the temperature, pressure, and composition of the system as a whole. Instead of using these variables as the coordinates of a three-dimensional phase diagram, we usually draw a two-dimensional phase diagram that is either a temperature–composition diagram at a fixed pressure or a pressure–composition diagram at a fixed temperature. The position of the system point on one of these diagrams then corresponds to a definite temperature, pressure, and overall composition. The composition variable usually varies along the horizontal axis and can be the mole fraction, mass fraction, or mass percent of one of the components, as will presently be illustrated by various examples.
The way in which we interpret a two-dimensional phase diagram to obtain the compositions of individual phases depends on the number of phases present in the system.
- If the system point falls within a one-phase area of the phase diagram, the composition variable is the composition of that single phase. There are three degrees of freedom. On the phase diagram, the value of either \(T\) or \(p\) has been fixed, so there are two other independent intensive variables. For example, on a temperature–composition phase diagram, the pressure is fixed and the temperature and composition can be changed independently within the boundaries of the one-phase area of the diagram.
- If the system point is in a two-phase area of the phase diagram, we draw a horizontal tie line of constant temperature (on a temperature–composition phase diagram) or constant pressure (on a pressure–composition phase diagram). The lever rule applies. The position of the point at each end of the tie line, at the boundary of the two-phase area, gives the value of the composition variable of one of the phases and also the physical state of this phase: either the state of an adjacent one-phase area, or the state of a phase of fixed composition when the boundary is a vertical line. Thus, a boundary that separates a two-phase area for phases \(\pha\) and \(\phb\) from a one-phase area for phase \(\pha\) is a curve that describes the composition of phase \(\pha\) as a function of \(T\) or \(p\) when it is in equilibrium with phase \(\phb\). The curve is called a solidus, liquidus, or vaporus depending on whether phase \(\pha\) is a solid, liquid, or gas.
- A binary system with three phases has only one degree of freedom and cannot be represented by an area on a two-dimensional phase diagram. Instead, there is a horizontal boundary line between areas, with a special point along the line at the junction of several areas. The compositions of the three phases are given by the positions of this point and the points at the two ends of the line. The position of the system point on this line does not uniquely specify the relative amounts in the three phases.
The examples that follow show some of the simpler kinds of phase diagrams known for binary systems.
13.2.2 Solid–liquid systems
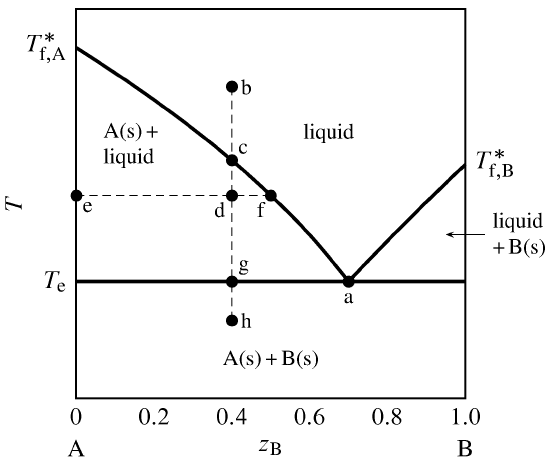
Figure 13.1 Temperature–composition phase diagram for a binary system exhibiting a eutectic point.
Figure 13.1 is a temperature–composition phase diagram at a fixed pressure. The composition variable \(z\B\) is the mole fraction of component B in the system as a whole. The phases shown are a binary liquid mixture of A and B, pure solid A, and pure solid B.
The one-phase liquid area is bounded by two curves, which we can think of either as freezing-point curves for the liquid or as solubility curves for the solids. These curves comprise the liquidus. As the mole fraction of either component in the liquid phase decreases from unity, the freezing point decreases. The curves meet at point a, which is a eutectic point. At this point, both solid A and solid B can coexist in equilibrium with a binary liquid mixture. The composition at this point is the eutectic composition, and the temperature here (denoted \(T\subs{e}\)) is the eutectic temperature. (“Eutectic” comes from the Greek for easy melting.) \(T\subs{e}\) is the lowest temperature for the given pressure at which the liquid phase is stable.
Suppose we combine \(0.60\mol\) A and \(0.40\mol\) B (\(z\B=0.40\)) and adjust the temperature so as to put the system point at b. This point is in the one-phase liquid area, so the equilibrium system at this temperature has a single liquid phase. If we now place the system in thermal contact with a cold reservoir, heat is transferred out of the system and the system point moves down along the isopleth (path of constant overall composition) b–h. The cooling rate depends on the temperature gradient at the system boundary and the system’s heat capacity.
At point c on the isopleth, the system point reaches the boundary of the one-phase area and is about to enter the two-phase area labeled A(s) + liquid. At this point in the cooling process, the liquid is saturated with respect to solid A, and solid A is about to freeze out from the liquid. There is an abrupt decrease (break) in the cooling rate at this point, because the freezing process involves an extra enthalpy decrease.
At the still lower temperature at point d, the system point is within the two-phase solid–liquid area. The tie line through this point is line e–f. The compositions of the two phases are given by the values of \(z\B\) at the ends of the tie line: \(x\B\sups{s}=0\) for the solid and \(x\B\sups{l} =0.50\) for the liquid. From the general lever rule (Eq. 8.2.8), the ratio of the amounts in these phases is \begin{equation} \frac{n\sups{l} }{n\sups{s}} = \frac{z\B-x\B\sups{s}}{x\B\sups{l} -z\B} = \frac{0.40-0}{0.50-0.40} = 4.0 \tag{13.2.1} \end{equation} Since the total amount is \(n\sups{s}+n\sups{l} =1.00\mol\), the amounts of the two phases must be \(n\sups{s}=0.20\mol\) and \(n\sups{l} =0.80\mol\).
When the system point reaches the eutectic temperature at point g, cooling halts until all of the liquid freezes. Solid B freezes out as well as solid A. During this eutectic halt, there are at first three phases: liquid with the eutectic composition, solid A, and solid B. As heat continues to be withdrawn from the system, the amount of liquid decreases and the amounts of the solids increase until finally only \(0.60\mol\) of solid A and \(0.40\mol\) of solid B are present. The temperature then begins to decrease again and the system point enters the two-phase area for solid A and solid B; tie lines in this area extend from \(z\B{=}0\) to \(z\B{=}1\).
Temperature–composition phase diagrams such as this are often mapped out experimentally by observing the cooling curve (temperature as a function of time) along isopleths of various compositions. This procedure is thermal analysis. A break in the slope of a cooling curve at a particular temperature indicates the system point has moved from a one-phase liquid area to a two-phase area of liquid and solid. A temperature halt indicates the temperature is either the freezing point of the liquid to form a solid of the same composition, or else a eutectic temperature.
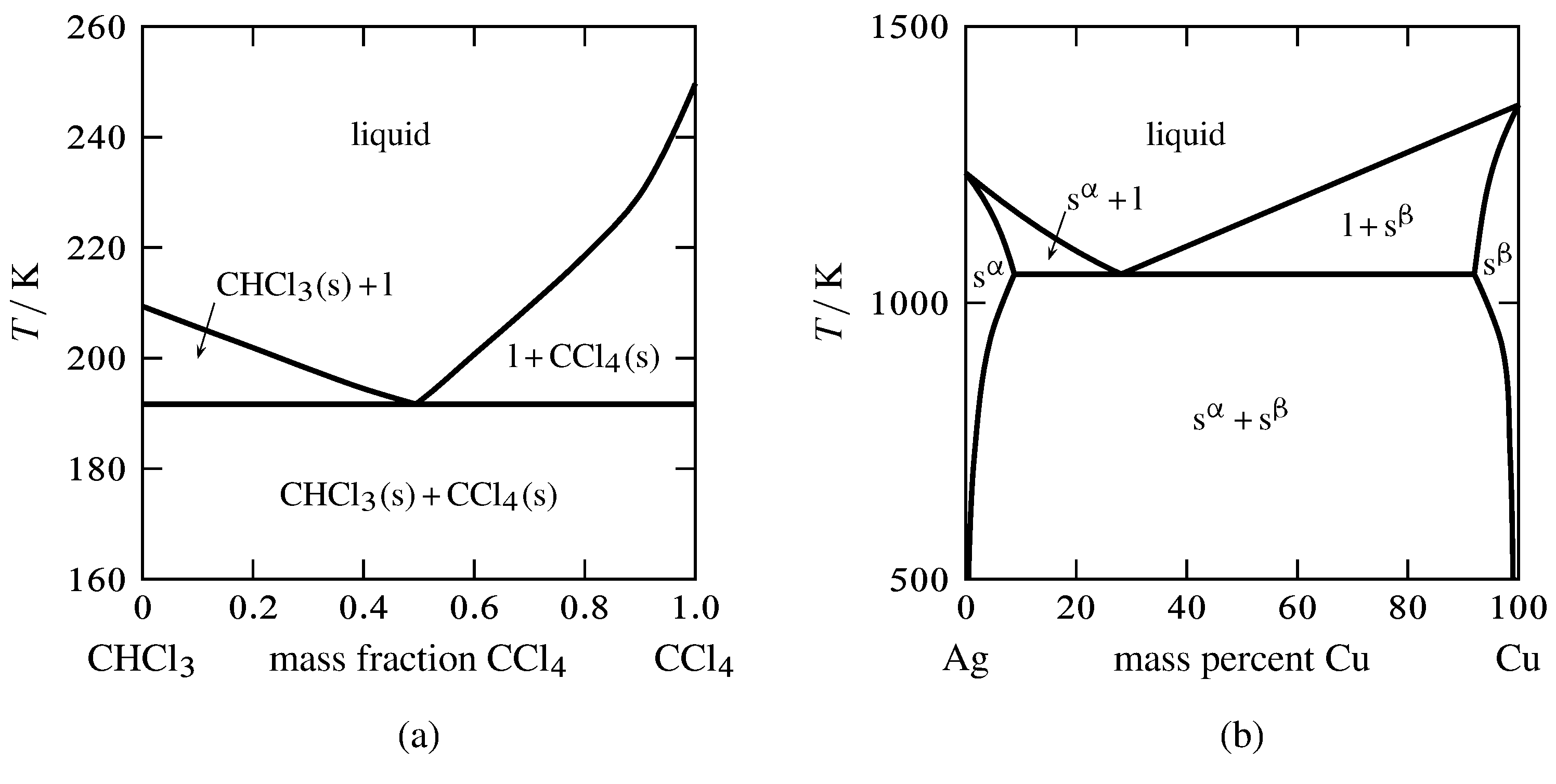
Figure 13.2 Temperature–composition phase diagrams with single eutectics.
(a) Two pure solids and a liquid mixture (E. W. Washburn, International Critical Tables of Numerical Data, Physics, Chemistry and Technology, Vol. IV, McGraw-Hill, New York, 1928, p. 98).
(b) Two solid solutions and a liquid mixture.
Figure 13.2 shows two temperature–composition phase diagrams with single eutectic points. The left-hand diagram is for the binary system of chloroform and carbon tetrachloride, two liquids that form nearly ideal mixtures. The solid phases are pure crystals, as in Fig. 13.1. The right-hand diagram is for the silver–copper system and involves solid phases that are solid solutions (substitutional alloys of variable composition). The area labeled s\(\aph\) is a solid solution that is mostly silver, and s\(\bph\) is a solid solution that is mostly copper. Tie lines in the two-phase areas do not end at a vertical line for a pure solid component as they do in the system shown in the left-hand diagram. The three phases that can coexist at the eutectic temperature of \(\tx{1,052}\K\) are the melt of the eutectic composition and the two solid solutions.
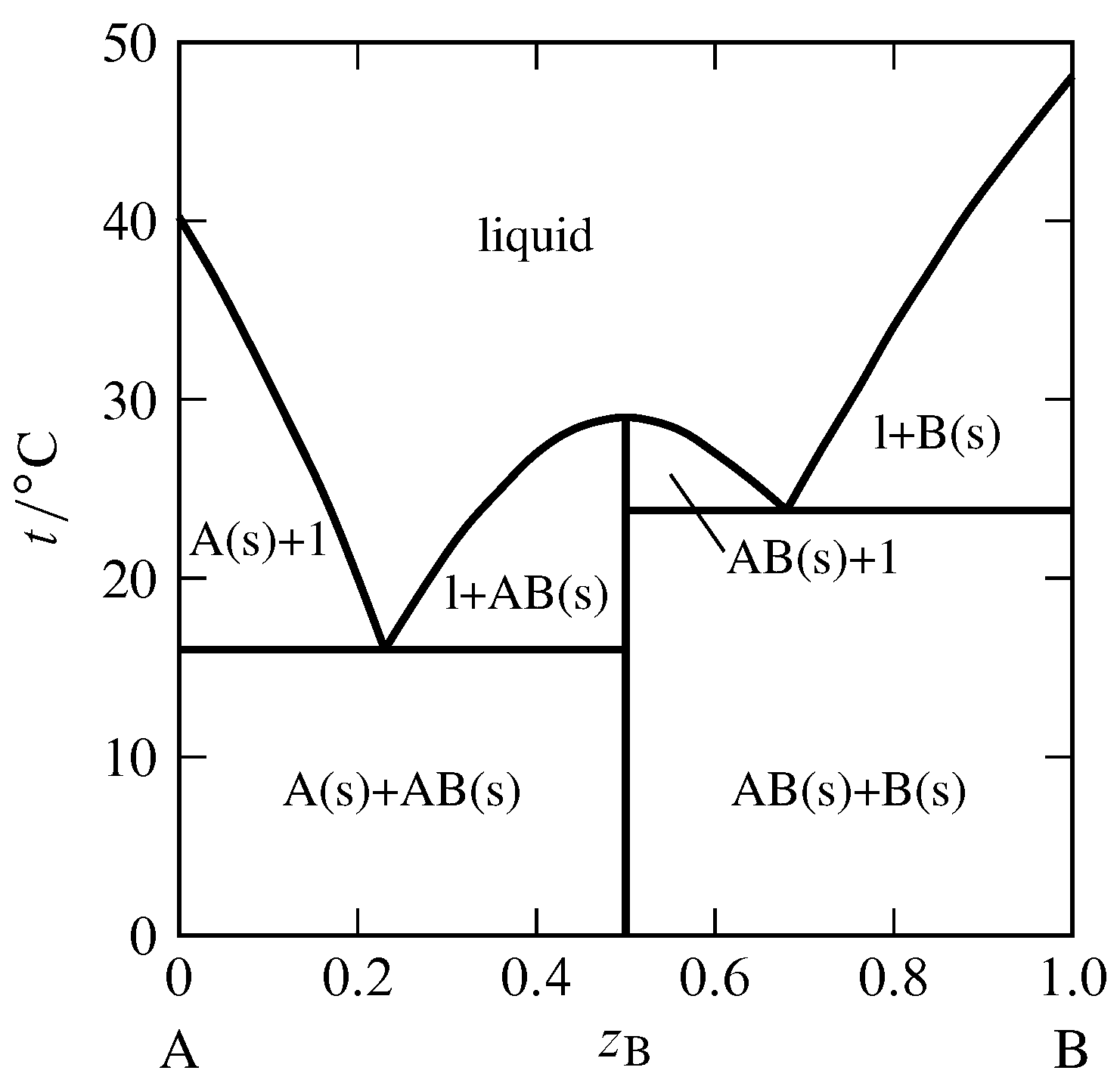
Figure 13.3 Temperature–composition phase diagram for the binary system of \(\alpha\)-naphthylamine (A) and phenol (B) at \(1\br\) (J. C. Philip, J. Chem. Soc., 83, 814–834, 1903).
Section 12.5.4 discussed the possibility of the appearance of a solid compound when a binary liquid mixture is cooled. An example of this behavior is shown in Fig. 13.3, in which the solid compound contains equal amounts of the two components \(\alpha\)-naphthylamine and phenol. The possible solid phases are pure A, pure B, and the solid compound AB. Only one or two of these solids can be present simultaneously in an equilibrium state. The vertical line in the figure at \(z\B=0.5\) represents the solid compound. The temperature at the upper end of this line is the melting point of the solid compound, \(29\units{\(\degC\)}\). The solid melts congruently to give a liquid of the same composition. A melting process with this behavior is called a dystectic reaction. The cooling curve for liquid of this composition would display a halt at the melting point.
The phase diagram in Fig. 13.3 has two eutectic points. It resembles two simple phase diagrams like Fig. 13.1 placed side by side. There is one important difference: the slope of the freezing-point curve (liquidus curve) is nonzero at the composition of a pure component, but is zero at the composition of a solid compound that is completely dissociated in the liquid (as derived theoretically in Sec. 12.5.4). Thus, the curve in Fig. 13.3 has a relative maximum at the composition of the solid compound (\(z\B=0.5\)) and is rounded there, instead of having a cusp—like a Romanesque arch rather than a Gothic arch.
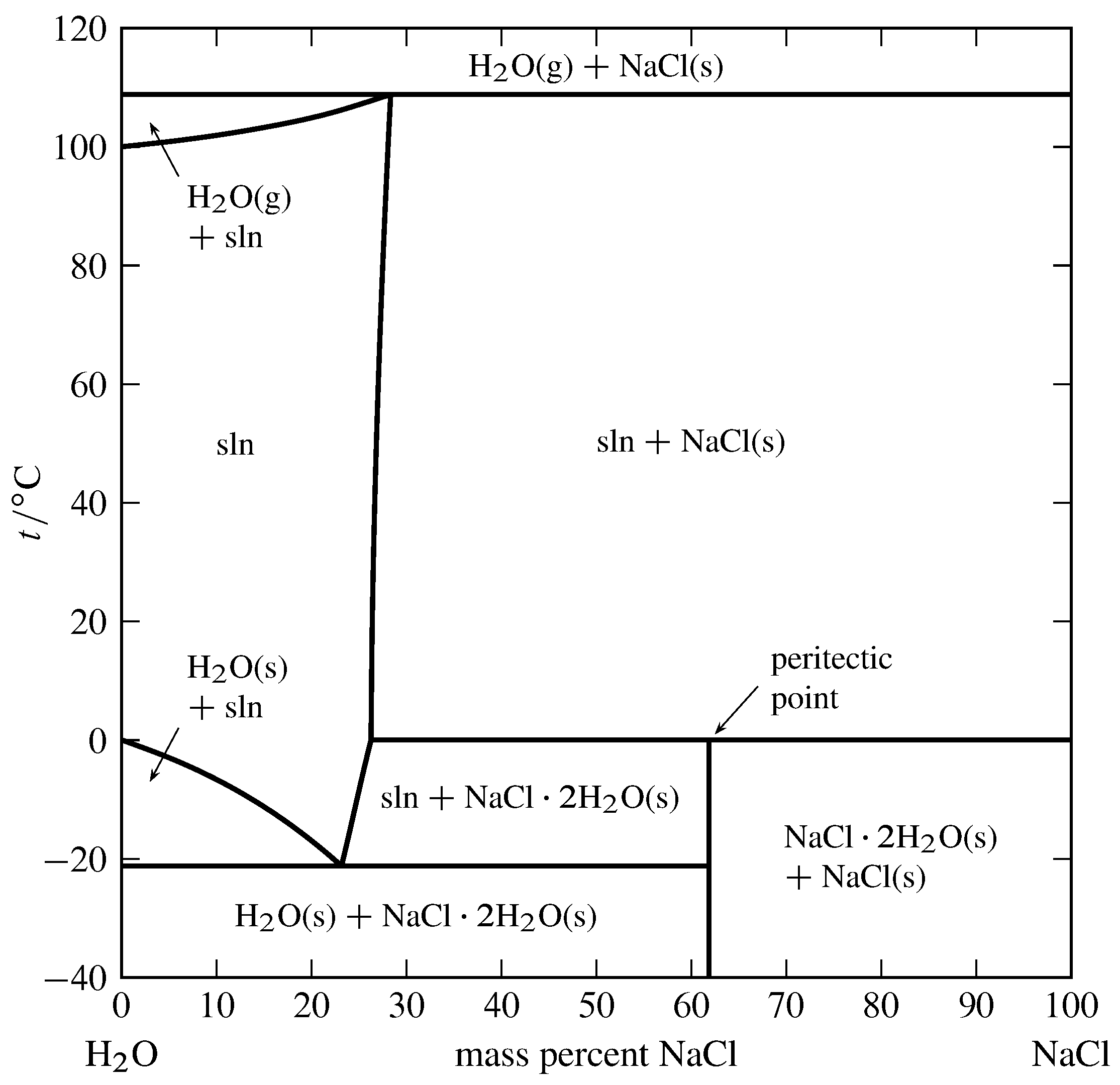
Figure 13.4 Temperature–composition phase diagram for the binary system of H\(_2\)O and NaCl at \(1\br\). (Data from Roger Cohen-Adad and John W. Lorimer, Alkali Metal and Ammonium Chlorides in Water and Heavy Water (Binary Systems), Solubility Data Series, Vol. 47, Pergamon Press, Oxford, 1991; and E. W. Washburn, International Critical Tables of Numerical Data, Physics, Chemistry and Technology, Vol. III, McGraw-Hill, New York, 1928.)
An example of a solid compound that does not melt congruently is shown in Fig. 13.4. The solid hydrate \(\ce{NaCl*2H2O}\) is \(61.9\%\) NaCl by mass. It decomposes at \(0\units{\(\degC\)}\) to form an aqueous solution of composition \(26.3\%\) NaCl by mass and a solid phase of anhydrous NaCl. These three phases can coexist at equilibrium at \(0\units{\(\degC\)}\). A phase transition like this, in which a solid compound changes into a liquid and a different solid, is called incongruent or peritectic melting, and the point on the phase diagram at this temperature at the composition of the liquid is a peritectic point.
Figure 13.4 shows there are two other temperatures at which three phases can be present simultaneously: \(-21\units{\(\degC\)}\), where the phases are ice, the solution at its eutectic point, and the solid hydrate; and \(109\units{\(\degC\)}\), where the phases are gaseous H\(_2\)O, a solution of composition \(28.3\%\) NaCl by mass, and solid NaCl. Note that both segments of the right-hand boundary of the one-phase solution area have positive slopes, meaning that the solubilities of the solid hydrate and the anhydrous salt both increase with increasing temperature.
13.2.3 Partially-miscible liquids
When two liquids that are partially miscible are combined in certain proportions, phase separation occurs (Sec. 11.1.6). Two liquid phases in equilibrium with one another are called conjugate phases. Obviously the two phases must have different compositions or they would be identical; the difference is called a miscibility gap. A binary system with two phases has two degrees of freedom, so that at a given temperature and pressure each conjugate phase has a fixed composition.
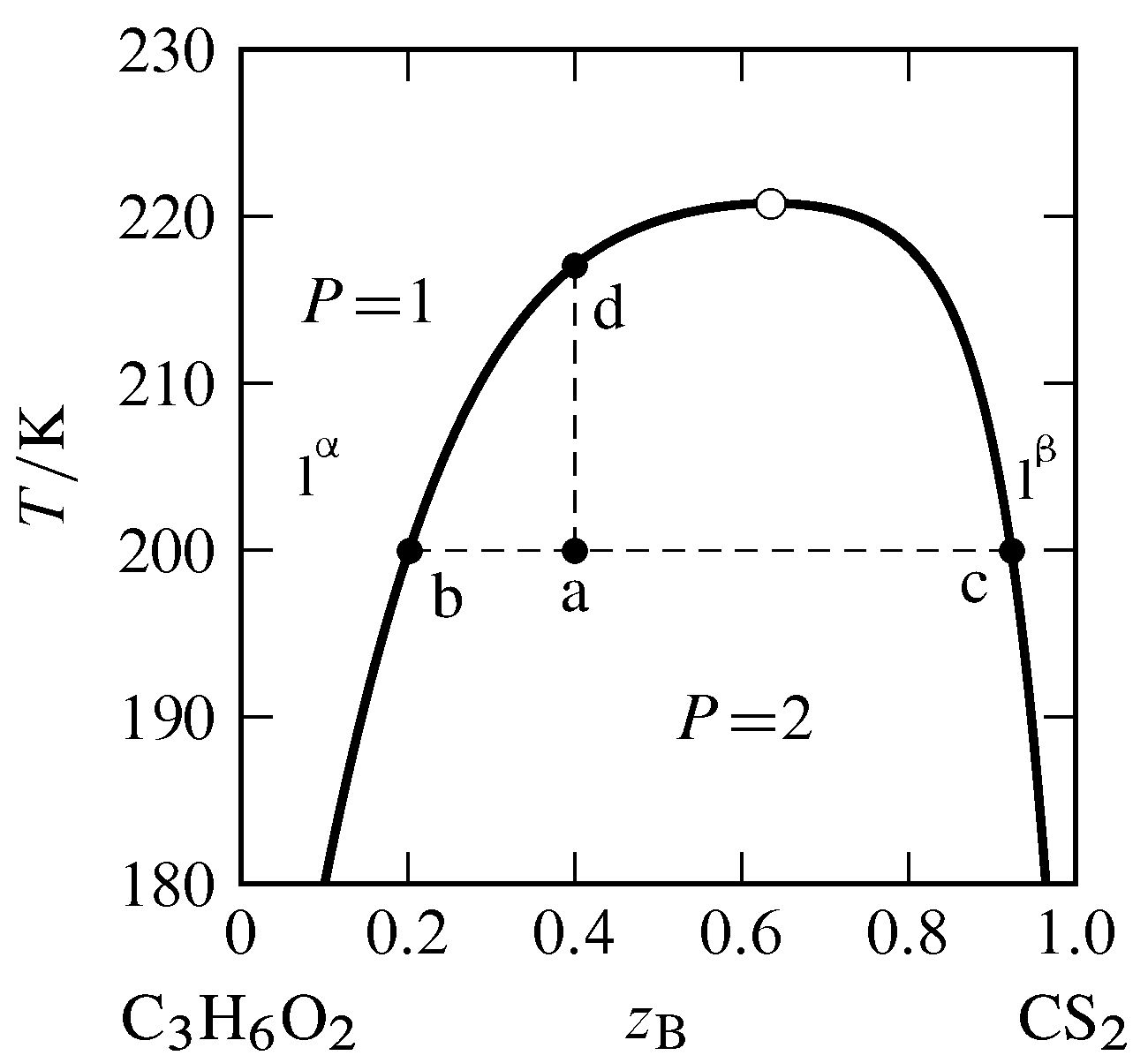
Figure 13.5 Temperature–composition phase diagram for the binary system of methyl acetate (A) and carbon disulfide (B) at \(1\br\) (data from P. Ferloni and G. Spinolo, Int. DATA Ser., Sel. Data Mixtures, Ser. A, 70, 1974). All phases are liquids. The open circle indicates the critical point.
The typical dependence of a miscibility gap on temperature is shown in Fig. 13.5. The miscibility gap (the difference in compositions at the left and right boundaries of the two-phase area) decreases as the temperature increases until at the upper consolute temperature, also called the upper critical solution temperature, the gap vanishes. The point at the maximum of the boundary curve of the two-phase area, where the temperature is the upper consolute temperature, is the consolute point or critical point. At this point, the two liquid phases become identical, just as the liquid and gas phases become identical at the critical point of a pure substance. Critical opalescence (Sec. 8.2.3) is observed in the vicinity of this point, caused by large local composition fluctuations. At temperatures at and above the critical point, the system is a single binary liquid mixture.
Suppose we combine \(6.0\mol\) of component A (methyl acetate) and \(4.0\mol\) of component B (carbon disulfide) in a cylindrical vessel and adjust the temperature to \(200\K\). The overall mole fraction of B is \(z\B=0.40\). The system point is at point a in the two-phase region. From the positions of points b and c at the ends of the tie line through point a, we find the two liquid layers have compositions \(x\B\aph=0.20\) and \(x\B\bph=0.92\). Since carbon disulfide is the more dense of the two pure liquids, the bottom layer is phase \(\phb\), the layer that is richer in carbon disulfide. According to the lever rule, the ratio of the amounts in the two phases is given by \begin{equation} \frac{n\bph}{n\aph} = \frac{z\B-x\B\aph}{x\B\bph-z\B} = \frac{0.40-0.20}{0.92-0.40} = 0.38 \tag{13.2.2} \end{equation} Combining this value with \(n\aph+n\bph=10.0\mol\) gives us \(n\aph=7.2\mol\) and \(n\bph=2.8\mol\).
If we gradually add more carbon disulfide to the vessel while gently stirring and keeping the temperature constant, the system point moves to the right along the tie line. Since the ends of this tie line have fixed positions, neither phase changes its composition, but the amount of phase \(\phb\) increases at the expense of phase \(\pha\). The liquid–liquid interface moves up in the vessel toward the top of the liquid column until, at overall composition \(z\B=0.92\) (point c), there is only one liquid phase.
Now suppose the system point is back at point a and we raise the temperature while keeping the overall composition constant at \(z\B=0.40\). The system point moves up the isopleth a–d. The phase diagram shows that the ratio \((z\B-x\B\aph)/(x\B\bph-z\B)\) decreases during this change. As a result, the amount of phase \(\pha\) increases, the amount of phase \(\phb\) decreases, and the liquid–liquid interface moves down toward the bottom of the vessel until at \(217\K\) (point d) there again is only one liquid phase.
13.2.4 Liquid–gas systems with ideal liquid mixtures
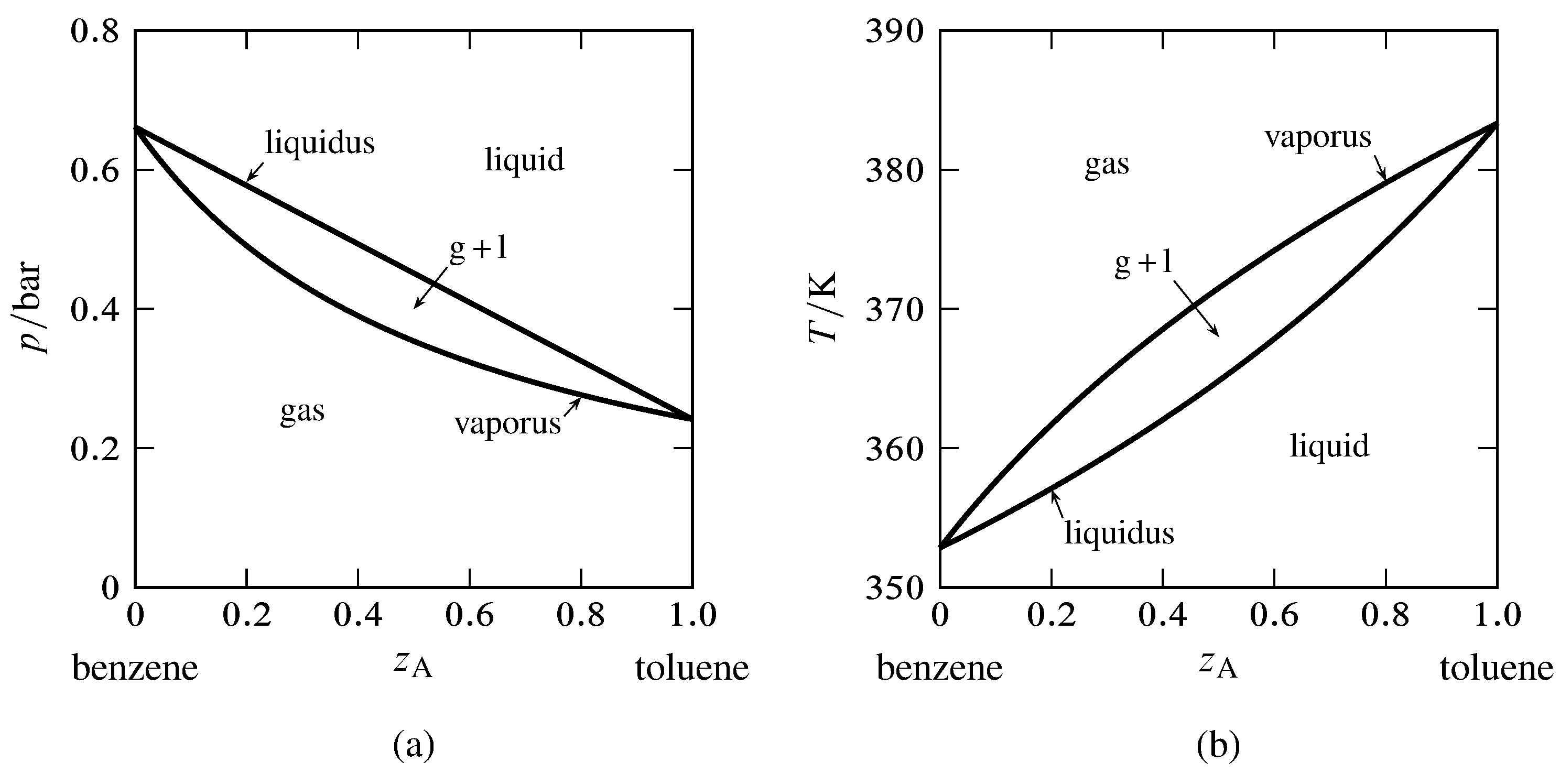
Figure 13.6 Phase diagrams for the binary system of toluene (A) and benzene (B). The curves are calculated from Eqs. 13.2.6 and 13.2.7 and the saturation vapor pressures of the pure liquids.
(a) Pressure–composition diagram at \(T=340\K\).
(b) Temperature–composition diagram at \(p=1\br\).
Toluene and benzene form liquid mixtures that are practically ideal and closely obey Raoult’s law for partial pressure. For the binary system of these components, we can use the vapor pressures of the pure liquids to generate the liquidus and vaporus curves of the pressure–composition and temperature–composition phase diagram. The results are shown in Fig. 13.6. The composition variable \(z\A\) is the overall mole fraction of component A (toluene).
The equations needed to generate the curves can be derived as follows. Consider a binary liquid mixture of components A and B and mole fraction composition \(x\A\) that obeys Raoult’s law for partial pressure (Eq. 9.4.2): \begin{equation} p\A = x\A p\A^* \qquad p\B = (1-x\A)p\B^* \tag{13.2.3} \end{equation} Strictly speaking, Raoult’s law applies to a liquid–gas system maintained at a constant pressure by means of a third gaseous component, and \(p\A^*\) and \(p\B^*\) are the vapor pressures of the pure liquid components at this pressure and the temperature of the system. However, when a liquid phase is equilibrated with a gas phase, the partial pressure of a constituent of the liquid is practically independent of the total pressure (Sec. 12.8.1), so that it is a good approximation to apply the equations to a binary liquid–gas system and treat \(p\A^*\) and \(p\B^*\) as functions only of \(T\).
When the binary system contains a liquid phase and a gas phase in equilibrium, the pressure is the sum of \(p\A\) and \(p\B\), which from Eq. 13.2.3 is given by \begin{gather} \s {\begin{split} p & = x\A p\A^* + (1-x\A)p\B^* \cr & = p\B^* + (p\A^*-p\B^*)x\A \end{split} } \tag{13.2.4} \cond{(\(C{=}2\), ideal liquid mixture)} \end{gather} where \(x\A\) is the mole fraction of A in the liquid phase. Equation 13.2.4 shows that in the two-phase system, \(p\) has a value between \(p\A^*\) and \(p\B^*\), and that if \(T\) is constant, \(p\) is a linear function of \(x\A\). The mole fraction composition of the gas in the two-phase system is given by \begin{equation} y\A = \frac{p\A}{p} = \frac{x\A p\A^*}{p\B^* + (p\A^*-p\B^*)x\A } \tag{13.2.5} \end{equation}
A binary two-phase system has two degrees of freedom. At a given \(T\) and \(p\), each phase must have a fixed composition. We can calculate the liquid composition by rearranging Eq. 13.2.4: \begin{gather} \s {x\A = \frac{p-p\B^*}{p\A^*-p\B^*}} \tag{13.2.6} \cond{(\(C{=}2\), ideal liquid mixture)} \end{gather} The gas composition is then given by \begin{gather} \s {\begin{split} y\A & = \frac{p\A}{p} = \frac{x\A p\A^*}{p} \cr & = \left( \frac{p-p\B^*}{p\A^*-p\B^*}\right) \frac{p\A^*}{p} \end{split} } \tag{13.2.7} \cond{(\(C{=}2\), ideal liquid mixture)} \end{gather}
If we know \(p\A^*\) and \(p\B^*\) as functions of \(T\), we can use Eqs. 13.2.6 and 13.2.7 to calculate the compositions for any combination of \(T\) and \(p\) at which the liquid and gas phases can coexist, and thus construct a pressure–composition or temperature–composition phase diagram.
In Fig. 13.6(a), the liquidus curve shows the relation between \(p\) and \(x\A\) for equilibrated liquid and gas phases at constant \(T\), and the vaporus curve shows the relation between \(p\) and \(y\A\) under these conditions. We see that \(p\) is a linear function of \(x\A\) but not of \(y\A\).
In a similar fashion, the liquidus curve in Fig. 13.6(b) shows the relation between \(T\) and \(x\A\), and the vaporus curve shows the relation between \(T\) and \(y\A\), for equilibrated liquid and gas phases at constant \(p\). Neither curve is linear.
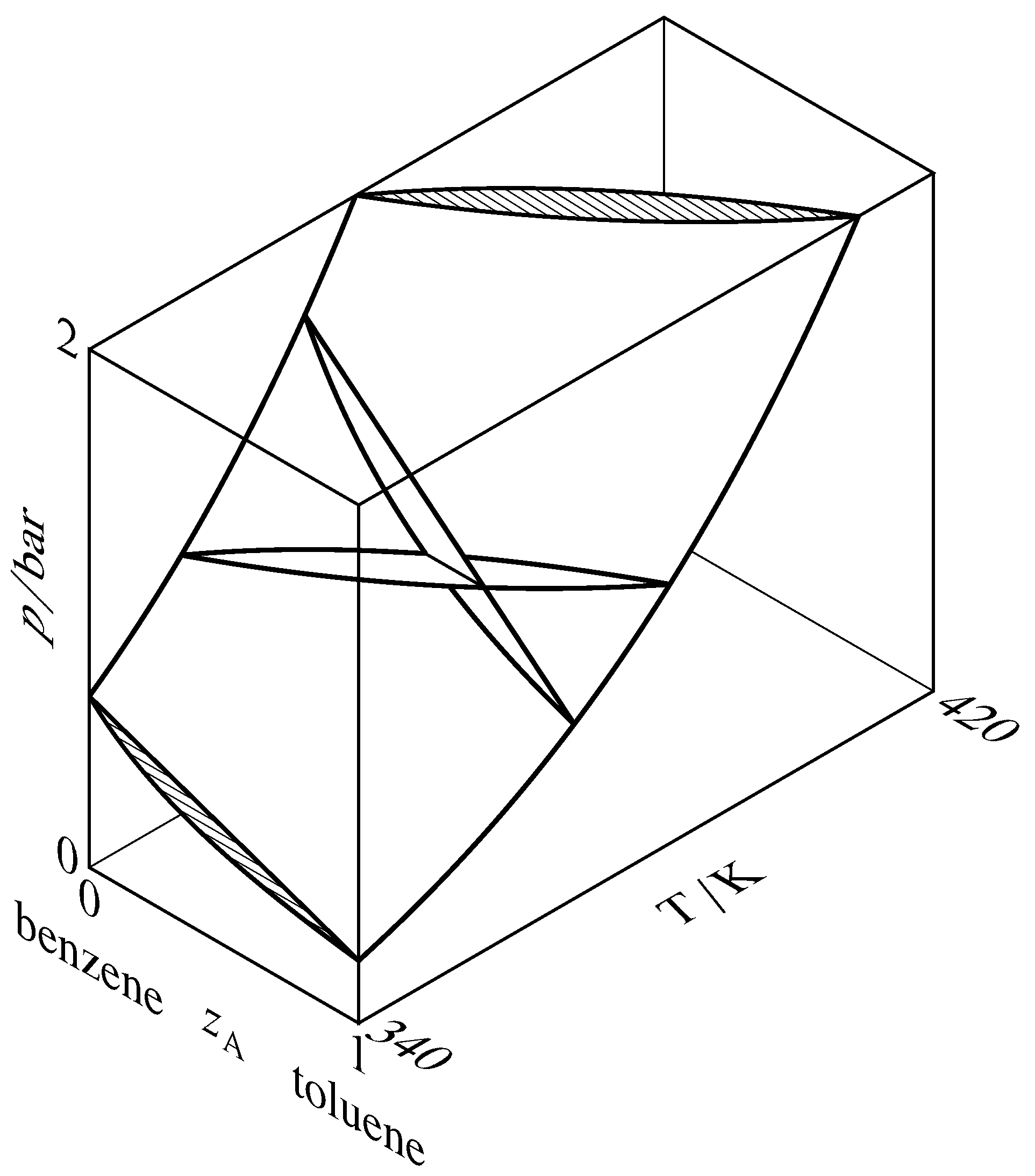
Figure 13.7 Liquidus and vaporus surfaces for the binary system of toluene (A) and benzene. Cross-sections through the two-phase region are drawn at constant temperatures of \(340\K\) and \(370\K\) and at constant pressures of \(1\br\) and \(2\br\). Two of the cross-sections intersect at a tie line at \(T=370\K\) and \(p=1\br\), and the other cross-sections are hatched in the direction of the tie lines.
A liquidus curve is also called a bubble-point curve or a boiling-point curve. Other names for a vaporus curve are dew-point curve and condensation curve. These curves are actually cross-sections of liquidus and vaporus surfaces in a three-dimensional \(T\)–\(p\)–\(z\A\) phase diagram, as shown in Fig. 13.7. In this figure, the liquidus surface is in view at the front and the vaporus surface is hidden behind it.
13.2.5 Liquid–gas systems with nonideal liquid mixtures
Most binary liquid mixtures do not behave ideally. The most common situation is positive deviations from Raoult’s law. (In the molecular model of Sec. 11.1.5, positive deviations correspond to a less negative value of \(k\subs{AB}\) than the average of \(k\subs{AA}\) and \(k\subs{BB}\).) Some mixtures, however, have specific A–B interactions, such as solvation or molecular association, that prevent random mixing of the molecules of A and B, and the result is then negative deviations from Raoult’s law. If the deviations from Raoult’s law, either positive or negative, are large enough, the constant-temperature liquidus curve exhibits a maximum or minimum and azeotropic behavior results.
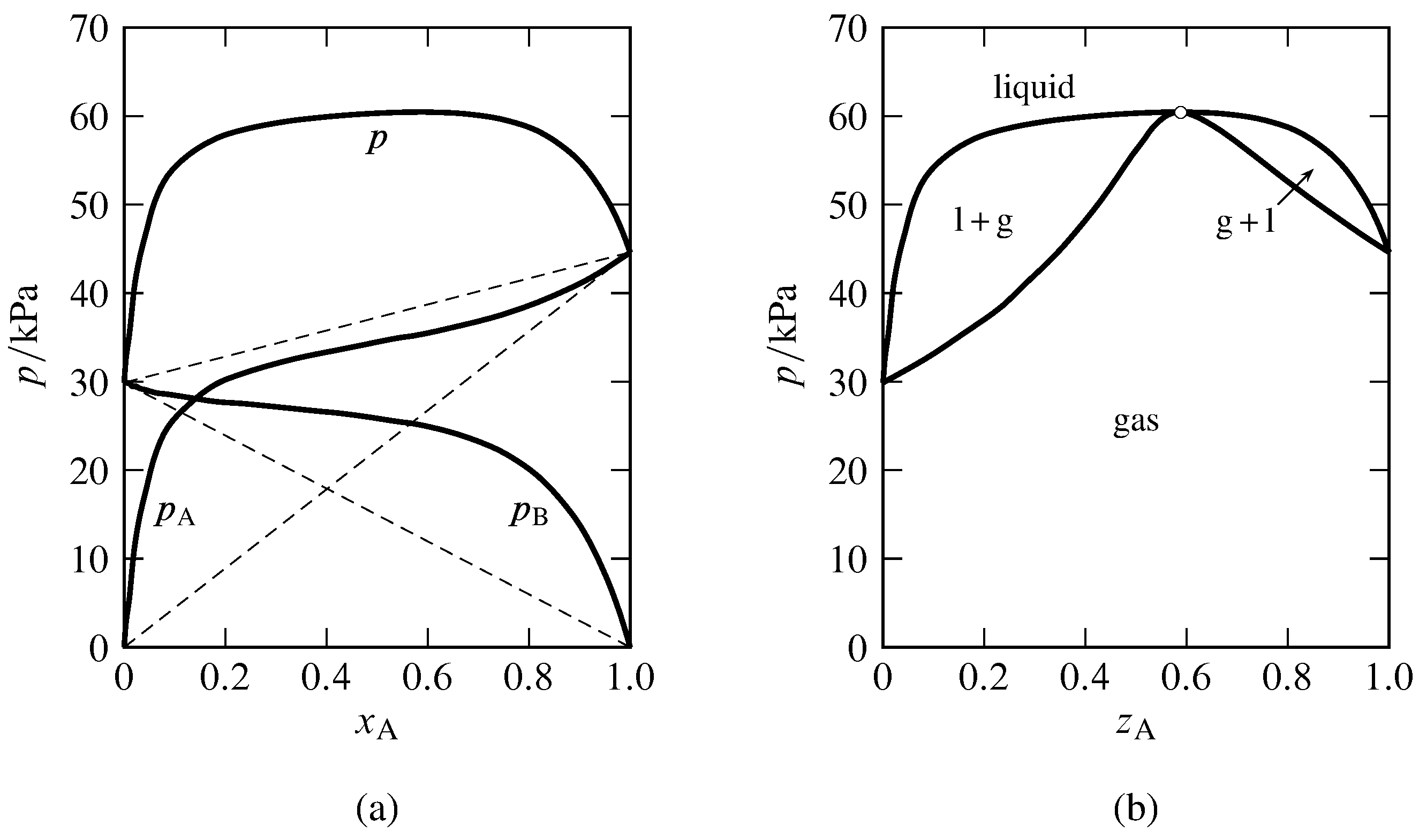
Figure 13.8 Binary system of methanol (A) and benzene at \(45\units{\(\degC\)}\) (Hossein Toghiani, Rebecca K. Toghiani, and Dabir S. Viswanath, J. Chem. Eng. Data, 39, 63–67, 1994).
(a) Partial pressures and total pressure in the gas phase equilibrated with liquid mixtures. The dashed lines indicate Raoult’s law behavior.
(b) Pressure–composition phase diagram at \(45\units{\(\degC\)}\). Open circle: azeotropic point at \(z\A=0.59\) and \(p=60.5\units{kPa}\).
Figure 13.8 shows the azeotropic behavior of the binary methanol-benzene system at constant temperature. In Fig. 13.8(a), the experimental partial pressures in a gas phase equilibrated with the nonideal liquid mixture are plotted as a function of the liquid composition. The partial pressures of both components exhibit positive deviations from Raoult’s law, consistent with the statement in Sec. 12.8.2 that if one constituent of a binary liquid mixture exhibits positive deviations from Raoult’s law, with only one inflection point in the curve of fugacity versus mole fraction, the other constituent also has positive deviations from Raoult’s law. The total pressure (equal to the sum of the partial pressures) has a maximum value greater than the vapor pressure of either pure component. The curve of \(p\) versus \(x\A\) becomes the liquidus curve of the pressure–composition phase diagram shown in Fig. 13.8(b). Points on the vaporus curve are calculated from \(p=p\A/y\A\).
In practice, the data needed to generate the liquidus and vaporus curves of a nonideal binary system are usually obtained by allowing liquid mixtures of various compositions to boil in an equilibrium still at a fixed temperature or pressure. When the liquid and gas phases have become equilibrated, samples of each are withdrawn for analysis. The partial pressures shown in Fig. 13.8(a) were calculated from the experimental gas-phase compositions with the relations \(p\A=y\A p\) and \(p\B=p-p\A\).
If the constant-temperature liquidus curve has a maximum pressure at a liquid composition not corresponding to one of the pure components, which is the case for the methanol–benzene system, then the liquid and gas phases are mixtures of identical compositions at this pressure. This behavior was deduced at the end of Sec. 12.8.3. On the pressure–composition phase diagram, the liquidus and vaporus curves both have maxima at this pressure, and the two curves coincide at an azeotropic point. A binary system with negative deviations from Raoult’s law can have an isothermal liquidus curve with a minimum pressure at a particular mixture composition, in which case the liquidus and vaporus curves coincide at an azeotropic point at this minimum. The general phenomenon in which equilibrated liquid and gas mixtures have identical compositions is called azeotropy, and the liquid with this composition is an azeotropic mixture or azeotrope (Greek: boils unchanged). An azeotropic mixture vaporizes as if it were a pure substance, undergoing an equilibrium phase transition to a gas of the same composition.
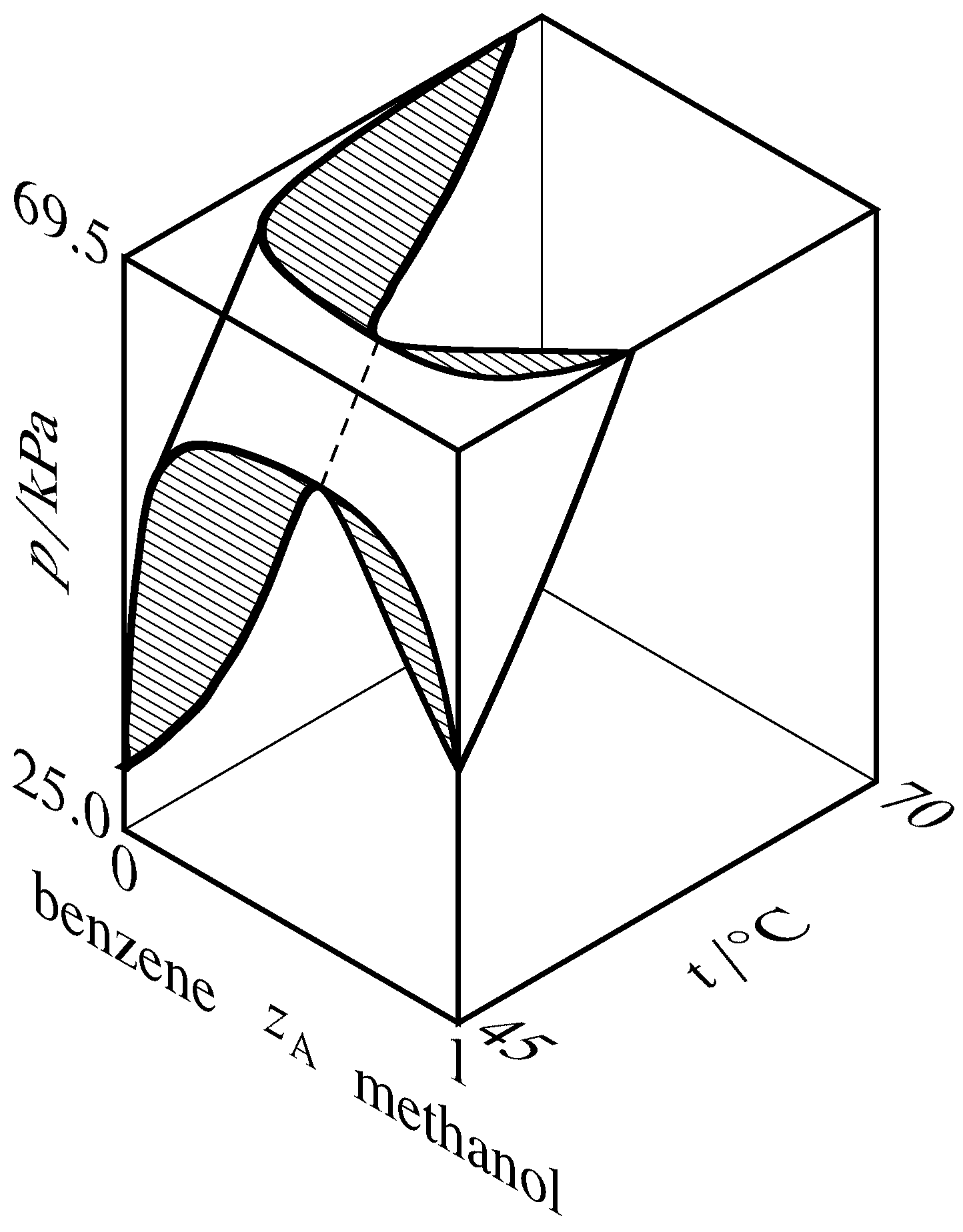
Figure 13.9 Liquidus and vaporus surfaces for the binary system of methanol (A) and benzene (Hossein Toghiani, Rebecca K. Toghiani, and Dabir S. Viswanath, J. Chem. Eng. Data, 39, 63–67, 1994). Cross-sections are hatched in the direction of the tie lines. The dashed curve is the azeotrope vapor-pressure curve.
If the liquidus and vaporus curves exhibit a maximum on a pressure–composition phase diagram, then they exhibit a minimum on a temperature–composition phase diagram. This relation is explained for the methanol–benzene system by the three-dimensional liquidus and vaporus surfaces drawn in Fig. 13.9. In this diagram, the vaporus surface is hidden behind the liquidus surface. The hatched cross-section at the front of the figure is the same as the pressure–composition diagram of Fig. 13.8(b), and the hatched cross-section at the top of the figure is a temperature–composition phase diagram in which the system exhibits a minimum-boiling azeotrope.
A binary system containing an azeotropic mixture in equilibrium with its vapor has two species, two phases, and one relation among intensive variables: \(x\A =y\A\). The number of degrees of freedom is then \(F = 2+s-r-P = 2+2-1-2 = 1\); the system is univariant. At a given temperature, the azeotrope can exist at only one pressure and have only one composition. As \(T\) changes, so do \(p\) and \(z\A\) along an azeotrope vapor-pressure curve as illustrated by the dashed curve in Fig. 13.9.
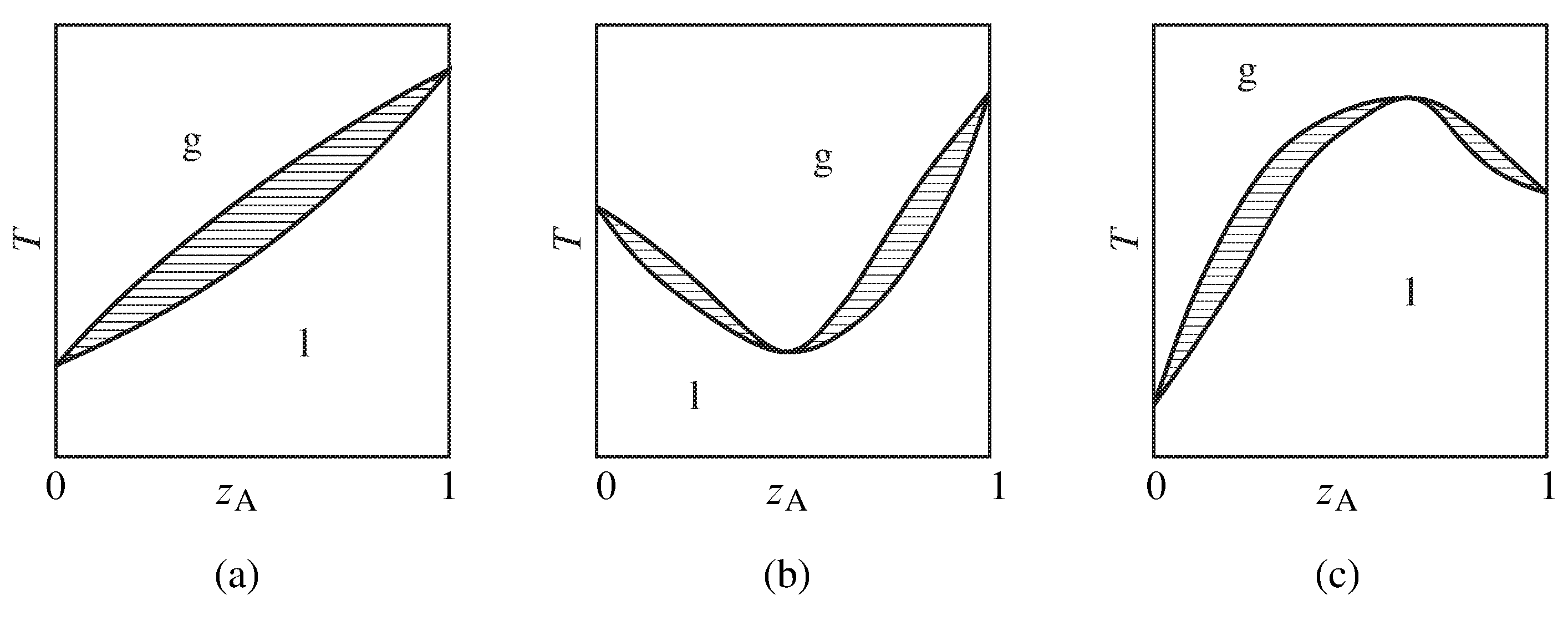
Figure 13.10 Temperature–composition phase diagrams of binary systems exhibiting (a) no azeotropy, (b) a minimum-boiling azeotrope, and (c) a maximum-boiling azeotrope. Only the one-phase areas are labeled; two-phase areas are hatched in the direction of the tie lines.
Figure 13.10 summarizes the general appearance of some relatively simple temperature–composition phase diagrams of binary systems. If the system does not form an azeotrope (zeotropic behavior), the equilibrated gas phase is richer in one component than the liquid phase at all liquid compositions, and the liquid mixture can be separated into its two components by fractional distillation. The gas in equilibrium with an azeotropic mixture, however, is not enriched in either component. Fractional distillation of a system with an azeotrope leads to separation into one pure component and the azeotropic mixture.
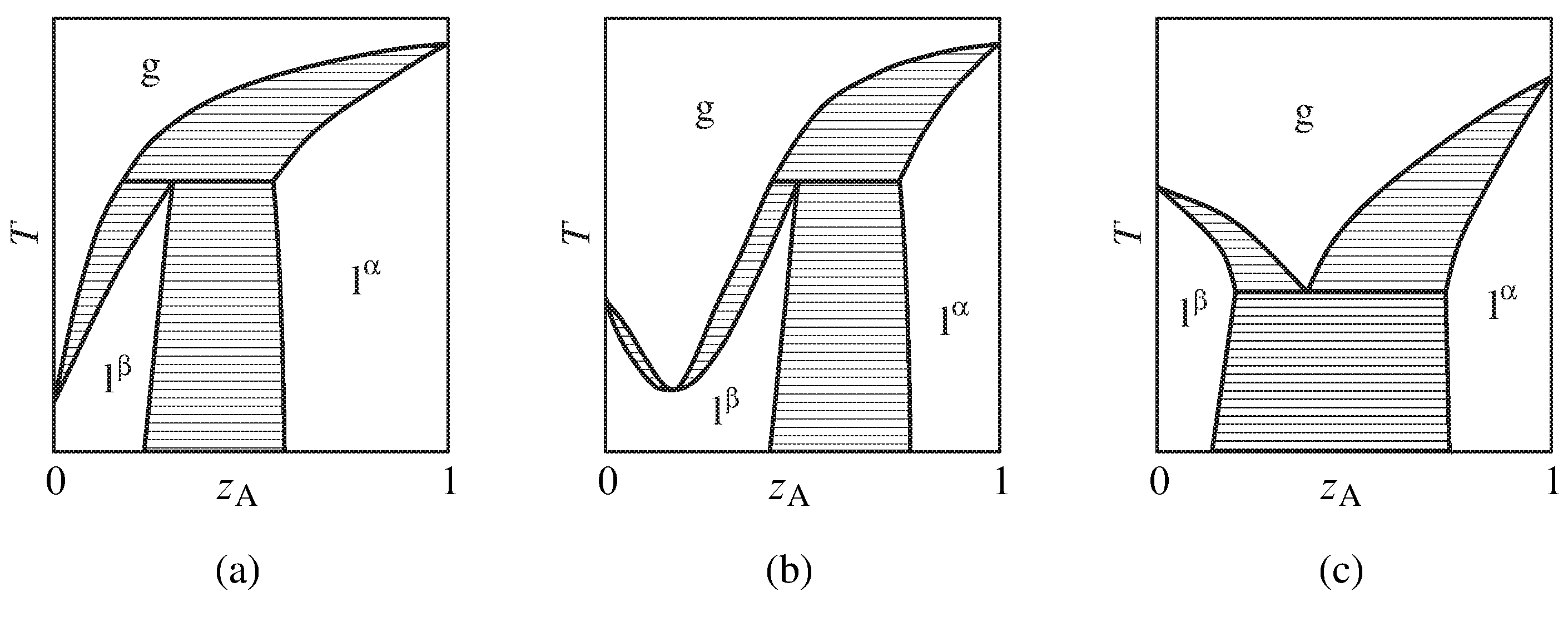
Figure 13.11 Temperature–composition phase diagrams of binary systems with partially-miscible liquids exhibiting (a) the ability to be separated into pure components by fractional distillation, (b) a minimum-boiling azeotrope, and (c) boiling at a lower temperature than the boiling point of either pure component. Only the one-phase areas are labeled; two-phase areas are hatched in the direction of the tie lines.
More complicated behavior is shown in the phase diagrams of Fig. 13.11. These are binary systems with partially-miscible liquids in which the boiling point is reached before an upper consolute temperature can be observed.
13.2.6 Solid–gas systems
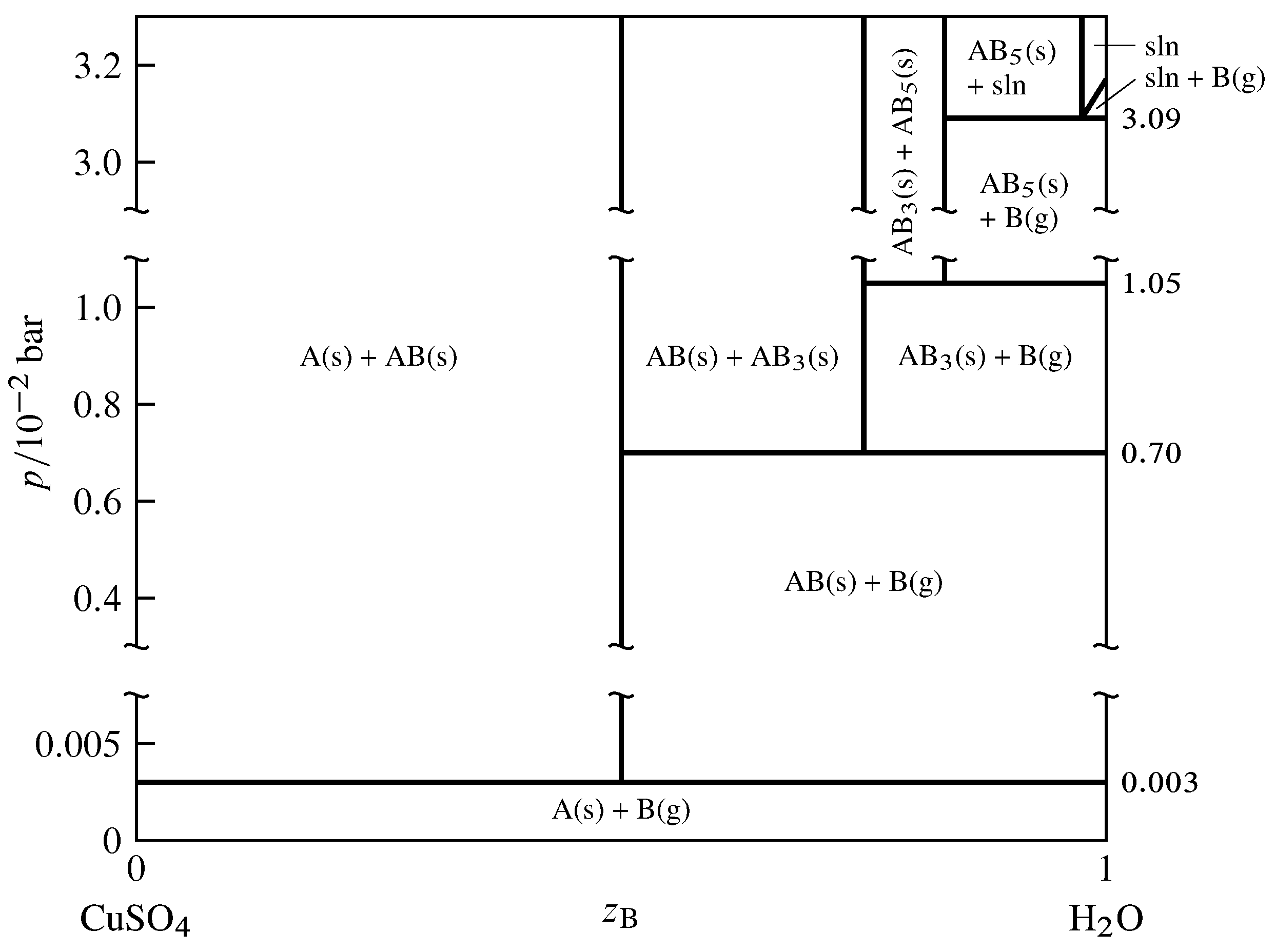
Figure 13.12 Pressure–composition phase diagram for the binary system of CuSO\(_4\) (A) and H\(_2\)O (B) at \(25\units{\(\degC\)}\) (Thomas S. Logan, J. Chem. Educ., 35, 148–149, 1958; E. W. Washburn, International Critical Tables of Numerical Data, Physics, Chemistry and Technology, Vol. VII, McGraw-Hill, New York, 1930, p. 263).
As an example of a two-component system with equilibrated solid and gas phases, consider the components \(\ce{CuSO4}\) and \(\ce{H2O}\), denoted A and B respectively. In the pressure–composition phase diagram shown in Fig. 13.12, the composition variable \(z\B\) is as usual the mole fraction of component B in the system as a whole.
The anhydrous salt and its hydrates (solid compounds) form the series of solids \(\ce{CuSO4}\), \(\ce{CuSO4*H2O}\), \(\ce{CuSO4*3H2O}\), and \(\ce{CuSO4*5H2O}\). In the phase diagram these formulas are abbreviated A, AB, AB\(_3\), and AB\(_5\). The following dissociation equilibria (dehydration equilibria) are possible: \begin{align*} \ce{CuSO4*H2O}\tx{(s)} & \arrows \ce{CuSO4}\tx{(s)} + \ce{H2O}\tx{(g)}\cr \ce{1/2CuSO4*3H2O}\tx{(s)} & \arrows \ce{1/2CuSO4*H2O}\tx{(s)} + \ce{H2O}\tx{(g)}\cr \ce{1/2CuSO4*5H2O}\tx{(s)} & \arrows \ce{1/2CuSO4*3H2O}\tx{(s)} + \ce{H2O}\tx{(g)} \end{align*} The equilibria are written above with coefficients that make the coefficient of H\(_2\)O(g) unity. When one of these equilibria is established in the system, there are two components and three phases; the phase rule then tells us the system is univariant and the pressure has only one possible value at a given temperature. This pressure is called the dissociation pressure of the higher hydrate.
The dissociation pressures of the three hydrates are indicated by horizontal lines in Fig. 13.12. For instance, the dissociation pressure of \(\ce{CuSO4*5H2O}\) is \(1.05\timesten{-2}\units{\(\br\)}\). At the pressure of each horizontal line, the equilibrium system can have one, two, or three phases, with compositions given by the intersections of the line with vertical lines. A fourth three-phase equilibrium is shown at \(p=3.09\timesten{-2}\units{\(\br\)}\); this is the equilibrium between solid \(\ce{CuSO4*5H2O}\), the saturated aqueous solution of this hydrate, and water vapor.
Consider the thermodynamic equilibrium constant of one of the dissociation reactions. At the low pressures shown in the phase diagram, the activities of the solids are practically unity and the fugacity of the water vapor is practically the same as the pressure, so the equilibrium constant is almost exactly equal to \(p\subs{d}/p\st\), where \(p\subs{d}\) is the dissociation pressure of the higher hydrate in the reaction. Thus, a hydrate cannot exist in equilibrium with water vapor at a pressure below the dissociation pressure of the hydrate because dissociation would be spontaneous under these conditions. Conversely, the salt formed by the dissociation of a hydrate cannot exist in equilibrium with water vapor at a pressure above the dissociation pressure because hydration would be spontaneous.
If the system contains dry air as an additional gaseous component and one of the dissociation equilibria is established, the partial pressure \(p\subs{H\(_2\)O}\) of H\(_2\)O is equal (approximately) to the dissociation pressure \(p\subs{d}\) of the higher hydrate. The prior statements regarding dissociation and hydration now depend on the value of \(p\subs{H\(_2\)O}\). If a hydrate is placed in air in which \(p\subs{H\(_2\)O}\) is less than \(p\subs{d}\), dehydration is spontaneous; this phenomenon is called efflorescence (Latin: blossoming). If \(p\subs{H\(_2\)O}\) is greater than the vapor pressure of the saturated solution of the highest hydrate that can form in the system, the anhydrous salt and any of its hydrates will spontaneously absorb water and form the saturated solution; this is deliquescence (Latin: becoming fluid).
If the two-component equilibrium system contains only two phases, it is bivariant corresponding to one of the areas in Fig. 13.12. Here both the temperature and the pressure can be varied. In the case of areas labeled with two solid phases, the pressure has to be applied to the solids by a fluid (other than H\(_2\)O) that is not considered part of the system.
13.2.7 Systems at high pressure
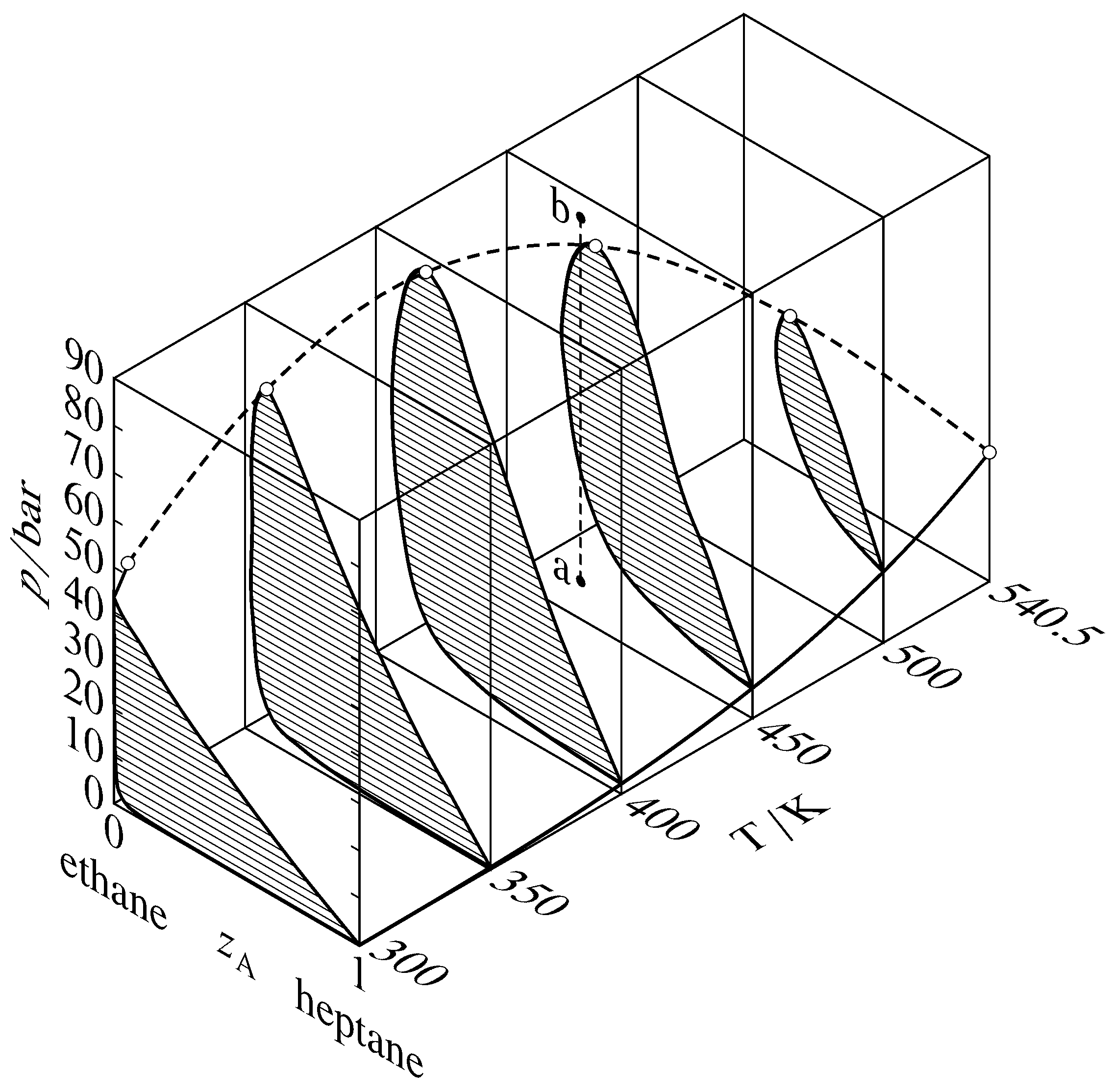
Figure 13.13 Pressure–temperature–composition behavior in the binary heptane–ethane system (W. B. Kay, Ind. Eng. Chem., 30, 459–465, 1938). The open circles are critical points; the dashed curve is the critical curve. The dashed line a–b illustrates retrograde condensation at \(450\K\).
Binary phase diagrams begin to look different when the pressure is greater than the critical pressure of either of the pure components. Various types of behavior have been observed in this region. One common type, that found in the binary system of heptane and ethane, is shown in Fig. 13.13. This figure shows sections of a three-dimensional phase diagram at five temperatures. Each section is a pressure–composition phase diagram at constant \(T\). The two-phase areas are hatched in the direction of the tie lines. At the left end of each tie line (at low \(z\A\)) is a vaporus curve, and at the right end is a liquidus curve. The vapor pressure curve of pure ethane (\(z\A{=}0\)) ends at the critical point of ethane at \(305.4\K\); between this point and the critical point of heptane at \(540.5\K\), there is a continuous critical curve, which is the locus of critical points at which gas and liquid mixtures become identical in composition and density.
Consider what happens when the system point is at point a in Fig. 13.13 and the pressure is then increased by isothermal compression along line a–b. The system point moves from the area for a gas phase into the two-phase gas–liquid area and then out into the gas-phase area again. This curious phenomenon, condensation followed by vaporization, is called retrograde condensation.
Under some conditions, an isobaric increase of \(T\) can result in vaporization followed by condensation; this is retrograde vaporization.

Figure 13.14 Pressure–temperature–composition behavior in the binary xenon–helium system (J. de Swann Arons and G. A. M. Diepen, J. Chem. Phys., 44, 2322–2330, 1966). The open circles are critical points; the dashed curve is the critical curve.
A different type of high-pressure behavior, that found in the xenon–helium system, is shown in Fig. 13.14. Here, the critical curve begins at the critical point of the less volatile component (xenon) and continues to higher temperatures and pressures than the critical temperature and pressure of either pure component. The two-phase region at pressures above this critical curve is sometimes said to represent gas–gas equilibrium, or gas–gas immiscibility, because we would not usually consider a liquid to exist beyond the critical points of the pure components. Of course, the coexisting phases in this two-phase region are not gases in the ordinary sense of being tenuous fluids, but are instead high-pressure fluids of liquid-like densities. If we want to call both phases gases, then we have to say that pure gaseous substances at high pressure do not necessarily mix spontaneously in all proportions as they do at ordinary pressures.
If the pressure of a system is increased isothermally, eventually solid phases will appear; these are not shown in Figs. 13.13 and Fig. 13.14.


