9.9: Chapter 9 Problems
- Page ID
- 23733
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)An underlined problem number or problem-part letter indicates that the numerical answer appears in Appendix I.
9.1 For a binary solution, find expressions for the mole fractions \(x_{\mathrm{B}}\) and \(x_{\mathrm{A}}\) as functions of the solute molality \(m_{\mathrm{B}}\).
9.2 Consider a binary mixture of two liquids, \(\mathrm{A}\) and \(\mathrm{B}\). The molar volume of mixing, \(\Delta V(\mathrm{mix}) / n\), is given by Eq. 9.2.19.
(a) Find a formula for calculating the value of \(\Delta V(\mathrm{mix}) / n\) of a binary mixture from values of \(x_{\mathrm{A}}, x_{\mathrm{B}}, M_{\mathrm{A}}, M_{\mathrm{B}}, \rho, \rho_{\mathrm{A}}^{*}\), and \(\rho_{\mathrm{B}}^{*} .\)
Table \(9.7\) Molar volumes of mixing of binary mixtures of 1-hexanol (A) and 1 -octene \((\mathrm{B})\) at \(25^{\circ} \mathrm{C} .^{a}\)
\begin{tabular}{lccc}
\hline\(x_{\mathrm{B}}\) & {\([\Delta V(\mathrm{mix}) / n] / \mathrm{cm}^{3} \mathrm{~mol}^{-1}\)} & \(x_{\mathrm{B}}\) & {\([\Delta V(\mathrm{mix}) / n] / \mathrm{cm}^{3} \mathrm{~mol}^{-1}\)} \\
\hline 0 & 0 & \(0.555\) & \(0.005\) \\
\(0.049\) & \(-0.027\) & \(0.597\) & \(0.011\) \\
\(0.097\) & \(-0.050\) & \(0.702\) & \(0.029\) \\
\(0.146\) & \(-0.063\) & \(0.716\) & \(0.035\) \\
\(0.199\) & \(-0.077\) & \(0.751\) & \(0.048\) \\
\(0.235\) & \(-0.073\) & \(0.803\) & \(0.056\) \\
\(0.284\) & \(-0.074\) & \(0.846\) & \(0.058\) \\
\(0.343\) & \(-0.065\) & \(0.897\) & \(0.057\) \\
\(0.388\) & \(-0.053\) & \(0.944\) & \(0.049\) \\
\(0.448\) & \(-0.032\) & 1 & 0 \\
\(0.491\) & \(-0.016\) & & \\
\hline
\end{tabular}
\({ }^{a}\) Ref. [170].
(b) The molar volumes of mixing for liquid binary mixtures of 1-hexanol (A) and 1-octene (B) at \(25^{\circ} \mathrm{C}\) have been calculated from their measured densities. The data are in Table 9.7. The molar volumes of the pure constituents are \(V_{\mathrm{A}}^{*}=125.31 \mathrm{~cm}^{3} \mathrm{~mol}^{-1}\) and \(V_{\mathrm{B}}^{*}=\) \(157.85 \mathrm{~cm}^{3} \mathrm{~mol}^{-1}\). Use the method of intercepts to estimate the partial molar volumes of both constituents in an equimolar mixture \(\left(x_{\mathrm{A}}=x_{\mathrm{B}}=0.5\right)\), and the partial molar volume \(V_{\mathrm{B}}^{\infty}\) of B at infinite dilution.
9.3 Extend the derivation of Prob. 8.1, concerning a liquid droplet of radius \(r\) suspended in a gas, to the case in which the liquid and gas are both mixtures. Show that the equilibrium conditions are \(T^{\mathrm{g}}=T^{\mathrm{l}}, \mu_{i}^{\mathrm{g}}=\mu_{i}^{1}\) (for each species \(i\) that can equilibrate between the two phases), and \(p^{1}=p^{g}+2 \gamma / r\), where \(\gamma\) is the surface tension. (As in Prob. 8.1, the last relation is the Laplace equation.)
9.4 Consider a gaseous mixture of \(4.0000 \times 10^{-2} \mathrm{~mol}\) of \(\mathrm{N}_{2}\) (A) and \(4.0000 \times 10^{-2} \mathrm{~mol}\) of \(\mathrm{CO}_{2}\) (B) in a volume of \(1.0000 \times 10^{-3} \mathrm{~m}^{3}\) at a temperature of \(298.15 \mathrm{~K}\). The second virial coefficients at this temperature have the values \({ }^{14}\)
\[
\begin{aligned}
B_{\mathrm{AA}} &=-4.8 \times 10^{-6} \mathrm{~m}^{3} \mathrm{~mol}^{-1} \\
B_{\mathrm{BB}} &=-124.5 \times 10^{-6} \mathrm{~m}^{3} \mathrm{~mol}^{-1} \\
B_{\mathrm{AB}} &=-47.5 \times 10^{-6} \mathrm{~m}^{3} \mathrm{~mol}^{-1}
\end{aligned}
\]
Compare the pressure of the real gas mixture with that predicted by the ideal gas equation. See Eqs. 9.3.20 and 9.3.23.
\({ }^{14}\) Refs. [3], [49], and [50].
9.5 At \(25^{\circ} \mathrm{C}\) and 1 bar, the Henry's law constants of nitrogen and oxygen dissolved in water are \(k_{\mathrm{H}, \mathrm{N}_{2}}=8.64 \times 10^{4}\) bar and \(k_{\mathrm{H}, \mathrm{O}_{2}}=4.41 \times 10^{4}\) bar. \({ }^{15}\) The vapor pressure of water at this temperature and pressure is \(p_{\mathrm{H}_{2} \mathrm{O}}=0.032\) bar. Assume that dry air contains only \(\mathrm{N}_{2}\) and \(\mathrm{O}_{2}\) at mole fractions \(y_{\mathrm{N}_{2}}=0.788\) and \(y_{\mathrm{O}_{2}}=0.212\). Consider liquid-gas systems formed by equilibrating liquid water and air at \(25^{\circ} \mathrm{C}\) and \(1.000 \mathrm{bar}\), and assume that the gas phase behaves as an ideal gas mixture.
Hint: The sum of the partial pressures of \(\mathrm{N}_{2}\) and \(\mathrm{O}_{2}\) must be \((1.000-0.032)\) bar \(=0.968\) bar. If the volume of one of the phases is much larger than that of the other, then almost all of the \(\mathrm{N}_{2}\) and \(\mathrm{O}_{2}\) will be in the predominant phase and the ratio of their amounts in this phase must be practically the same as in dry air.
Determine the mole fractions of \(\mathrm{N}_{2}\) and \(\mathrm{O}_{2}\) in both phases in the following limiting cases:
(a) A large volume of air is equilibrated with just enough water to leave a small drop of liquid.
(b) A large volume of water is equilibrated with just enough air to leave a small bubble of gas.
9.6 Derive the expression for \(\gamma_{m, \mathrm{~B}}\) given in Table 9.4, starting with Eq. 9.5.18.
9.7 Consider a nonideal binary gas mixture with the simple equation of state \(V=n R T / p+n B\) (Eq. \(9.3 .21\) ).
(a) The rule of Lewis and Randall states that the value of the mixed second virial coefficient \(B_{\mathrm{AB}}\) is the average of \(B_{\mathrm{AA}}\) and \(B_{\mathrm{BB}}\). Show that when this rule holds, the fugacity coefficient of \(\mathrm{A}\) in a binary gas mixture of any composition is given by \(\ln \phi_{\mathrm{A}}=B_{\mathrm{AA}} p / R T\). By comparing this expression with Eq. \(7.8 .18\) for a pure gas, express the fugacity of \(\mathrm{A}\) in the mixture as a function of the fugacity of pure \(A\) at the same temperature and pressure as the mixture.
(b) The rule of Lewis and Randall is not accurately obeyed when constituents A and B are chemically dissimilar. For example, at \(298.15 \mathrm{~K}\), the second virial coefficients of \(\mathrm{H}_{2} \mathrm{O}\) (A) and \(\mathrm{N}_{2}\) (B) are \(B_{\mathrm{AA}}=-1158 \mathrm{~cm}^{3} \mathrm{~mol}^{-1}\) and \(B_{\mathrm{BB}}=-5 \mathrm{~cm}^{3} \mathrm{~mol}^{-1}\), respectively, whereas the mixed second virial coefficient is \(B_{\mathrm{AB}}=-40 \mathrm{~cm}^{3} \mathrm{~mol}^{-1}\).
When liquid water is equilibrated with nitrogen at \(298.15 \mathrm{~K}\) and 1 bar, the partial pressure of \(\mathrm{H}_{2} \mathrm{O}\) in the gas phase is \(p_{\mathrm{A}}=0.03185\) bar. Use the given values of \(B_{\mathrm{AA}}, B_{\mathrm{BB}}\), and \(B_{\mathrm{AB}}\) to calculate the fugacity of the gaseous \(\mathrm{H}_{2} \mathrm{O}\) in this binary mixture. Compare this fugacity with the fugacity calculated with the value of \(B_{\mathrm{AB}}\) predicted by the rule of Lewis and Randall.
Table \(9.8\) Activity coefficient of benzene (A) in mixtures of benzene and 1 -octanol at \(20^{\circ} \mathrm{C}\). The reference state
is the pure liquid.
\begin{tabular}{lccc}
\hline\(x_{\mathrm{A}}\) & \(\gamma_{\mathrm{A}}\) & \(x_{\mathrm{A}}\) & \(\gamma_{\mathrm{A}}\) \\
\hline 0 & \(2.0^{a}\) & \(0.7631\) & \(1.183\) \\
\(0.1334\) & \(1.915\) & \(0.8474\) & \(1.101\) \\
\(0.2381\) & \(1.809\) & \(0.9174\) & \(1.046\) \\
\(0.4131\) & \(1.594\) & \(0.9782\) & \(1.005\) \\
\(0.5805\) & \(1.370\) & & \\
\hline \multicolumn{3}{l}{\(a_{\text {extrapolated }}\)}
\end{tabular}
\({ }^{15}\) Ref. [184].
9.8 Benzene and 1-octanol are two liquids that mix in all proportions. Benzene has a measurable vapor pressure, whereas 1-octanol is practically nonvolatile. The data in Table \(9.8\) on the preceding page were obtained by Platford \({ }^{16}\) using the isopiestic vapor pressure method.
(a) Use numerical integration to evaluate the integral on the right side of Eq. \(9.6 .10\) at each of the values of \(x_{\mathrm{A}}\) listed in the table, and thus find \(\gamma_{\mathrm{B}}\) at these compositions.
(b) Draw two curves on the same graph showing the effective mole fractions \(\gamma_{\mathrm{A}} x_{\mathrm{A}}\) and \(\gamma_{\mathrm{B}} x_{\mathrm{B}}\) as functions of \(x_{\mathrm{A}}\). Are the deviations from ideal-mixture behavior positive or negative?
Table \(9.9\) Liquid and gas compositions in the two-phase system of methanol (A) and benzene (B) at \(45^{\circ} \mathrm{C}^{a}\)
\begin{tabular}{llllll}
\hline\(x_{\mathrm{A}}\) & \(y_{\mathrm{A}}\) & \(p / \mathrm{kPa}\) & \(x_{\mathrm{A}}\) & \(y_{\mathrm{A}}\) & \(p / \mathrm{kPa}\) \\
\hline 0 & 0 & \(29.894\) & \(0.4201\) & \(0.5590\) & \(60.015\) \\
\(0.0207\) & \(0.2794\) & \(40.962\) & \(0.5420\) & \(0.5783\) & \(60.416\) \\
\(0.0314\) & \(0.3391\) & \(44.231\) & \(0.6164\) & \(0.5908\) & \(60.416\) \\
\(0.0431\) & \(0.3794\) & \(46.832\) & \(0.7259\) & \(0.6216\) & \(59.868\) \\
\(0.0613\) & \(0.4306\) & \(50.488\) & \(0.8171\) & \(0.6681\) & \(58.321\) \\
\(0.0854\) & \(0.4642\) & \(53.224\) & \(0.9033\) & \(0.7525\) & \(54.692\) \\
\(0.1811\) & \(0.5171\) & \(57.454\) & \(0.9497\) & \(0.8368\) & \(51.009\) \\
\(0.3217\) & \(0.5450\) & \(59.402\) & 1 & 1 & \(44.608\) \\
\hline
\end{tabular}
\({ }^{a}\) Ref. [169].
9.9 Table \(9.9\) lists measured values of gas-phase composition and total pressure for the binary two-phase methanol-benzene system at constant temperature and varied liquid-phase composition. \(x_{\mathrm{A}}\) is the mole fraction of methanol in the liquid mixture, and \(y_{\mathrm{A}}\) is the mole fraction of methanol in the equilibrated gas phase.
(a) For each of the 16 different liquid-phase compositions, tabulate the partial pressures of \(\mathrm{A}\) and \(\mathrm{B}\) in the equilibrated gas phase.
(b) Plot \(p_{\mathrm{A}}\) and \(p_{\mathrm{B}}\) versus \(x_{\mathrm{A}}\) on the same graph. Notice that the behavior of the mixture is far from that of an ideal mixture. Are the deviations from Raoult's law positive or negative?
(c) Tabulate and plot the activity coefficient \(\gamma_{\mathrm{B}}\) of the benzene as a function of \(x_{\mathrm{A}}\) using a pure-liquid reference state. Assume that the fugacity \(f_{\mathrm{B}}\) is equal to \(p_{\mathrm{B}}\), and ignore the effects of variable pressure.
(d) Estimate the Henry's law constant \(k_{\mathrm{H}, \mathrm{A}}\) of methanol in the benzene environment at \(45^{\circ} \mathrm{C}\) by the graphical method suggested in Fig. 9.7(b). Again assume that \(f_{\mathrm{A}}\) and \(p_{\mathrm{A}}\) are equal, and ignore the effects of variable pressure.
9.10 Consider a dilute binary nonelectrolyte solution in which the dependence of the chemical potential of solute B on composition is given by
\[
\mu_{\mathrm{B}}=\mu_{m, \mathrm{~B}}^{\mathrm{ref}}+R T \ln \frac{m_{\mathrm{B}}}{m^{\circ}}+k_{m} m_{\mathrm{B}}
\]
where \(\mu_{m, \mathrm{~B}}^{\mathrm{ref}}\) and \(k_{m}\) are constants at a given \(T\) and \(p\). (The derivation of this equation is sketched in Sec. 9.5.4.) Use the Gibbs-Duhem equation in the form \(\mathrm{d} \mu_{\mathrm{A}}=-\left(n_{\mathrm{B}} / n_{\mathrm{A}}\right) \mathrm{d} \mu_{\mathrm{B}}\) to obtain an expression for \(\mu_{\mathrm{A}}-\mu_{\mathrm{A}}^{*}\) as a function of \(m_{\mathrm{B}}\) in this solution.
\({ }^{16}\) Ref. [145].
9.11 By means of the isopiestic vapor pressure technique, the osmotic coefficients of aqueous solutions of urea at \(25^{\circ} \mathrm{C}\) have been measured at molalities up to the saturation limit of about \(20 \mathrm{~mol} \mathrm{~kg}^{-1} .{ }^{17}\) The experimental values are closely approximated by the function
\[
\phi_{m}=1.00-\frac{0.050 m_{\mathrm{B}} / m^{\circ}}{1.00+0.179 m_{\mathrm{B}} / m^{\circ}}
\]
where \(m^{\circ}\) is \(1 \mathrm{~mol} \mathrm{~kg}^{-1}\). Calculate values of the solvent and solute activity coefficients \(\gamma_{\mathrm{A}}\) and \(\gamma_{m, \mathrm{~B}}\) at various molalities in the range \(0-20 \mathrm{~mol} \mathrm{~kg}^{-1}\), and plot them versus \(m_{\mathrm{B}} / m^{\circ}\). Use enough points to be able to see the shapes of the curves. What are the limiting slopes of these curves as \(m_{\mathrm{B}}\) approaches zero?
9.12 Use Eq. \(9.2 .49\) to derive an expression for the rate at which the logarithm of the activity coefficient of component \(i\) of a liquid mixture changes with pressure at constant temperature and composition: \(\left(\partial \ln \gamma_{i} / \partial p\right)_{T,\left\{n_{i}\right\}}=\) ?
9.13 Assume that at sea level the atmosphere has a pressure of \(1.00\) bar and a composition given by \(y_{\mathrm{N}_{2}}=0.788\) and \(y_{\mathrm{O}_{2}}=0.212\). Find the partial pressures and mole fractions of \(\mathrm{N}_{2}\) and \(\mathrm{O}_{2}\), and the total pressure, at an altitude of \(10.0 \mathrm{~km}\), making the (drastic) approximation that the atmosphere is an ideal gas mixture in an equilibrium state at \(0^{\circ} \mathrm{C}\). For \(g\) use the value of the standard acceleration of free fall listed in Appendix B.
9.14 Consider a tall column of a dilute binary liquid solution at equilibrium in a gravitational field.
(a) Derive an expression for \(\ln \left[c_{\mathrm{B}}(h) / c_{\mathrm{B}}(0)\right]\), where \(c_{\mathrm{B}}(h)\) and \(c_{\mathrm{B}}(0)\) are the solute concentrations at elevations \(h\) and 0 . Your expression should be a function of \(h, M_{\mathrm{B}}, T, \rho\), and the partial specific volume of the solute at infinite dilution, \(v_{\mathrm{B}}^{\infty}\). For the dependence of pressure on elevation, you may use the hydrostatic formula \(\mathrm{d} p=-\rho g \mathrm{~d} h\) (Eq. \(8.1 .14\) on page 200) and assume the solution density \(\rho\) is the same at all elevations. Hint: use the derivation leading to Eq. \(9.8 .22\) as a guide.
(b) Suppose you have a tall vessel containing a dilute solution of a macromolecule solute of molar mass \(M_{\mathrm{B}}=10.0 \mathrm{~kg} \mathrm{~mol}^{-1}\) and partial specific volume \(v_{\mathrm{B}}^{\infty}=0.78 \mathrm{~cm}^{3} \mathrm{~g}^{-1}\). The solution density is \(\rho=1.00 \mathrm{~g} \mathrm{~cm}^{-3}\) and the temperature is \(T=300 \mathrm{~K}\). Find the height \(h\) from the bottom of the vessel at which, in the equilibrium state, the concentration \(c_{\mathrm{B}}\) has decreased to 99 percent of the concentration at the bottom.
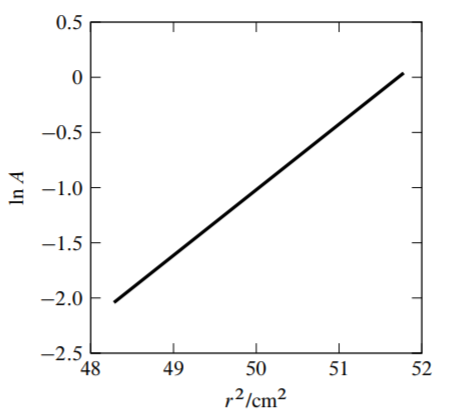
9.15 FhuA is a protein found in the outer membrane of the Escherichia coli bacterium. From the known amino acid sequence, its molar mass is calculated to be \(78.804 \mathrm{~kg} \mathrm{~mol}^{-1}\). In aqueous solution, molecules of the detergent dodecyl maltoside bind to a FhuA molecule to form an aggregate that behaves as a single solute species. Figure \(9.13\) on the next page shows data collected in a sedimentation equilibrium experiment with a dilute solution of the aggregate. \({ }^{18}\) In the graph, \(A\) is the absorbance measured at a wavelength of \(280 \mathrm{~nm}\) (a property that is a linear function of the aggregate concentration) and \(r\) is the radial distance from the axis of rotation of the centrifuge rotor. The experimental points fall very close to the straight line shown in the graph. The sedimentation conditions were \(\omega=838 \mathrm{~s}^{-1}\) and \(T=293 \mathrm{~K}\). The authors used the values \(v_{\mathrm{B}}^{\infty}=0.776 \mathrm{~cm}^{3} \mathrm{~g}^{-1}\) and \(\rho=1.004 \mathrm{~g} \mathrm{~cm}^{-3}\).
(a) The values of \(r\) at which the absorbance was measured range from \(6.95 \mathrm{~cm}\) to \(7.20 \mathrm{~cm}\). Find the difference of pressure in the solution between these two positions.
(b) Find the molar mass of the aggregate solute species, and use it to estimate the mass binding ratio (the mass of bound detergent divided by the mass of protein).
\({ }^{17}\) Ref. [160]. \({ }^{18}\) Ref. [18].