8.2: Phase Diagrams of Pure Substances
- Page ID
- 20608
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
\( \newcommand{\tx}[1]{\text{#1}} % text in math mode\)
\( \newcommand{\subs}[1]{_{\text{#1}}} % subscript text\)
\( \newcommand{\sups}[1]{^{\text{#1}}} % superscript text\)
\( \newcommand{\st}{^\circ} % standard state symbol\)
\( \newcommand{\id}{^{\text{id}}} % ideal\)
\( \newcommand{\rf}{^{\text{ref}}} % reference state\)
\( \newcommand{\units}[1]{\mbox{$\thinspace$#1}}\)
\( \newcommand{\K}{\units{K}} % kelvins\)
\( \newcommand{\degC}{^\circ\text{C}} % degrees Celsius\)
\( \newcommand{\br}{\units{bar}} % bar (\bar is already defined)\)
\( \newcommand{\Pa}{\units{Pa}}\)
\( \newcommand{\mol}{\units{mol}} % mole\)
\( \newcommand{\V}{\units{V}} % volts\)
\( \newcommand{\timesten}[1]{\mbox{$\,\times\,10^{#1}$}}\)
\( \newcommand{\per}{^{-1}} % minus one power\)
\( \newcommand{\m}{_{\text{m}}} % subscript m for molar quantity\)
\( \newcommand{\CVm}{C_{V,\text{m}}} % molar heat capacity at const.V\)
\( \newcommand{\Cpm}{C_{p,\text{m}}} % molar heat capacity at const.p\)
\( \newcommand{\kT}{\kappa_T} % isothermal compressibility\)
\( \newcommand{\A}{_{\text{A}}} % subscript A for solvent or state A\)
\( \newcommand{\B}{_{\text{B}}} % subscript B for solute or state B\)
\( \newcommand{\bd}{_{\text{b}}} % subscript b for boundary or boiling point\)
\( \newcommand{\C}{_{\text{C}}} % subscript C\)
\( \newcommand{\f}{_{\text{f}}} % subscript f for freezing point\)
\( \newcommand{\mA}{_{\text{m},\text{A}}} % subscript m,A (m=molar)\)
\( \newcommand{\mB}{_{\text{m},\text{B}}} % subscript m,B (m=molar)\)
\( \newcommand{\mi}{_{\text{m},i}} % subscript m,i (m=molar)\)
\( \newcommand{\fA}{_{\text{f},\text{A}}} % subscript f,A (for fr. pt.)\)
\( \newcommand{\fB}{_{\text{f},\text{B}}} % subscript f,B (for fr. pt.)\)
\( \newcommand{\xbB}{_{x,\text{B}}} % x basis, B\)
\( \newcommand{\xbC}{_{x,\text{C}}} % x basis, C\)
\( \newcommand{\cbB}{_{c,\text{B}}} % c basis, B\)
\( \newcommand{\mbB}{_{m,\text{B}}} % m basis, B\)
\( \newcommand{\kHi}{k_{\text{H},i}} % Henry's law constant, x basis, i\)
\( \newcommand{\kHB}{k_{\text{H,B}}} % Henry's law constant, x basis, B\)
\( \newcommand{\arrow}{\,\rightarrow\,} % right arrow with extra spaces\)
\( \newcommand{\arrows}{\,\rightleftharpoons\,} % double arrows with extra spaces\)
\( \newcommand{\ra}{\rightarrow} % right arrow (can be used in text mode)\)
\( \newcommand{\eq}{\subs{eq}} % equilibrium state\)
\( \newcommand{\onehalf}{\textstyle\frac{1}{2}\D} % small 1/2 for display equation\)
\( \newcommand{\sys}{\subs{sys}} % system property\)
\( \newcommand{\sur}{\sups{sur}} % surroundings\)
\( \renewcommand{\in}{\sups{int}} % internal\)
\( \newcommand{\lab}{\subs{lab}} % lab frame\)
\( \newcommand{\cm}{\subs{cm}} % center of mass\)
\( \newcommand{\rev}{\subs{rev}} % reversible\)
\( \newcommand{\irr}{\subs{irr}} % irreversible\)
\( \newcommand{\fric}{\subs{fric}} % friction\)
\( \newcommand{\diss}{\subs{diss}} % dissipation\)
\( \newcommand{\el}{\subs{el}} % electrical\)
\( \newcommand{\cell}{\subs{cell}} % cell\)
\( \newcommand{\As}{A\subs{s}} % surface area\)
\( \newcommand{\E}{^\mathsf{E}} % excess quantity (superscript)\)
\( \newcommand{\allni}{\{n_i \}} % set of all n_i\)
\( \newcommand{\sol}{\hspace{-.1em}\tx{(sol)}}\)
\( \newcommand{\solmB}{\tx{(sol,$\,$$m\B$)}}\)
\( \newcommand{\dil}{\tx{(dil)}}\)
\( \newcommand{\sln}{\tx{(sln)}}\)
\( \newcommand{\mix}{\tx{(mix)}}\)
\( \newcommand{\rxn}{\tx{(rxn)}}\)
\( \newcommand{\expt}{\tx{(expt)}}\)
\( \newcommand{\solid}{\tx{(s)}}\)
\( \newcommand{\liquid}{\tx{(l)}}\)
\( \newcommand{\gas}{\tx{(g)}}\)
\( \newcommand{\pha}{\alpha} % phase alpha\)
\( \newcommand{\phb}{\beta} % phase beta\)
\( \newcommand{\phg}{\gamma} % phase gamma\)
\( \newcommand{\aph}{^{\alpha}} % alpha phase superscript\)
\( \newcommand{\bph}{^{\beta}} % beta phase superscript\)
\( \newcommand{\gph}{^{\gamma}} % gamma phase superscript\)
\( \newcommand{\aphp}{^{\alpha'}} % alpha prime phase superscript\)
\( \newcommand{\bphp}{^{\beta'}} % beta prime phase superscript\)
\( \newcommand{\gphp}{^{\gamma'}} % gamma prime phase superscript\)
\( \newcommand{\apht}{\small\aph} % alpha phase tiny superscript\)
\( \newcommand{\bpht}{\small\bph} % beta phase tiny superscript\)
\( \newcommand{\gpht}{\small\gph} % gamma phase tiny superscript\)
\( \newcommand{\upOmega}{\Omega}\)
\( \newcommand{\dif}{\mathop{}\!\mathrm{d}} % roman d in math mode, preceded by space\)
\( \newcommand{\Dif}{\mathop{}\!\mathrm{D}} % roman D in math mode, preceded by space\)
\( \newcommand{\df}{\dif\hspace{0.05em} f} % df\)
\(\newcommand{\dBar}{\mathop{}\!\mathrm{d}\hspace-.3em\raise1.05ex{\Rule{.8ex}{.125ex}{0ex}}} % inexact differential \)
\( \newcommand{\dq}{\dBar q} % heat differential\)
\( \newcommand{\dw}{\dBar w} % work differential\)
\( \newcommand{\dQ}{\dBar Q} % infinitesimal charge\)
\( \newcommand{\dx}{\dif\hspace{0.05em} x} % dx\)
\( \newcommand{\dt}{\dif\hspace{0.05em} t} % dt\)
\( \newcommand{\difp}{\dif\hspace{0.05em} p} % dp\)
\( \newcommand{\Del}{\Delta}\)
\( \newcommand{\Delsub}[1]{\Delta_{\text{#1}}}\)
\( \newcommand{\pd}[3]{(\partial #1 / \partial #2 )_{#3}} % \pd{}{}{} - partial derivative, one line\)
\( \newcommand{\Pd}[3]{\left( \dfrac {\partial #1} {\partial #2}\right)_{#3}} % Pd{}{}{} - Partial derivative, built-up\)
\( \newcommand{\bpd}[3]{[ \partial #1 / \partial #2 ]_{#3}}\)
\( \newcommand{\bPd}[3]{\left[ \dfrac {\partial #1} {\partial #2}\right]_{#3}}\)
\( \newcommand{\dotprod}{\small\bullet}\)
\( \newcommand{\fug}{f} % fugacity\)
\( \newcommand{\g}{\gamma} % solute activity coefficient, or gamma in general\)
\( \newcommand{\G}{\varGamma} % activity coefficient of a reference state (pressure factor)\)
\( \newcommand{\ecp}{\widetilde{\mu}} % electrochemical or total potential\)
\( \newcommand{\Eeq}{E\subs{cell, eq}} % equilibrium cell potential\)
\( \newcommand{\Ej}{E\subs{j}} % liquid junction potential\)
\( \newcommand{\mue}{\mu\subs{e}} % electron chemical potential\)
\( \newcommand{\defn}{\,\stackrel{\mathrm{def}}{=}\,} % "equal by definition" symbol\)
\( \newcommand{\D}{\displaystyle} % for a line in built-up\)
\( \newcommand{\s}{\smash[b]} % use in equations with conditions of validity\)
\( \newcommand{\cond}[1]{\\[-2.5pt]{}\tag*{#1}}\)
\( \newcommand{\nextcond}[1]{\\[-5pt]{}\tag*{#1}}\)
\( \newcommand{\R}{8.3145\units{J$\,$K$\per\,$mol$\per$}} % gas constant value\)
\( \newcommand{\Rsix}{8.31447\units{J$\,$K$\per\,$mol$\per$}} % gas constant value - 6 sig figs\)
\( \newcommand{\jn}{\hspace3pt\lower.3ex{\Rule{.6pt}{2ex}{0ex}}\hspace3pt} \)
\( \newcommand{\ljn}{\hspace3pt\lower.3ex{\Rule{.6pt}{.5ex}{0ex}}\hspace-.6pt\raise.45ex{\Rule{.6pt}{.5ex}{0ex}}\hspace-.6pt\raise1.2ex{\Rule{.6pt}{.5ex}{0ex}} \hspace3pt} \)
\( \newcommand{\lljn}{\hspace3pt\lower.3ex{\Rule{.6pt}{.5ex}{0ex}}\hspace-.6pt\raise.45ex{\Rule{.6pt}{.5ex}{0ex}}\hspace-.6pt\raise1.2ex{\Rule{.6pt}{.5ex}{0ex}}\hspace1.4pt\lower.3ex{\Rule{.6pt}{.5ex}{0ex}}\hspace-.6pt\raise.45ex{\Rule{.6pt}{.5ex}{0ex}}\hspace-.6pt\raise1.2ex{\Rule{.6pt}{.5ex}{0ex}}\hspace3pt} \)
A phase diagram is a two-dimensional map showing which phase or phases are able to exist in an equilibrium state under given conditions. This chapter describes pressure–volume and pressure–temperature phase diagrams for a single substance, and Chap. 13 will describe numerous types of phase diagrams for multicomponent systems.
8.2.1 Features of phase diagrams
Two-dimensional phase diagrams for a single-substance system can be generated as projections of a three-dimensional surface in a coordinate system with Cartesian axes \(p\), \(V/n\), and \(T\). A point on the three-dimensional surface corresponds to a physically-realizable combination of values, for an equilibrium state of the system containing a total amount \(n\) of the substance, of the variables \(p\), \(V/n\), and \(T\).
The concepts needed to interpret single-substance phase diagrams will be illustrated with carbon dioxide.
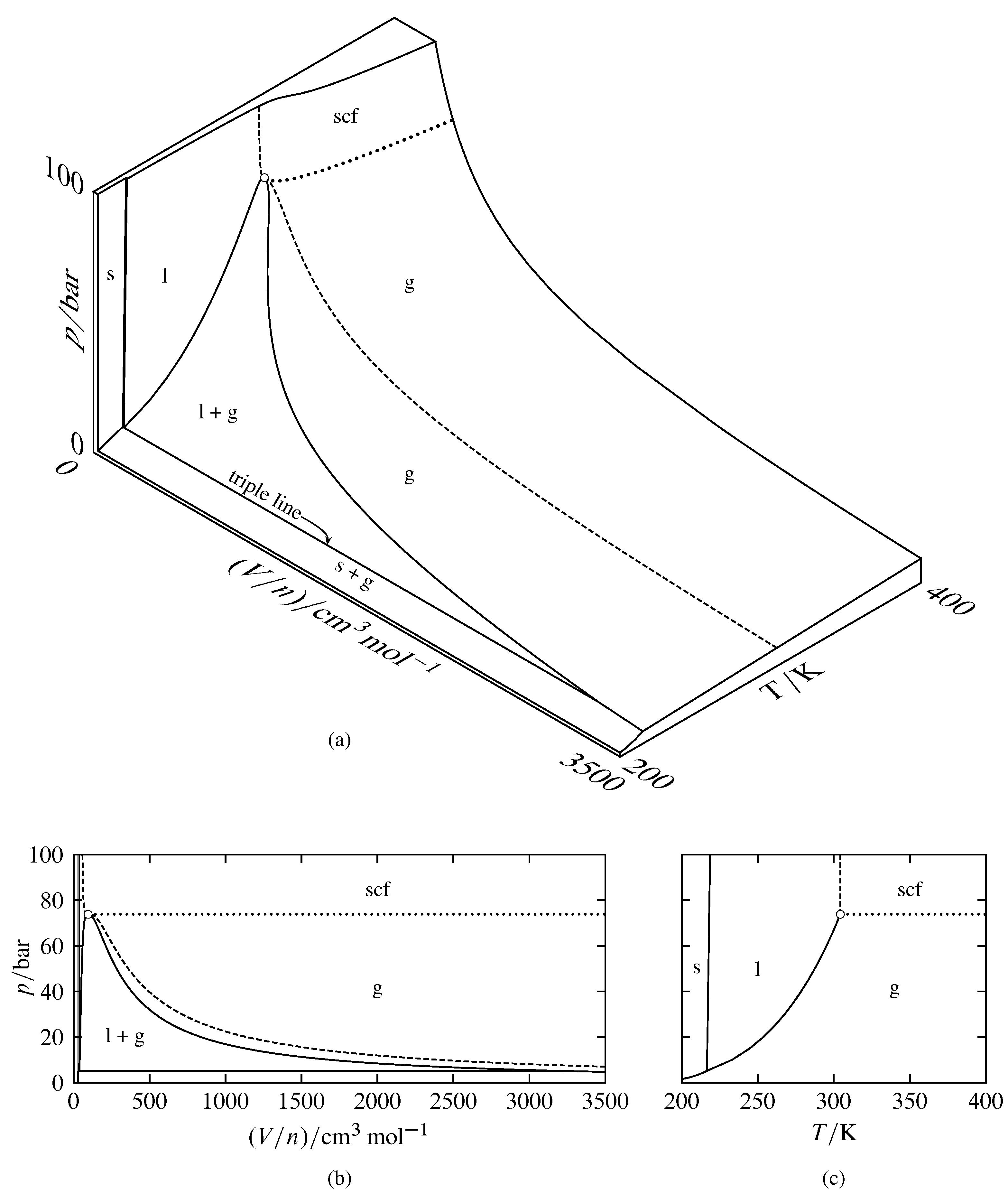
Figure 8.2 Relations among \(p\), \(V/n\), and \(T\) for carbon dioxide (based on data in NIST Chemistry WebBook and in S. Angus, B. Armstrong, and K. M. de Reuck, International Thermodynamic Tables of the Fluid State, Vol. 3, Carbon Dioxide, Pergamon Press, Oxford, 1976). Areas are labeled with the stable phase or phases (scf stands for supercritical fluid). The open circle indicates the critical point.
(a) Three-dimensional \(p\)–\((V/n)\)–\(T\) surface. The dashed curve is the critical isotherm at \(T=304.21\K\), and the dotted curve is a portion of the critical isobar at \(p=73.8\br\).
(b) Pressure–volume phase diagram (projection of the surface onto the \(p\)–\((V/n)\) plane).
(c) Pressure–temperature phase diagram (projection of the surface onto the \(p\)–\(T\) plane).
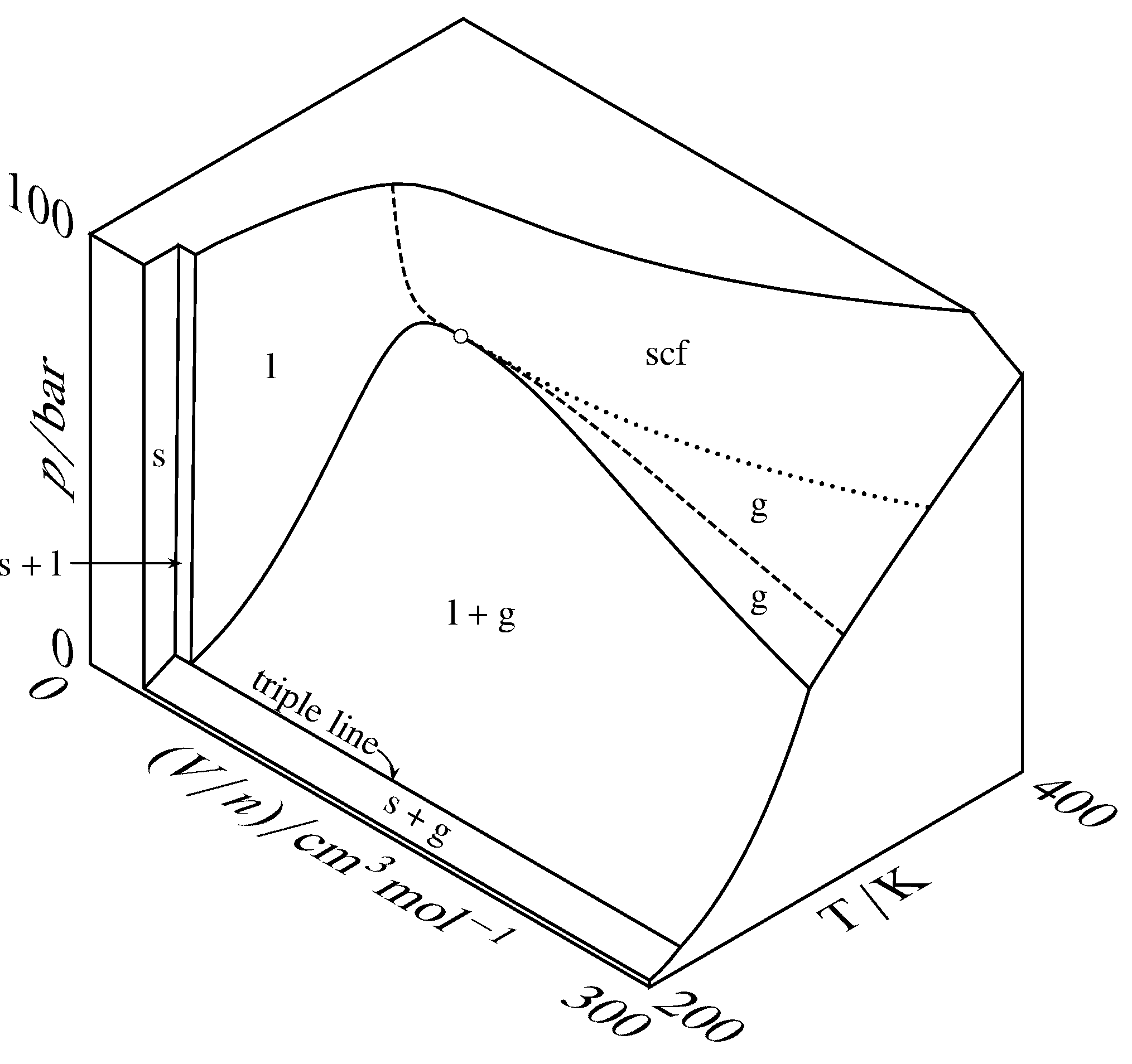
Figure 8.3 Three-dimensional \(p\)–\((V/n)\)–\(T\) surface for CO\(_2\), magnified along the \(V/n\) axis compared to Fig. 8.2. The open circle is the critical point, the dashed curve is the critical isotherm, and the dotted curve is a portion of the critical isobar.
Three-dimensional surfaces for carbon dioxide are shown at two different scales in Fig. 8.2 and in Fig. 8.3. In these figures, some areas of the surface are labeled with a single physical state: solid, liquid, gas, or supercritical fluid. A point in one of these areas corresponds to an equilibrium state of the system containing a single phase of the labeled physical state. The shape of the surface in this one-phase area gives the equation of state of the phase (i.e., the dependence of one of the variables on the other two). A point in an area labeled with two physical states corresponds to two coexisting phases. The triple line is the locus of points for all possible equilibrium systems of three coexisting phases, which in this case are solid, liquid, and gas. A point on the triple line can also correspond to just one or two phases.
The two-dimensional projections shown in Figs. 8.2(b) and 8.2(c) are pressure–volume and pressure–temperature phase diagrams. Because all phases of a multiphase equilibrium system have the same temperature and pressure (assuming there are no constraints such as internal adiabatic partitions), the projection of each two-phase area onto the pressure–temperature diagram is a curve, called a coexistence curve or phase boundary, and the projection of the triple line is a point, called a triple point.
How may we use a phase diagram? The two axes represent values of two independent variables, such as \(p\) and \(V/n\) or \(p\) and \(T\). For given values of these variables, we place a point on the diagram at the intersection of the corresponding coordinates; this is the system point. Then depending on whether the system point falls in an area or on a coexistence curve, the diagram tells us the number and kinds of phases that can be present in the equilibrium system.
If the system point falls within an area labeled with the physical state of a single phase, only that one kind of phase can be present in the equilibrium system. A system containing a pure substance in a single phase is bivariant (\(F = 3 - 1 = 2\)), so we may vary two intensive properties independently. That is, the system point may move independently along two coordinates (\(p\) and \(V/n\), or \(p\) and \(T\)) and still remain in the one-phase area of the phase diagram. When \(V\) and \(n\) refer to a single phase, the variable \(V/n\) is the molar volume \(V\m\) in the phase.
If the system point falls in an area of the pressure–volume phase diagram labeled with symbols for two phases, these two phases coexist in equilibrium. The phases have the same pressure and different molar volumes. To find the molar volumes of the individual phases, we draw a horizontal line of constant pressure, called a tie line, through the system point and extending from one edge of the area to the other. The horizontal position of each end of the tie line, where it terminates at the boundary with a one-phase area, gives the molar volume in that phase in the two-phase system. For an example of a tie line, see Fig. 8.9.
The triple line on the pressure–volume diagram represents the range of values of \(V/n\) in which three phases (solid, liquid, and gas) can coexist at equilibrium.
Helium is the only substance lacking a solid–liquid–gas triple line. When a system containing the coexisting liquid and gas of \({}^4\)He is cooled to \(2.17\K\), a triple point is reached in which the third phase is a liquid called He-II, which has the unique property of superfluidity. It is only at high pressures (\(10\br\) or greater) that solid helium can exist.
A three-phase one-component system is invariant (\(F = 3 - 3 = 0\)); there is only one temperature (the triple-point temperature \(T\subs{tp}\)) and one pressure (the triple-point pressure \(p\subs{tp}\)) at which the three phases can coexist. The values of \(T\subs{tp}\) and \(p\subs{tp}\) are unique to each substance, and are shown by the position of the triple point on the pressure–temperature phase diagram. The molar volumes in the three coexisting phases are given by the values of \(V/n\) at the three points on the pressure–volume diagram where the triple line touches a one-phase area. These points are at the two ends and an intermediate position of the triple line. If the system point is at either end of the triple line, only the one phase of corresponding molar volume at temperature \(T\subs{tp}\) and pressure \(p\subs{tp}\) can be present. When the system point is on the triple line anywhere between the two ends, either two or three phases can be present. If the system point is at the position on the triple line corresponding to the phase of intermediate molar volume, there might be only that one phase present.
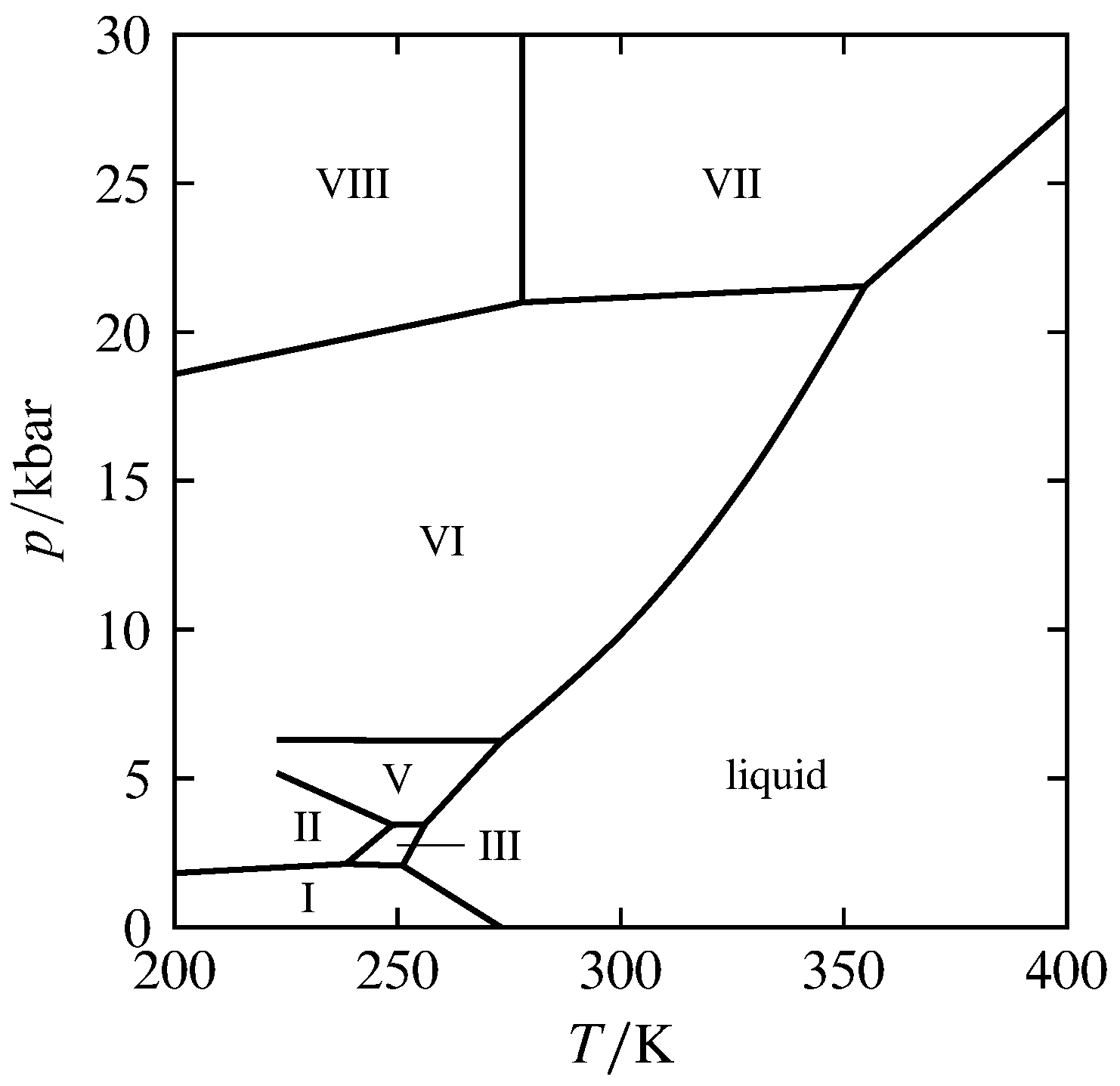
Figure 8.4 High-pressure pressure–temperature phase diagram of H\(_2\)O (based on data in D. Eisenberg and W. Kauzmann, The Structure and Properties of Water, Oxford University Press, New York, 1969, Table 3.5, and Carl W. F. T. Pistorius et al, J. Chem. Phys., 38, 600–602, 1963). The roman numerals designate seven forms of ice.
At high pressures, a substance may have additional triple points for two solid phases and the liquid, or for three solid phases. This is illustrated by the pressure–temperature phase diagram of H\(_2\)O in Fig. 8.4, which extends to pressures up to \(30\units{kbar}\). (On this scale, the liquid–gas coexistence curve lies too close to the horizontal axis to be visible.) The diagram shows seven different solid phases of H\(_2\)O differing in crystal structure and designated ice I, ice II, and so on. Ice I is the ordinary form of ice, stable below \(2\br\). On the diagram are four triple points for two solids and the liquid and three triple points for three solids. Each triple point is invariant. Note how H\(_2\)O can exist as solid ice VI or ice VII above its standard melting point of \(273\K\) if the pressure is high enough (“hot ice” ).
8.2.2 Two-phase equilibrium
A system containing two phases of a pure substance in equilibrium is univariant. Both phases have the same values of \(T\) and of \(p\), but these values are not independent because of the requirement that the phases have equal chemical potentials. We may vary only one intensive variable of a pure substance (such as \(T\) or \(p\)) independently while two phases coexist in equilibrium.
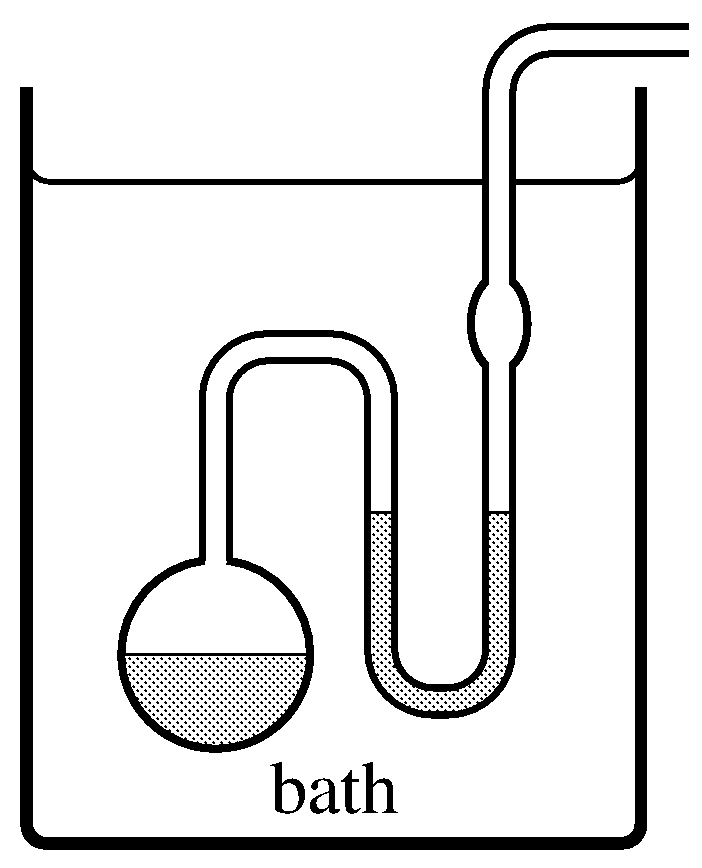
Figure 8.5 An isoteniscope. The liquid to be investigated is placed in the vessel and U-tube, as indicated by shading, and maintained at a fixed temperature in the bath. The pressure in the side tube is reduced until the liquid boils gently and its vapor sweeps out the air. The pressure is adjusted until the liquid level is the same in both limbs of the U-tube; the vapor pressure of the liquid is then equal to the pressure in the side tube, which can be measured with a manometer.
At a given temperature, the pressure at which solid and gas or liquid and gas are in equilibrium is called the vapor pressure or saturation vapor pressure of the solid or liquid. The vapor pressure of a solid is sometimes called the sublimation pressure. We may measure the vapor pressure of a liquid at a fixed temperature with a simple device called an isoteniscope (Fig. 8.5).
In a system of more than one substance, vapor pressure can refer to the partial pressure of a substance in a gas mixture equilibrated with a solid or liquid of that substance. The effect of total pressure on vapor pressure will be discussed in Sec. 12.8.1. This e-book refers to the saturation vapor pressure of a liquid when it is necessary to indicate that it is the pure liquid and pure gas phases that are in equilibrium at the same pressure.
At a given pressure, the melting point or freezing point is the temperature at which solid and liquid are in equilibrium, the boiling point or saturation temperature is the temperature at which liquid and gas are in equilibrium, and the sublimation temperature or sublimation point is the temperature at which solid and gas are in equilibrium.
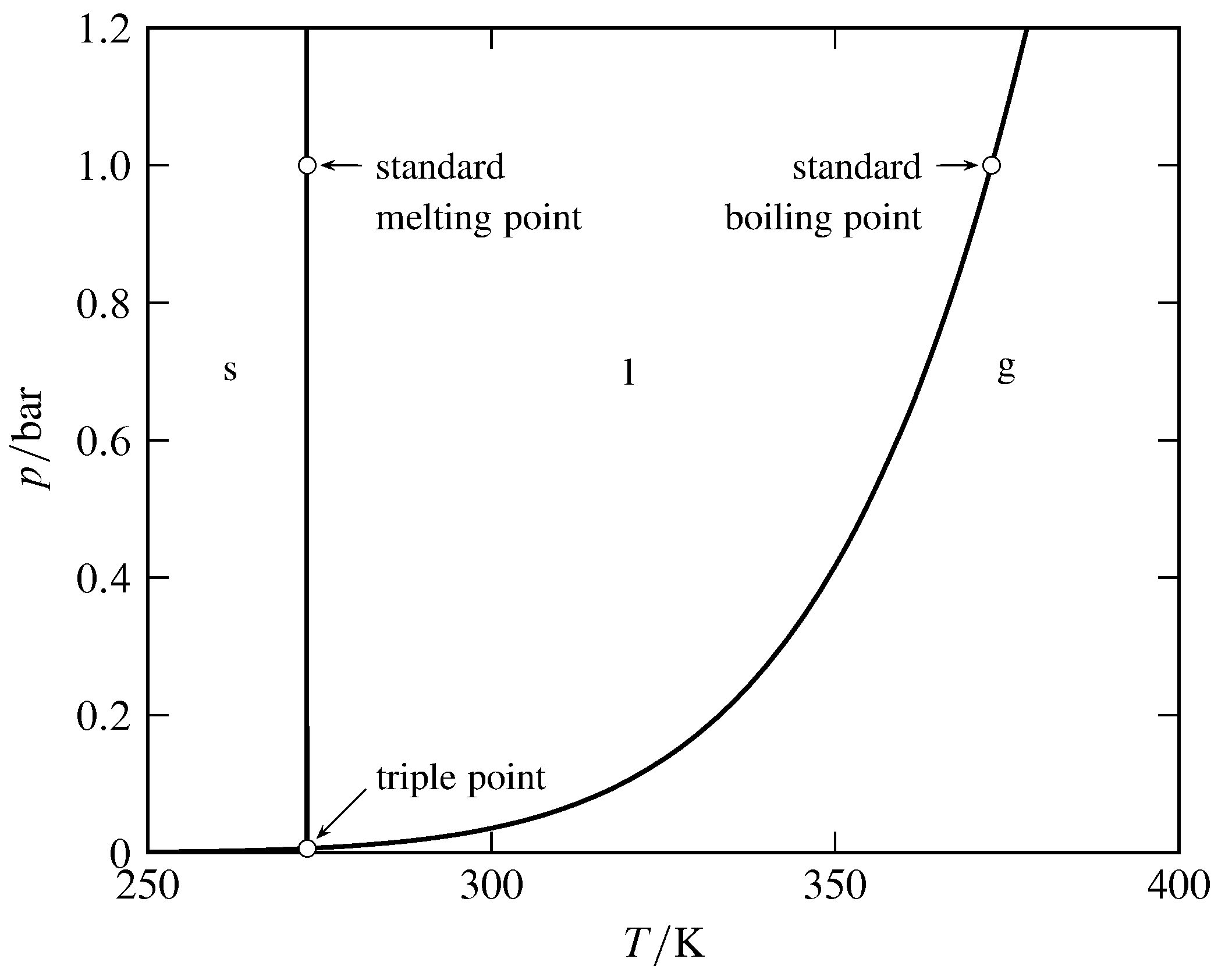
Figure 8.6 Pressure–temperature phase diagram of H\(_2\)O. (Based on data in NIST Chemistry WebBook.)
The relation between temperature and pressure in a system with two phases in equilibrium is shown by the coexistence curve separating the two one-phase areas on the pressure–temperature diagram (see Fig. 8.6). Consider the liquid–gas curve. If we think of \(T\) as the independent variable, the curve is a vapor-pressure curve showing how the vapor pressure of the liquid varies with temperature. If, however, \(p\) is the independent variable, then the curve is a boiling-point curve showing the dependence of the boiling point on pressure.
The normal melting point or boiling point refers to a pressure of one atmosphere, and the standard melting point or boiling point refers to the standard pressure. Thus, the normal boiling point of water (\(99.97\units{\(\degC\)}\)) is the boiling point at \(1\units{atm}\); this temperature is also known as the steam point. The standard boiling point of water (\(99.61\units{\(\degC\)}\)) is the boiling point at the slightly lower pressure of \(1\br\).
Coexistence curves will be discussed further in Sec. 8.4.
8.2.3 The critical point
Every substance has a certain temperature, the critical temperature, above which only one fluid phase can exist at any volume and pressure (Sec. 2.2.3). The critical point is the point on a phase diagram corresponding to liquid–gas coexistence at the critical temperature, and the critical pressure is the pressure at this point.

Figure 8.7 Glass bulb filled with CO\(_2\) at a value of \(V/n\) close to the critical value, viewed at four different temperatures. The three balls have densities less than, approximately equal to, and greater than the critical density. (Photos by permission of the photographer; they appeared in Jan V. Sengers and Anneke Levelt Sengers, Chem. Eng. News, June 10, 104–118, 1968.)
(a) Supercritical fluid at a temperature above the critical temperature.
(b) Intense opalescence just above the critical temperature.
(c) Meniscus formation slightly below the critical temperature; liquid and gas of nearly the same density.
(d) Temperature well below the critical temperature; liquid and gas of greatly different densities.
To observe the critical point of a substance experimentally, we can evacuate a glass vessel, introduce an amount of the substance such that \(V/n\) is approximately equal to the molar volume at the critical point, seal the vessel, and raise the temperature above the critical temperature. The vessel now contains a single fluid phase. When the substance is slowly cooled to a temperature slightly above the critical temperature, it exhibits a cloudy appearance, a phenomenon called critical opalescence (Fig. 8.7). The opalescence is the scattering of light caused by large local density fluctuations. At the critical temperature, a meniscus forms between liquid and gas phases of practically the same density. With further cooling, the density of the liquid increases and the density of the gas decreases.
At temperatures above the critical temperature and pressures above the critical pressure, the one existing fluid phase is called a supercritical fluid. Thus, a supercritical fluid of a pure substance is a fluid that does not undergo a phase transition to a different fluid phase when we change the pressure at constant temperature or change the temperature at constant pressure.
If, however, we increase \(p\) at constant \(T\), the supercritical fluid will change to a solid. In the phase diagram of H\(_2\)O, the coexistence curve for ice VII and liquid shown in Fig. 8.4 extends to a higher temperature than the critical temperature of \(647\K\). Thus, supercritical water can be converted to ice VII by isothermal compression.
A fluid in the supercritical region can have a density comparable to that of the liquid, and can be more compressible than the liquid. Under supercritical conditions, a substance is often an excellent solvent for solids and liquids. By varying the pressure or temperature, the solvating power can be changed; by reducing the pressure isothermally, the substance can be easily removed as a gas from dissolved solutes. These properties make supercritical fluids useful for chromatography and solvent extraction.
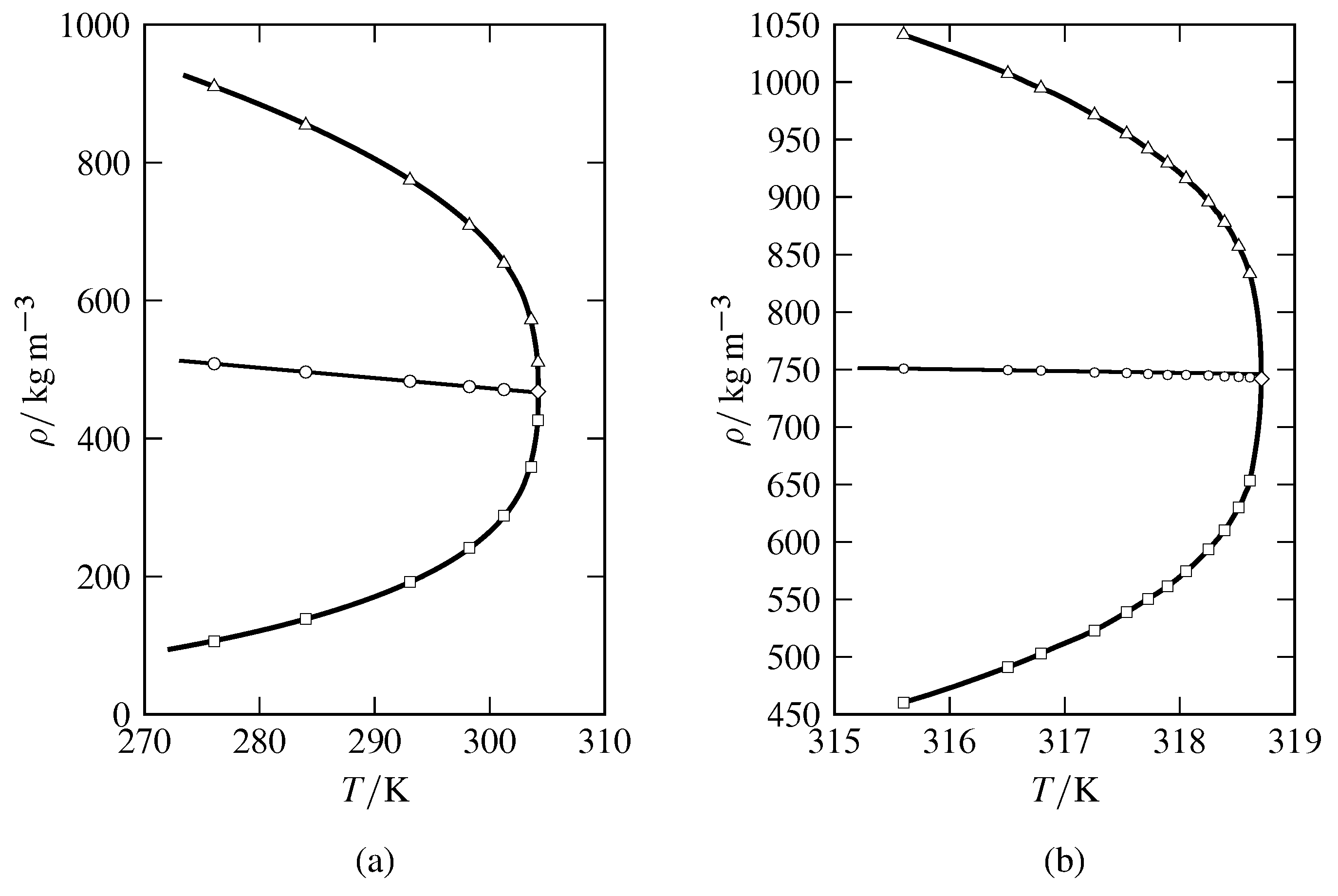
Figure 8.8 Densities of coexisting gas and liquid phases close to the critical point as functions of temperature for (a) CO\(_2\) (based on data in A. Michels, B. Blaisse, and C. Michels, Proc. R. Soc. London, Ser. A, 160, 358–375, 1937); (b) SF\(_6\) (data of M. W. Pestak et al, Phys. Rev. B, 36, 599–614, 1987, Table VII). Experimental gas densities are shown by open squares and experimental liquid densities by open triangles. The mean density at each experimental temperature is shown by an open circle. The open diamond is at the critical temperature and critical density.
The critical temperature of a substance can be measured quite accurately by observing the appearance or disappearance of a liquid–gas meniscus, and the critical pressure can be measured at this temperature with a high-pressure manometer. To evaluate the density at the critical point, it is best to extrapolate the mean density of the coexisting liquid and gas phases, \((\rho\sups{l} +\rho\sups{g})/2\), to the critical temperature as illustrated in Fig. 8.8. The observation that the mean density closely approximates a linear function of temperature, as shown in the figure, is known as the law of rectilinear diameters, or the law of Cailletet and Matthias. This law is an approximation, as can be seen by the small deviation of the mean density of SF\(_6\) from a linear relation very close to the critical point in Fig. 8.8(b). This failure of the law of rectilinear diameters is predicted by recent theoretical treatments (Jingtao Wang and Mikhail A. Anisimov, Phys. Rev. E, 75, 051107, 2007; Hassan Behnejad, Jan V. Sengers, and Mikhail A. Anisimov, in A. R. H. Goodwin, J. V. Sengers, and C. J. Peters, editors, Applied Thermodynamics of Fluids, pages 321–367, Royal Society of Chemistry, Cambridge, 2010).
8.2.4 The lever rule
Consider a single-substance system whose system point is in a two-phase area of a pressure–volume phase diagram. How can we determine the amounts in the two phases?
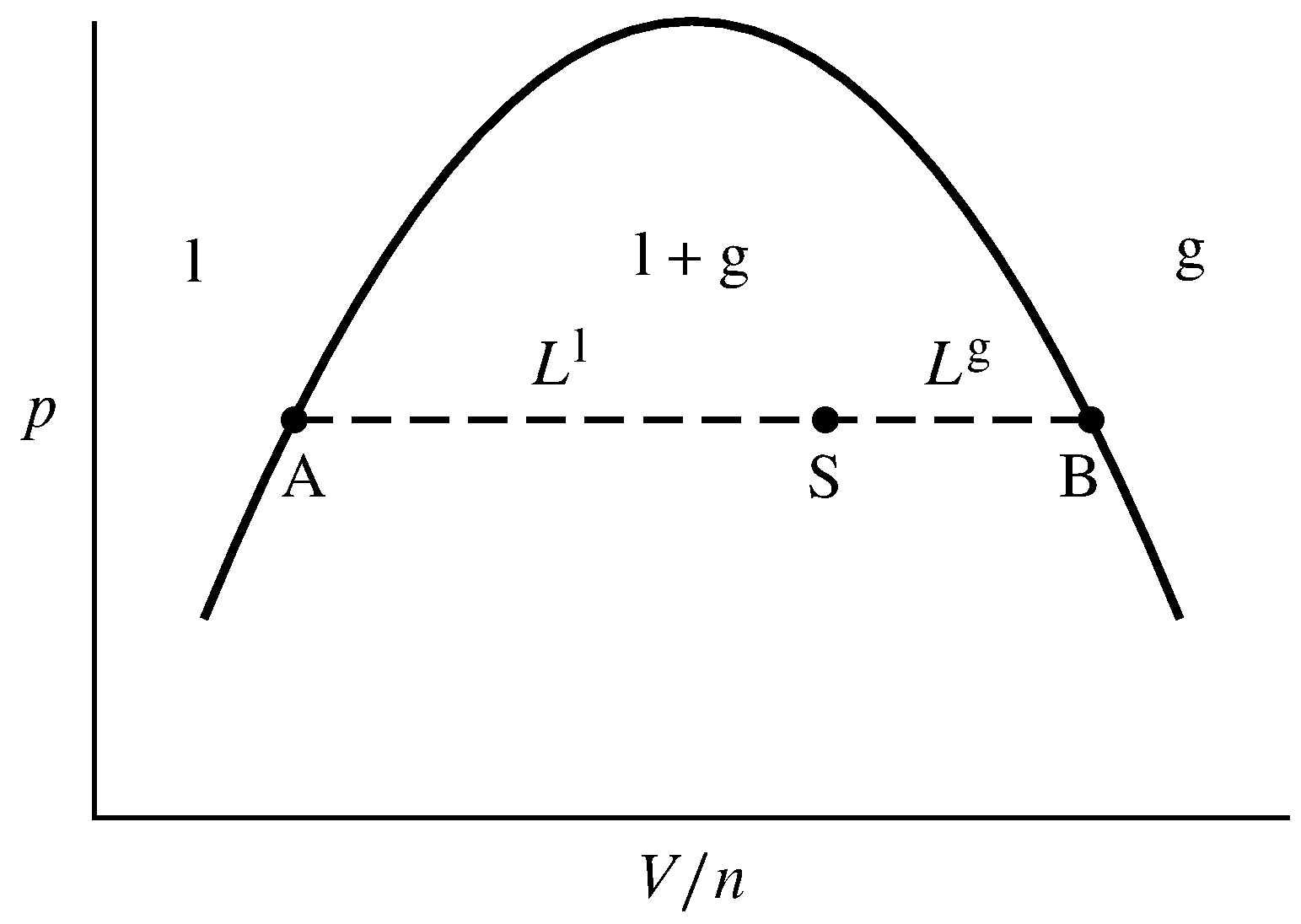
Figure 8.9 Tie line (dashed) at constant \(T\) and \(p\) in the liquid–gas area of a pressure–volume phase diagram. Points A and B are at the ends of the tie line, and point S is a system point on the tie line. \(L\sups{l}\) and \(L\sups{g}\) are the lengths AS and SB, respectively.
As an example, let the system contain a fixed amount \(n\) of a pure substance divided into liquid and gas phases, at a temperature and pressure at which these phases can coexist in equilibrium. When heat is transferred into the system at this \(T\) and \(p\), some of the liquid vaporizes by a liquid–gas phase transition and \(V\) increases; withdrawal of heat at this \(T\) and \(p\) causes gas to condense and \(V\) to decrease. The molar volumes and other intensive properties of the individual liquid and gas phases remain constant during these changes at constant \(T\) and \(p\). On the pressure–volume phase diagram of Fig. 8.9, the volume changes correspond to movement of the system point to the right or left along the tie line AB.
When enough heat is transferred into the system to vaporize all of the liquid at the given \(T\) and \(p\), the system point moves to point B at the right end of the tie line. \(V/n\) at this point must be the same as the molar volume of the gas, \(V\m\sups{g}\). We can see this because the system point could have moved from within the one-phase gas area to this position on the boundary without undergoing a phase transition.
When, on the other hand, enough heat is transferred out of the system to condense all of the gas, the system point moves to point A at the left end of the tie line. \(V/n\) at this point is the molar volume of the liquid, \(V\m\sups{l}\).
When the system point is at position S on the tie line, both liquid and gas are present. Their amounts must be such that the total volume is the sum of the volumes of the individual phases, and the total amount is the sum of the amounts in the two phases: \begin{equation} V = V\sups{l}+V\sups{g} = n\sups{l}V\m\sups{l}+n\sups{g}V\m\sups{g} \tag{8.2.1} \end{equation} \begin{equation} n = n\sups{l}+n\sups{g} \tag{8.2.2} \end{equation} The value of \(V/n\) at the system point is then given by the equation \begin{equation} \frac{V}{n} = \frac{n\sups{l}V\m\sups{l}+n\sups{g}V\m\sups{g}}{n\sups{l}+n\sups{g}} \tag{8.2.3} \end{equation} which can be rearranged to \begin{equation} n\sups{l}\left(V\m\sups{l}-\frac{V}{n}\right) =n\sups{g}\left(\frac{V}{n}-V\m\sups{g}\right) \tag{8.2.4} \end{equation} The quantities \(V\m\sups{l}-V/n\) and \(V/n-V\m\sups{g}\) are the lengths \(L\sups{l}\) and \(L\sups{g}\), respectively, defined in the figure and measured in units of \(V/n\). This gives us the lever rule for liquid–gas equilibrium: \begin{gather} \s{ n\sups{l} L\sups{l} = n\sups{g} L\sups{g} \quad \tx{or} \quad \frac{n\sups{g}}{n\sups{l} } = \frac{L\sups{l} }{L\sups{g}} } \tag{8.2.5} \cond{(coexisting liquid and gas} \nextcond{phases of a pure substance)} \end{gather} (The relation is called the lever rule by analogy to a stationary mechanical lever, each end of which has the same value of the product of applied force and distance from the fulcrum.)
In Fig. 8.9 the system point S is positioned on the tie line two thirds of the way from the left end, making length \(L\sups{l}\) twice as long as \(L\sups{g}\). The lever rule then gives the ratio of amounts: \(n\sups{g}/n\sups{l} = L\sups{l}/L\sups{g} =2\). One-third of the total amount is liquid and two-thirds is gas.
We cannot apply the lever rule to a point on the triple line, because we need more than the value of \(V/n\) to determine the relative amounts present in three phases.
We can derive a more general form of the lever rule that will be needed in Chap. 13 for phase diagrams of multicomponent systems. This general form can be applied to any two-phase area of a two-dimensional phase diagram in which a tie-line construction is valid, with the position of the system point along the tie line given by the variable \begin{equation} F \defn \frac{a}{b} \tag{8.2.6} \end{equation} where \(a\) and \(b\) are extensive state functions. (In the pressure–volume phase diagram of Fig. 8.9, these functions are \(a=V\) and \(b=n\) and the system point position is given by \(F=V/n\).) We repeat the steps of the derivation above, labeling the two phases by superscripts \(\pha\) and \(\phb\) instead of \(l\) and \(g\). The relation corresponding to Eq. 8.2.4 is \begin{equation} b\aph(F\aph-F)=b\bph(F-F\bph) \tag{8.2.7} \end{equation} If \(L\aph\) and \(L\bph\) are lengths measured along the tie line from the system point to the ends of the tie line at single phases \(\pha\) and \(\phb\), respectively, Eq. 8.2.7 is equivalent to the general lever rule \begin{equation} b\aph L\aph = b\bph L\bph \qquad \tx{or} \qquad \frac{b\bph}{b\aph} = \frac{L\aph}{L\bph} \tag{8.2.8} \end{equation}
8.2.5 Volume properties
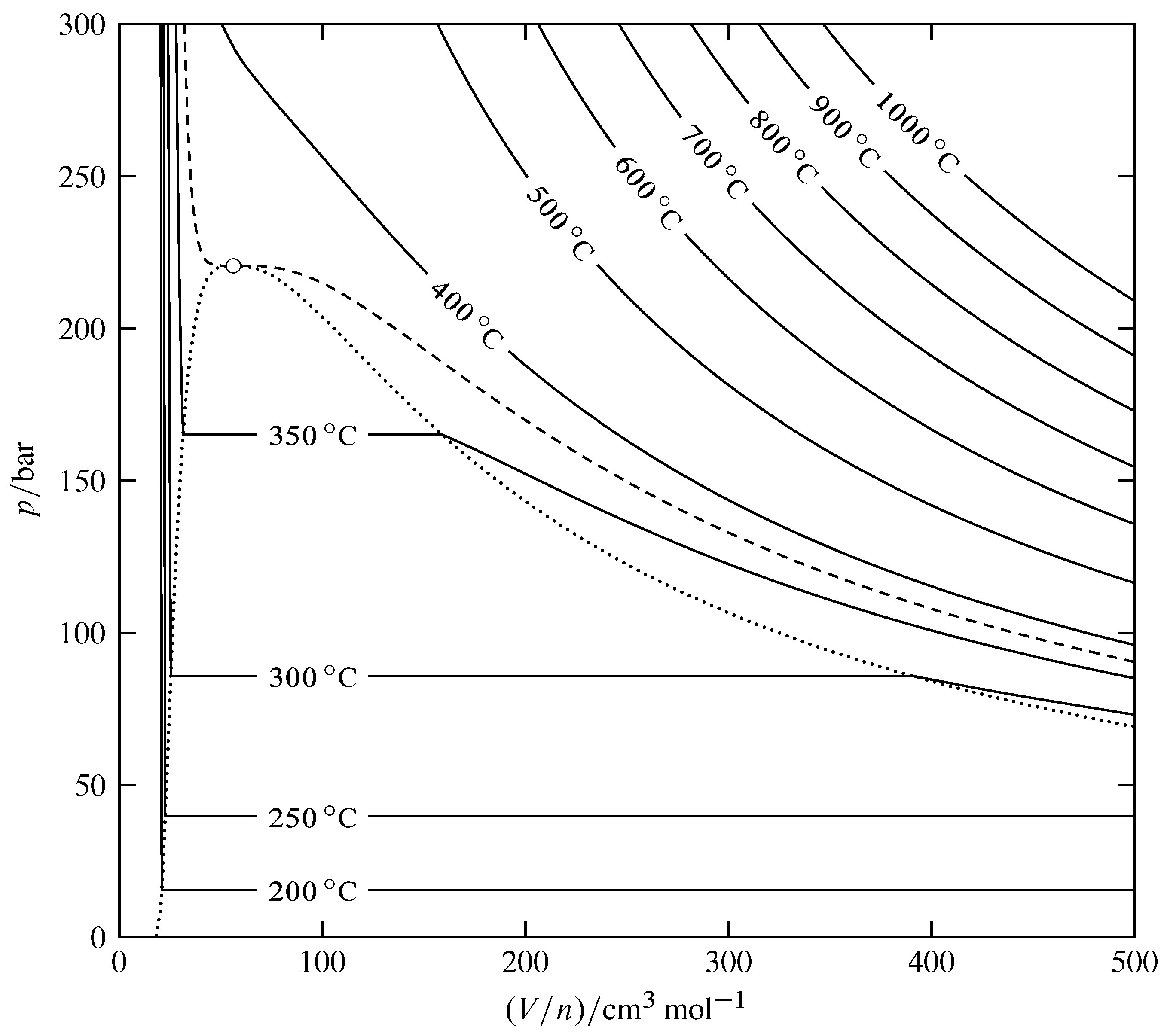
Figure 8.10 Isotherms for the fluid phases of H\(_2\)O (based on data in NIST Chemistry WebBook). The open circle indicates the critical point, the dashed curve is the critical isotherm at \(373.95\units{\(\degC\)}\), and the dotted curve encloses the two-phase area of the pressure–volume phase diagram. The triple line lies too close to the bottom of the diagram to be visible on this scale.
Figure 8.10 is a pressure–volume phase diagram for H\(_2\)O. On the diagram are drawn isotherms (curves of constant \(T\)). These isotherms define the shape of the three-dimensional \(p\)–\((V/n)\)–\(T\) surface. The area containing the horizontal isotherm segments is the two-phase area for coexisting liquid and gas phases. The boundary of this area is defined by the dotted curve drawn through the ends of the horizontal segments. The one-phase liquid area lies to the left of this curve, the one-phase gas area lies to the right, and the critical point lies at the top.
The diagram contains the information needed to evaluate the molar volume at any temperature and pressure in the one-phase region and the derivatives of the molar volume with respect to temperature and pressure. At a system point in the one-phase region, the slope of the isotherm passing through the point is the partial derivative \(\pd{p}{V\m}{T}\). Since the isothermal compressibility is given by \(\kT = -(1/V\m)\pd{V\m}{p}{T}\), we have \begin{equation} \kT = -\frac{1}{V\m \times \tx{slope of isotherm}} \tag{8.2.9} \end{equation} We see from Fig. 8.10 that the slopes of the isotherms are large and negative in the liquid region, smaller and negative in the gas and supercritical fluid regions, and approach zero at the critical point. Accordingly, the isothermal compressibility of the gas and the supercritical fluid is much greater than that of the liquid, approaching infinity at the critical point. The critical opalescence seen in Fig. 8.7 is caused by local density fluctuations, which are large when \(\kT\) is large.
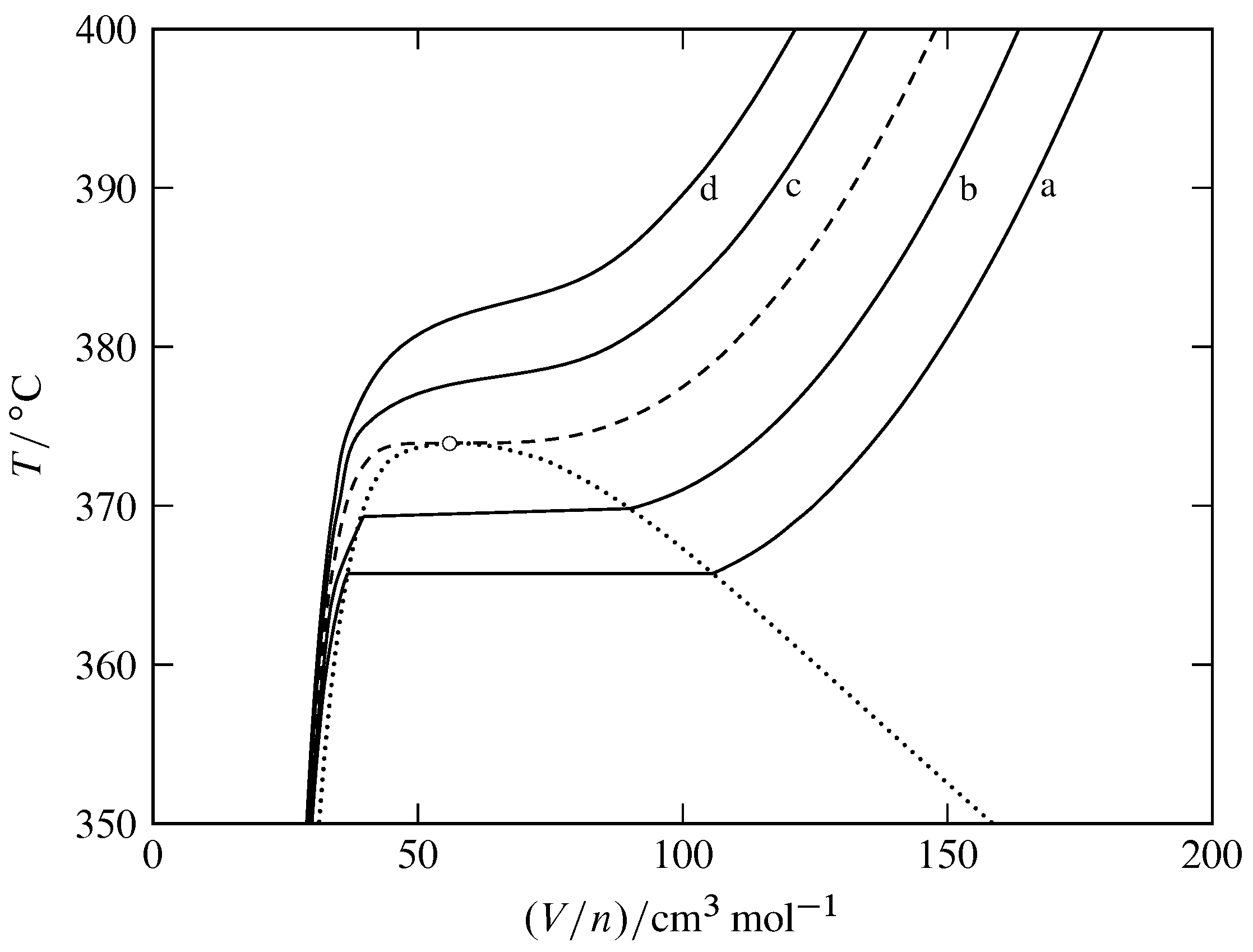
Figure 8.11 Isobars for the fluid phases of H\(_2\)O (based on data in NIST Chemistry WebBook). The open circle indicates the critical point, the dashed curve is the critical isobar at \(220.64\br\), and the dotted curve encloses the two-phase area of the temperature–volume phase diagram.
Solid curves: a, \(p=200\br\); b, \(p=210\br\); c, \(p=230\br\); d, \(p=240\br\).
Figure 8.11 shows isobars for H\(_2\)O instead of isotherms. At a system point in the one-phase region, the slope of the isobar passing through the point is the partial derivative \(\pd{T}{V\m}{p}\). The cubic expansion coefficient \(\alpha\) is equal to \((1/V\m)\pd{V\m}{T}{p}\), so we have \begin{equation} \alpha = \frac{1}{V\m \times \tx{slope of isobar}} \tag{8.2.10} \end{equation} The figure shows that the slopes of the isobars are large and positive in the liquid region, smaller and negative in the gas and supercritical fluid regions, and approach zero at the critical point. Thus the gas and the supercritical fluid have much larger cubic expansion coefficients than the liquid. The value of \(\alpha\) approaches infinity at the critical point, meaning that in the critical region the density distribution is greatly affected by temperature gradients. This may account for the low position of the middle ball in Fig. 8.7(b).


