3.11: Chapter 3 Problems
- Page ID
- 23705
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)An underlined problem number or problem-part letter indicates that the numerical answer appears in Appendix I.
3.1 Assume you have a metal spring that obeys Hooke's law: \(F=c\left(l-l_{0}\right)\), where \(F\) is the force exerted on the spring of length \(l, l_{0}\) is the length of the unstressed spring, and \(c\) is the spring constant. Find an expression for the work done on the spring when you reversibly compress it from length \(l_{0}\) to a shorter length \(l^{\prime}\).
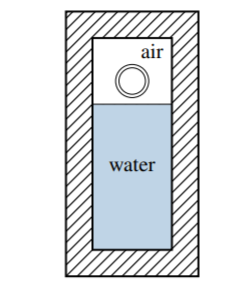
3.2 The apparatus shown in Fig. \(3.22\) consists of fixed amounts of water and air and an incompressible solid glass sphere (a marble), all enclosed in a rigid vessel resting on a lab bench. Assume the marble has an adiabatic outer layer so that its temperature cannot change, and that the walls of the vessel are also adiabatic.
Initially the marble is suspended above the water. When released, it falls through the air into the water and comes to rest at the bottom of the vessel, causing the water and air (but not the marble) to become slightly warmer. The process is complete when the system returns to an equilibrium state. The system energy change during this process depends on the frame of reference and on how the system is defined. \(\Delta E_{\text {sys }}\) is the energy change in a lab frame, and \(\Delta U\) is the energy change in a specified local frame.
For each of the following definitions of the system, give the sign (positive, negative, or zero) of both \(\Delta E_{\text {sys }}\) and \(\Delta U\), and state your reasoning. Take the local frame for each system to be a center-of-mass frame.
(a) The system is the marble.
(b) The system is the combination of water and air.
(c) The system is the combination of water, air, and marble.
3.3 Figure \(3.23\) shows the initial state of an apparatus consisting of an ideal gas in a bulb, a stopcock, a porous plug, and a cylinder containing a frictionless piston. The walls are diathermal, and the surroundings are at a constant temperature of \(300.0 \mathrm{~K}\) and a constant pressure of \(1.00 \mathrm{bar}\).
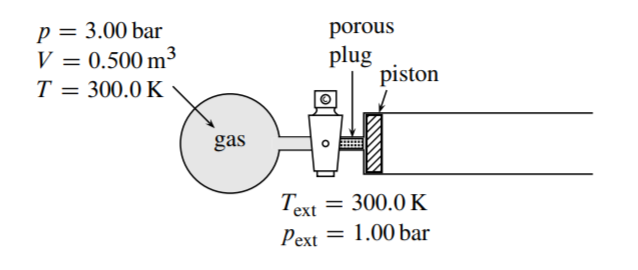
When the stopcock is opened, the gas diffuses slowly through the porous plug, and the piston moves slowly to the right. The process ends when the pressures are equalized and the piston stops moving. The system is the gas. Assume that during the process the temperature throughout the system differs only infinitesimally from \(300.0 \mathrm{~K}\) and the pressure on both sides of the piston differs only infinitesimally from \(1.00\) bar.
(a) Which of these terms correctly describes the process: isothermal, isobaric, isochoric, reversible, irreversible?
(b) Calculate \(q\) and \(w\).
3.4 Consider a horizontal cylinder-and-piston device similar to the one shown in Fig. \(3.5\) on page 72. The piston has mass \(m\). The cylinder wall is diathermal and is in thermal contact with a heat reservoir of temperature \(T_{\text {ext }}\). The system is an amount \(n\) of an ideal gas confined in the cylinder by the piston.
The initial state of the system is an equilibrium state described by \(p_{1}\) and \(T=T_{\text {ext }}\). There is a constant external pressure \(p_{\text {ext }}\), equal to twice \(p_{1}\), that supplies a constant external force on the piston. When the piston is released, it begins to move to the left to compress the gas. Make the idealized assumptions that (1) the piston moves with negligible friction; and (2) the gas remains practically uniform (because the piston is massive and its motion is slow) and has a practically constant temperature \(T=T_{\text {ext }}\) (because temperature equilibration is rapid).
(a) Describe the resulting process.
(b) Describe how you could calculate \(w\) and \(q\) during the period needed for the piston velocity to become zero again.
(c) Calculate \(w\) and \(q\) during this period for \(0.500 \mathrm{~mol}\) gas at \(300 \mathrm{~K}\).
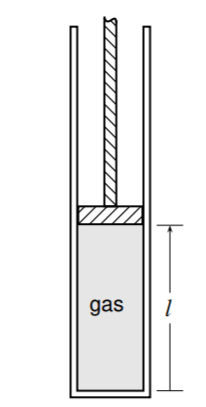
3.5 This problem is designed to test the assertion on page 60 that for typical thermodynamic processes in which the elevation of the center of mass changes, it is usually a good approximation to set \(w\) equal to \(w_{\text {lab. }}\). The cylinder shown in Fig. \(3.24\) on the preceding page has a vertical orientation, so the elevation of the center of mass of the gas confined by the piston changes as the piston slides up or down. The system is the gas. Assume the gas is nitrogen \(\left(M=28.0 \mathrm{~g} \mathrm{~mol}^{1}\right)\) at \(300 \mathrm{~K}\), and initially the vertical length \(l\) of the gas column is one meter. Treat the nitrogen as an ideal gas, use a center-of-mass local frame, and take the center of mass to be at the midpoint of the gas column. Find the difference between the values of \(w\) and \(w_{\text {lab }}\), expressed as a percentage of \(w\), when the gas is expanded reversibly and isothermally to twice its initial volume.
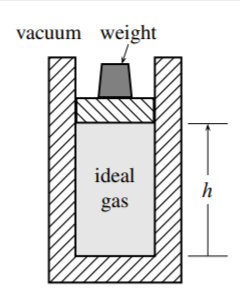
3.6 Figure \(3.25\) shows an ideal gas confined by a frictionless piston in a vertical cylinder. The system is the gas, and the boundary is adiabatic. The downward force on the piston can be varied by changing the weight on top of it.
(a) Show that when the system is in an equilibrium state, the gas pressure is given by \(p=\) \(m g h / V\) where \(m\) is the combined mass of the piston and weight, \(g\) is the acceleration of free fall, and \(h\) is the elevation of the piston shown in the figure.
(b) Initially the combined mass of the piston and weight is \(m_{1}\), the piston is at height \(h_{1}\), and the system is in an equilibrium state with conditions \(p_{1}\) and \(V_{1}\). The initial temperature is \(T_{1}=p_{1} V_{1} / n R\). Suppose that an additional weight is suddenly placed on the piston, so that \(m\) increases from \(m_{1}\) to \(m_{2}\), causing the piston to sink and the gas to be compressed adiabatically and spontaneously. Pressure gradients in the gas, a form of friction, eventually cause the piston to come to rest at a final position \(h_{2}\). Find the final volume, \(V_{2}\), as a function of \(p_{1}, p_{2}, V_{1}\), and \(C_{V} .\) (Assume that the heat capacity of the gas, \(C_{V}\), is independent of temperature.) Hint: The potential energy of the surroundings changes by \(m_{2} g \Delta h\); since the kinetic energy of the piston and weights is zero at the beginning and end of the process, and the boundary is adiabatic, the internal energy of the gas must change by \(-m_{2} g \Delta h=-m_{2} g \Delta V / A_{\mathrm{s}}=-p_{2} \Delta V\).
(c) It might seem that by making the weight placed on the piston sufficiently large, \(V_{2}\) could be made as close to zero as desired. Actually, however, this is not the case. Find expressions for \(V_{2}\) and \(T_{2}\) in the limit as \(m_{2}\) approaches infinity, and evaluate \(V_{2} / V_{1}\) in this limit if the heat capacity is \(C_{V}=(3 / 2) n R\) (the value for an ideal monatomic gas at room temperature).
3.7 The solid curve in Fig. \(3.7\) shows the path of a reversible adiabatic expansion or compression of a fixed amount of an ideal gas. Information about the gas is given in the figure caption. For compression along this path, starting at \(V=0.3000 \mathrm{dm}^{3}\) and \(T=300.0 \mathrm{~K}\) and ending at \(V=0.1000 \mathrm{dm}^{3}\), find the final temperature to \(0.1 \mathrm{~K}\) and the work.
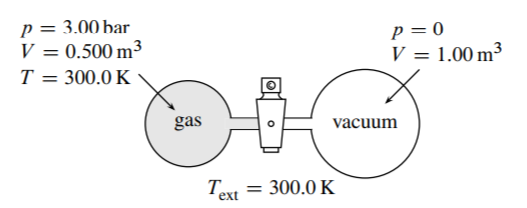
3.8 Figure \(3.26\) shows the initial state of an apparatus containing an ideal gas. When the stopcock is opened, gas passes into the evacuated vessel. The system is the gas. Find \(q, w\), and \(\Delta U\) under the following conditions.
(a) The vessels have adiabatic walls.
(b) The vessels have diathermal walls in thermal contact with a water bath maintained at \(300 . \mathrm{K}\), and the final temperature in both vessels is \(T=300 . \mathrm{K}\).
3.9 Consider a reversible process in which the shaft of system A in Fig. \(3.11\) makes one revolution in the direction of increasing \(\vartheta\). Show that the gravitational work of the weight is the same as the shaft work given by \(w=m g r \Delta \vartheta\).
Table 3.2 Data for Problem 3.10. The values are from Joule's 1850 paper \(^{a}\) and have been converted to SI units.
\({ }^{a}\) Ref. [91], p. 67, experiment \(5 .\)
\({ }^{b}\) Calculated from the masses and specific heat capacities of the materials.
3.10 This problem guides you through a calculation of the mechanical equivalent of heat using data from one of James Joule's experiments with a paddle wheel apparatus (see Sec. 3.7.2). The experimental data are collected in Table 3.2.
In each of his experiments, Joule allowed the weights of the apparatus to sink to the floor twenty times from a height of about \(1.6 \mathrm{~m}\), using a crank to raise the weights before each descent (see Fig. \(3.14\) on page 89). The paddle wheel was engaged to the weights through the roller and strings only while the weights descended. Each descent took about 26 seconds, and the entire experiment lasted 35 minutes. Joule measured the water temperature with a sensitive mercury-in-glass thermometer at both the start and finish of the experiment.
For the purposes of the calculations, define the system to be the combination of the vessel, its contents (including the paddle wheel and water), and its lid. All energies are measured in a lab frame. Ignore the small quantity of expansion work occurring in the experiment. It helps conceptually to think of the cellar room in which Joule set up his apparatus as being effectively isolated from the rest of the universe; then the only surroundings you need to consider for the calculations are the part of the room outside the system.
(a) Calculate the change of the gravitational potential energy \(E_{\mathrm{p}}\) of the lead weights during each of the descents. For the acceleration of free fall at Manchester, England (where Joule carried out the experiment) use the value \(g=9.813 \mathrm{~m} \mathrm{~s}^{-2}\). This energy change represents a decrease in the energy of the surroundings, and would be equal in magnitude and opposite in sign to the stirring work done on the system if there were no other changes in the surroundings.
(b) Calculate the kinetic energy \(E_{\mathrm{k}}\) of the descending weights just before they reached the floor. This represents an increase in the energy of the surroundings. (This energy was dissipated into thermal energy in the surroundings when the weights came to rest on the floor.)
(c) Joule found that during each descent of the weights, friction in the strings and pulleys decreased the quantity of work performed on the system by \(2.87 \mathrm{~J}\). This quantity represents an increase in the thermal energy of the surroundings. Joule also considered the slight stretching of the strings while the weights were suspended from them: when the weights came to rest on the floor, the tension was relieved and the potential energy of the strings changed by \(-1.15 \mathrm{~J}\). Find the total change in the energy of the surroundings during the entire experiment from all the effects described to this point. Keep in mind that the weights descended 20 times during the experiment.
(d) Data in Table \(3.2\) show that change of the temperature of the system during the experiment was
\[
\Delta T=(289.148-288.829) \mathrm{K}=+0.319 \mathrm{~K}
\]
The paddle wheel vessel had no thermal insulation, and the air temperature was slighter warmer, so during the experiment there was a transfer of some heat into the system. From a correction procedure described by Joule, the temperature change that would have occurred if the vessel had been insulated is estimated to be \(+0.317 \mathrm{~K}\).
Use this information together with your results from part (c) to evaluate the work needed to increase the temperature of one gram of water by one kelvin. This is the "mechanical equivalent of heat" at the average temperature of the system during the experiment. (As mentioned on p. 87 , Joule obtained the value \(4.165 \mathrm{~J}\) based on all 40 of his experiments.)
3.11 Refer to the apparatus depicted in Fig. \(3.1\) on page 61. Suppose the mass of the external weight is \(m=1.50 \mathrm{~kg}\), the resistance of the electrical resistor is \(R_{\mathrm{el}}=5.50 \mathrm{k} \Omega\), and the acceleration of free fall is \(g=9.81 \mathrm{~m} \mathrm{~s}^{-2}\). For how long a period of time will the external cell need to operate, providing an electric potential difference \(|\Delta \phi|=1.30 \mathrm{~V}\), to cause the same change in the state of the system as the change when the weight sinks \(20.0 \mathrm{~cm}\) without electrical work? Assume both processes occur adiabatically.


