4.5: Combinatorics and Multiplicity
- Page ID
- 236434
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Definitions
Combinatorics: a branch of mathematics that deals with the rules for combining different outcomes and events and calculating the probabilities of these combinations.
Probability: The probability of an outcome is a measure of the likelihood that the outcome will occur in comparison to all possible outcomes.
Permutation: one “way” in which all or part of a set of objects can be ordered or arranged.
Combination: one “way” of selecting all or part of a set of objects without regard to the order in which the objects are selected.
Multiplicity: the multiplicity of events is the total number of “ways” in which different outcomes can possibly occur. Represented by the symbol W, and also called ways, permutations, sequences, degeneracy, weight, arrangements, thermodynamic probability, etc. depending on the context.
As you can see from these definitions, combinatorics is the branch of math related to counting events and outcomes, while multiplicity is the statistical thermodynamics variable equal to the number of possible outcomes. They are intricately connected.
Depending on the situation, this number of possible outcomes (multiplicity) could be calculated using the fundamental principles of counting, permutation formulas, or combination formulas from the field of combinatorics. Below is a detailed explanation and example of each of these counting methods and when they can be applied.
The Fundamental Principles of Counting
The Multiplication Principle
During restaurant week, you go out to eat for dinner. The restaurant week menu gives you the option to choose between three appetizers, four entrées, and two desserts. You feel a bit overwhelmed by the number of possibilities; how many different meal options are there?
- Each of these selection events has a different number of possible outcomes or options:
- Appetizer selection = 3 options
- Entrée selection = 4 options
- Dessert event = 2 options
- Because you will choose one appetizer AND one entrée AND one dessert, the total number of different ways your meal could be prepared is: \[W=3 \times 4 \times 2=24\]
- One of the Fundamental Principles of Counting, the Multiplication Principle states that if there are n possible outcomes for each event type, i, in a sequence, then the total number of possible outcomes is equal to the values of n multiplied together: \[W=n_{1} n_{2} \cdots n_{t}=\prod_{i=1}^{t} n_{i}\] where \(\prod\) symbol is the product operator (similar to \(\sum\) symbol for the sum operator).
- In this context, each \(n_i\) represents the number of possible outcomes for each event. Therefore, the multiplicity of each event type, \(W_i\), is equal to \(n_i\), and the total multiplicity, \(W_{t o t a l}\), can be determined by: \[W_{t o t a l}=W_{1} W_{2} \cdots W_{3}=\prod_{i=1}^{t} W_{i}\]
The Addition Principle
You are looking to buy a new binder to store your class notes. You’re torn between a 1” binder and a 1.5” binder. The 1” binder comes in 5 colors and the 1.5” binder comes in 3. How many total binder options are you considering?
- The two binders each has a different number of possible outcomes:
- 1” binder = 5 outcomes
- 1.5” binder = 3 outcomes
- Because you will choose a 1” binder OR a 1.5” binder, the total number of different outcomes you are considering is: \[W=5+3=8\]
- One of the Fundamental Principles of Counting, the Addition Principle states that if there are n possible outcomes for each event, i, and we cannot do both at the same time, then the total number of possible outcomes is equal to the values of n added together: \[W=n_{1}+n_{2}+n_{3} \cdots=\sum_{i=1}^{t} n_{i}\]
Permutations
Permutations of distinguishable outcomes without repetition: ALL outcomes selected
You decide to take on the challenge of trying each of CookOut’s 40 flavors of milkshakes! If you have a different milkshake each day until you’ve tried them all (no repeats!), how many different sequences of milkshakes (i.e., orders or arrangements) are possible?
- Since you are not repeating any milkshakes during this time, you will choose from 40 milkshakes on day one AND 39 on day two AND 38 on day three, etc. According to the Multiplication Principle above, the total number of sequences is: \[W=40 \times 39 \times 38 \times 37 \times \cdots \times 2 \times 1=40 !=8.16 \times 10^{47}\]
- The order of the milkshakes matters in this question but no milkshakes are repeated; this is called a permutation without repetition: \[W=N !\] where \(N\) is the total number of possible outcomes and all possible outcomes are sampled (i.e., you will keep selecting milkshakes until you’ve tried all the milkshakes). Because you can identify which milkshake you are trying each day, the outcomes or options are considered distinguishable.
Permutations of distinguishable outcomes without repetition: SOME outcomes only
On second thought, having a different milkshake every day for 40 days may be a bit much… Instead, you decide to have a different milkshake every day for a week. (Then you’ll take a break and come back to tackle the rest of the menu in the future!) How many different arrangements or sequences are possible during the first week?
- The math is similar to the previous question, except that we only need to multiply the first seven of the numbers in the factorial for the first seven days: \[W=40 \times 39 \times 38 \times 37 \times 36 \times 35 \times 34=93963542400\]
- A more general expression for this permutation without repetition includes the total number of possible outcomes, N, and the total number of selection events, r, which is expressed as “\(N\), take \(r\)” (or you may want to think of it as “\(N\), arrange \(r\)”): \[W=\ _{N}P_{r}=\frac{N !}{(N-r) !}\] where \( _{N}P_{r}\) is a common notation for permutation without repetition.
- For our example, this would be: \[W={ }_{40} P_{7}=\frac{40 !}{(40-7) !}=\frac{40 !}{33 !}=\frac{40 \times 39 \times 38 \times 37 \times 36 \times 35 \times 34 \times 33 !}{33 !}=93963542400\]
- The previous example (with all 40 milkshakes) can also be depicted this way, however, since all items are selected, \(N\) and \(r\) are equal: \[W={ }_{40} P_{40}=\frac{40 !}{(40-40) !}=\frac{40 !}{0 !}=40!\]
Permutations of distinguishable outcomes with repetition
To help power you through finals, you decide to have a milkshake every day during finals week, but you are not going to bother with trying different ones; you may just decide to have the same one every day! What would the total number of milkshake sequences be in this case?
- If every day you have the option of 40 different milkshakes, the number of possible sequences is: \[W=40 \times 40 \times 40 \times 40 \times 40 \times 40 \times 40=40^{7}=163840000000\]
- This is a permutation with repetition, and the equation gives the number of possible sequences for r events that each have N possible outcomes: \[W=N^{r}\]
- The term repetition indicates that an outcome or object is not removed from the available pool after selection. Another way to refer to this concept is as permutation with replacement; after selecting a particular outcome, that outcome is returned to the selection pool so that the available selection options are always the same.
Permutations of indistinguishable outcomes
Over winter break, you purchase an 11 oz bag of Holiday Milk Chocolate Hershey’s Kisses. In the bag of 72 kisses, you have 25 red, 23 silver, and 24 green kisses. If you pull the kisses out of the bag one at a time, how many different sequences of holiday colors are possible?
- It may seem that this description also refers to calculating the number of permutations for items that repeat (since there are multiple kisses of each wrapper color), and in fact, some resources do refer to the equation that way. However, this scenario does not repeat in the same way as the previous example.
- The term repetition is used for a series of events or set of objects where the outcomes are allowed to repeat after being selected (i.e., the selection pool does not change because the selected outcome is replaced by another outcome of the same type).
- In the current scenario, the selected individual kisses do not “repeat” because they are not returned to the bag; as each kiss is removed, the available selection pool decreases. Instead, there are simply multiple indistinguishable items in the selection pool before the selections begin. This makes a difference in terms of how many items of each type (i.e., kisses of each color) are available to be selected.
- If our kisses were labeled so that each kiss was distinguishable from the others, then our total number of permutations would be calculated as described previously: \[W=72 !\] However, this calculation will count \(red_A\) followed by \(red_B\) as a different sequence from \(red_B\) followed by \(red_A\). These two outcomes are indistinguishable without the A and B labels, so the number of unique sequences must be determined by factoring out the number of identical or redundant arrangements.
- The number of possible arrangements for each individual type of kiss is: \[n_{r e d} =25 !\] \[n_{s i l v e r} =23 ! \] \[n_{g r e e n} =24 !\] Therefore, our number of unique sequences or arrangements is: \[W=\frac{N !}{n_{red} ! n_{silver} ! n_{green} !}=\frac{72 !}{25 ! 23 ! 24 !}\]
- Another way to refer to this type of permutation is a multiset permutation because the overall set is composed of smaller subsets of indistinguishable outcomes. The general expression for a multiset permutation is: \[W=\frac{N !}{n_{1} ! n_{2} ! \cdots n_{t} !}\] where each \(n_i\) is the number of possible outcomes for each selection type, \(i\), and the total number of outcomes or objects, \(N\), is: \[N=\sum_{i=1}^{t} n_{i}\]
Combinations
Combinations without repetition
In the spring semester, you decide you’ve had enough CookOut milkshakes for a while. You buy Blue Bell ice cream from the grocery store instead! You stock 5 flavors: cookies and cream (CC), mint chocolate chip (M), strawberry (S), Dutch chocolate (DC), and banana pudding (B). If you always get three scoops of different flavors, how many different combinations are possible?
- Let’s list our five available flavors of ice cream:

Assume we choose B for the first scoop. If we cannot have each flavor more than once (i.e., without repetition), then B is no longer an option for the remaining scoops. Therefore, the second scoop only has four choices available to it:

We choose S for the second scoop, and remove it from the available flavors:

Lastly, we choose DC for the third scoop:

- Thus far, this process looks like a permutation without repeats, and the permutation equation would yield: \[{ }_{5} P_{3}=\frac{5 !}{(5-3) !}=\frac{5 !}{2 !}=5 \times 4 \times 3=60\]
However, the combination {B, S, DC} is indistinguishable from other combinations of B, S, and DC scooped in a different order. Once in the bowl, order does not matter. The permutation equation would count each sequence of B, S, and DC separately, so we need to correct for the number of duplicate or indistinguishable combinations.
We can illustrate this point further by looking at the example of B, S, and DC in more details:

There are six distinguishable sequences that produce indistinguishable combinations. We could also calculate this value using the permutation without repetition for the number of scoops: \[\ _{3} P_{3}=\frac{3 !}{(3-3) !}=\frac{3 !}{0 !}=3 !=6\]
- To determine the number of unique or distinguishable combinations (where order does not matter), we need to divide our number of distinguishable sequences by the number of sequences that produce indistinguishable combinations: \[W=\frac{60}{6}=10\] \[W=\frac{ _{5} P_{3}}{3 !}=\frac{\frac{5 !}{(5-3) !}}{3 !}=\frac{5 !}{(5-3) ! 3 !}=\frac{5 !}{2 ! 3 !}=10\]
- The general equation for this combination without repetition, which is referred to as “\(N\), choose \(r\)” (or in our case “5 ice cream flavors, choose 3”) is:
\[W=\ _{N} C_{r}=\left(\begin{array}{l}
N \\
r
\end{array}\right)=\frac{ _{N} P_{r}}{r !}=\frac{N !}{(N-r) ! r !}\]
where \(\ _{N} C_{r}\) and \(\left(\begin{array}{l}
N \\
r
\end{array}\right)\) are common notations for combination without repetition.
Combinations with repetition
Instead of always doing three different scoops, how many different combinations are possible if you do include repetitions (i.e. combinations with more than one scoop of a particular flavor)?
- This concept is called combination with repetition or combination with replacement. In this case, it’s easier to think about as replacement.
Let’s list our five flavors of ice cream again:

Assume we choose B for the first scoop. However, unlike before, after B has been taken from the available flavors, we will replace it with another B, leaving the selection options the same:

We choose a second scoop of B next, replacing it again with another B:

Lastly, we choose DC for the last scoop:

- What you can see is that, if you have repetition or replacements, you do not end up with “5, choose 3.” Instead, because of the replacements after the first two scoops, you had 7 total available choices during the selection process, making “7, choose 3.” \[W=\ _{7} C_{3}=\frac{7 !}{4 ! 3 !}=35\]
- In considering this more generally, hopefully you can recognize that, regardless of whatever number of \(N_initial\) options you started with, if you allow replacements, you will end up adding \((r-1)\) additional options (one fewer then the number of selections) by your final choice. Your final number of available options, therefore, becomes: \[N_{\text {final}}=N_{\text {initial}}+(r-1)\] We can take this expression for the final number of available choices and substitute it into the combination formula from the previous example: \[\ _{N} C_{r}=\frac{N !}{(N-r) ! r !}=\frac{N_{\text {final}} !}{\left(N_{\text {final}}-r\right) ! r !}=\frac{\left(N_{\text {initial}}+(r-1)\right) !}{\left(N_{\text {initial}}+(r-1)-r\right) ! r !}=\frac{\left(N_{\text {initial}}+(r-1)\right) !}{\left(N_{\text {initial}}-1\right) ! r !}\]We can rearrange this equation as: \[\left(\left(\begin{array}{l}
N \\
r
\end{array}\right)\right)=\frac{\left(\left(N_{\text {initial}}-1\right)+r\right) !}{\left(N_{\text {initial}}-1\right) ! r !}\] where the notation \(\left(\left(\begin{array}{l}
N \\
r
\end{array}\right)\right)\) is used to denote a combination with replacement and is called “\(N\), multichoose \(r\).” - This new expression resembles a permutation for two items with indistinguishable outcomes: there are \((N_{\text {initial}}-1)\) indistinguishable outcomes of one item and \(r\) of the other. This is from where the line/dot representation comes.
We will develop the system as having \((N_{\text {initial}}-1 )\) lines and \(r\) dots. Therefore, for our 5 ice cream flavors and 3 scoops, we will use 4 lines and 3 dots: \[W=\frac{(4+3) !}{4 ! 3 !}=35\]
- While this equation gives the correct answer, it may still seem strange to recast the problem in this way. Let’s look at it one more time: pretend you had an ice cream scooping machine, and you gave this machine instructions in a code of lines and dots. Each dot represents one scoop of ice cream, and each line separates (or partitions) one flavor from another. In order to communicate the combination of {B, B, DC} to the machine, you send the following code (remembering that order does not matter):
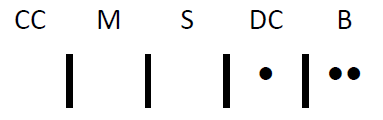
If you wanted {CC, M, DC}, it would be:
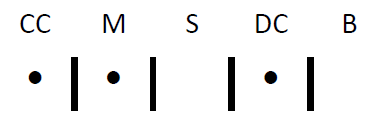
And if you wanted all CC:
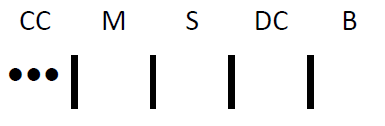
To demonstrate that the line/dot method works generally, recognize that, for \(N_{\text {initial}}\) options, there will always be \((N_{\text {initial}}-1 )\) lines needed to separate them from one another. For \(r\) choices, you will always need a total of \(r\) dots, one for each choice. It works to use three dots placed among four lines that separate the five flavors!
Therefore, the “\(N\), multichoose \(r\)” combination with replacement equation is equal to the permutation equation for \((N_{\text {initial}}-1 )\) lines and \(r\) dots, where the lines and dots are indistinguishable: \[\left(\left(\begin{array}{l}
N \\
r
\end{array}\right)\right)={ }_{N-1} P_{r}=\frac{((N-1)+r) !}{(N-1) ! r !}\]


