2.1: Kinetic Molecular Theory
- Page ID
- 236426
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- To understand the significance of the kinetic molecular theory of gases.
The laws that describe the behavior of gases were well established long before anyone had developed a coherent model of the properties of gases. In this section, we introduce a theory that describes why gases behave the way they do. The theory we introduce can also be used to derive laws such as the ideal gas law from fundamental principles and the properties of individual particles.
A Molecular Description
The kinetic molecular theory of gases explains the laws that describe the behavior of gases. Developed during the mid-19th century by several physicists, including the Austrian Ludwig Boltzmann (1844–1906), the German Rudolf Clausius (1822–1888), and the Englishman James Clerk Maxwell (1831–1879), who is also known for his contributions to electricity and magnetism, this theory is based on the properties of individual particles as defined for an ideal gas and the fundamental concepts of physics. Thus the kinetic molecular theory of gases provides a molecular explanation for observations that led to the development of the ideal gas law. The kinetic molecular theory of gases is based on the following four postulates:
four postulates of Kinetic Molecular Theory
- A gas is composed of a large number of particles called molecules (whether monatomic or polyatomic) that move randomly in straight-line, continuous motion.
- Gas molecules collide with one another and with the walls of the container, but these collisions are perfectly elastic; that is, they do not change the average kinetic energy of the molecules.
- Because the distance between gas molecules is much greater than the size of the molecules, the volume of the molecules is negligible. They are considered "point" particles.
- Intermolecular interactions, whether repulsive or attractive, are so weak that they are also negligible.
Although the molecules of real gases have nonzero volumes and exert both attractive and repulsive forces on one another, for the moment we will focus on how the kinetic molecular theory of gases relates to the properties of gases we have been discussing. In the following sections, we explain how this theory must be modified to account for the behavior of real gases.

Postulates 1 and 2 state that gas molecules are in constant motion and collide frequently with the walls of their containers. The collision of molecules with their container walls results in a momentum transfer (impulse) from molecules to the walls (Figure \(\PageIndex{2}\)).
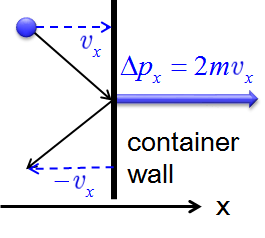
The momentum transfer to the wall perpendicular to \(x\) axis as a molecule with an initial velocity \(v_x\) in \(x\) direction hits is expressed as:
\[\Delta p_x=2mv_x \label{10.7.1}\]
The collision frequency, a number of collisions of the molecules to the wall per unit area and per second, increases with the molecular speed and the number of molecules per unit volume.
\[f\propto (v_x) \times \Big(\dfrac{N}{V}\Big) \label{10.7.2}\]
The pressure the gas exerts on the wall is expressed as the product of impulse and the collision frequency.
\[P\propto (2mv_x)\times(v_x)\times\Big(\dfrac{N}{V}\Big)\propto \Big(\dfrac{N}{V}\Big)mv_x^2 \label{10.7.3}\]
At any instant, however, the molecules in a gas sample are traveling at different speed. Therefore, we must replace \(v_x^2\) in the expression above with the average value of \(v_x^2\), which is denoted by \(\left\langle v_x^{2}\right\rangle\). The overbar designates the average value over all molecules.
The exact expression for pressure is given as :
\[P=\dfrac{N}{V}m\left\langle v_x^{2}\right\rangle\label{10.7.4}\]
Finally, we must consider that there is nothing special about \(x\) direction. We should expect that
\[\left\langle v_x^{2}\right\rangle= \left\langle v_y^{2}\right\rangle=\left\langle v_z^{2}\right\rangle=\dfrac{1}{3}\left\langle v^{2}\right\rangle\]
Here the quantity \(\left\langle v^{2}\right\rangle\) is called the mean-square speed defined as the average value of square-speed (\(v^2\)) over all molecules. Since
\[v^2=v_x^2+v_y^2+v_z^2\]
for each molecule, then
\[\left\langle v^{2}\right\rangle=\left\langle v_x^{2}\right\rangle+\left\langle v_y^{2}\right\rangle+\left\langle v_z^{2}\right\rangle\]
By substituting \(\dfrac{1}{3}\left\langle v^{2}\right\rangle\) for \(\left\langle v_x^{2}\right\rangle\) in the expression above, we can get the final expression for the pressure:
\[P=\dfrac{1}{3}\dfrac{N}{V}m\left\langle v^{2}\right\rangle \label{10.7.5}\]
Because volumes and intermolecular interactions are negligible, postulates 3 and 4 state that all gaseous particles behave identically, regardless of the chemical nature of their component molecules. This is the essence of the ideal gas law, which treats all gases as collections of particles that are identical in all respects except mass. Postulate 3 also explains why it is relatively easy to compress a gas; you simply decrease the distance between the gas molecules.
Additionally, the average kinetic energy of the molecules of any gas depends on only the temperature, and at a given temperature, all gaseous molecules have exactly the same average kinetic energy. This is sometimes considered Postulate 5 of Kinetic Molecular Theory. This postulate provides a molecular explanation for the temperature of a gas. It refers to the average translational kinetic energy of the molecules of a gas \(\left\langle {E_k}\right\rangle\), which can be represented as and states that at a given Kelvin temperature \((T)\), all gases have the same value of
\[\left\langle {E_k}\right\rangle=\dfrac{1}{2}m\left\langle v^{2}\right\rangle=\dfrac{3}{2}\dfrac{R}{N_A}T \label{10.7.6}\]
where \(N_A\) is the Avogadro's constant. The total translational kinetic energy of 1 mole of molecules can be obtained by multiplying the equation by \(N_A\):
\[N_A\left\langle {E_k}\right\rangle=\dfrac{1}{2}M\left\langle v^{2}\right\rangle=\dfrac{3}{2}RT \label{10.7.7}\]
where \(M\) is the molar mass of the gas molecules and is related to the molecular mass by \(M=N_Am\). By rearranging the equation, we can get the relationship between the root-mean square speed (\(v_{\rm rms}\)) and the temperature. The rms speed (\(v_{\rm rms}\)) is the square root of the sum of the squared speeds divided by the number of particles:
\[v_{\rm rms}=\sqrt{ \left\langle v^{2}\right\rangle }=\sqrt{\dfrac{v_1^2+v_2^2+\cdots v_N^2}{N}} \label{10.7.8}\]
where \(N\) is the number of particles and \(v_i\) is the speed of particle \(i\).
The relationship between \(v_{\rm rms}\) and the temperature is given by:
\[v_{\rm rms}=\sqrt{\dfrac{3RT}{M}} \label{10.7.9}\]
In Equation \(\ref{10.7.9}\), \(v_{\rm rms}\) has units of meters per second; consequently, the units of molar mass \(M\) are kilograms per mole, temperature \(T\) is expressed in kelvins, and the ideal gas constant \(R\) has the value 8.3145 J/(K•mol). Equation \(\ref{10.7.9}\) shows that \(v_{\rm rms}\) of a gas is proportional to the square root of its Kelvin temperature and inversely proportional to the square root of its molar mass. The root mean-square speed of a gas increase with increasing temperature. At a given temperature, heavier gas molecules have slower speeds than do lighter ones.
The rms speed and the average speed do not differ greatly (typically by less than 10%). The distinction is important, however, because the rms speed is the speed of a gas particle that has average kinetic energy. Particles of different gases at the same temperature have the same average kinetic energy, not the same average speed. In contrast, the most probable speed (vp) is the speed at which the greatest number of particles is moving. If the average kinetic energy of the particles of a gas increases linearly with increasing temperature, then Equation \(\ref{10.7.8}\) tells us that the rms speed must also increase with temperature because the mass of the particles is constant. At higher temperatures, therefore, the molecules of a gas move more rapidly than at lower temperatures, and vp increases.
At a given temperature, all gaseous particles have the same average kinetic energy but not the same average speed.
Example \(\PageIndex{1}\)
The speeds of eight particles were found to be 1.0, 4.0, 4.0, 6.0, 6.0, 6.0, 8.0, and 10.0 m/s. Calculate their average speed (\(v_{\rm av}\)) root mean square speed (\(v_{\rm rms}\)), and most probable speed (\(v_{\rm m}\)).
Given: particle speeds
Asked for: average speed (\(v_{\rm av}\)), root mean square speed (\(v_{\rm rms}\)), and most probable speed (\(v_{\rm m}\))
Strategy:
Use Equation \(\ref{10.7.6}\) to calculate the average speed and Equation \(\ref{10.7.8}\) to calculate the rms speed. Find the most probable speed by determining the speed at which the greatest number of particles is moving.
Solution:
The average speed is the sum of the speeds divided by the number of particles:
\[v_{\rm av}=\rm\dfrac{(1.0+4.0+4.0+6.0+6.0+6.0+8.0+10.0)\;m/s}{8}=5.6\;m/s \nonumber\]
The rms speed is the square root of the sum of the squared speeds divided by the number of particles:
\[v_{\rm rms}=\rm\sqrt{\dfrac{(1.0^2+4.0^2+4.0^2+6.0^2+6.0^2+6.0^2+8.0^2+10.0^2)\;m^2/s^2}{8}}=6.2\;m/s oumber\]
The most probable speed is the speed at which the greatest number of particles is moving. Of the eight particles, three have speeds of 6.0 m/s, two have speeds of 4.0 m/s, and the other three particles have different speeds. Hence \(v_{\rm m}=6.0\) m/s. The \(v_{\rm rms}\) of the particles, which is related to the average kinetic energy, is greater than their average speed.
Distributions of Molecular Speeds
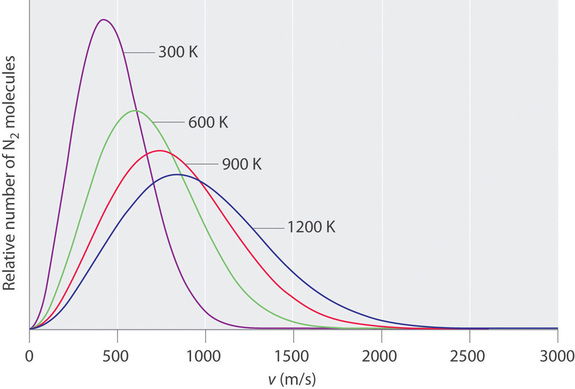
At any given time, what fraction of the molecules in a particular sample has a given speed? Some of the molecules will be moving more slowly than average, and some will be moving faster than average, but how many in each situation? Answers to questions such as these can have a substantial effect on the amount of product formed during a chemical reaction. This problem was solved mathematically by Maxwell in 1866; he used statistical analysis to obtain an equation that describes the distribution of molecular speeds at a given temperature. Typical curves showing the distributions of speeds of molecules at several temperatures are displayed in Figure \(\PageIndex{3}\). Increasing the temperature has two effects. First, the peak of the curve moves to the right because the most probable speed increases. Second, the curve becomes broader because of the increased spread of the speeds. Thus increased temperature increases the value of the most probable speed but decreases the relative number of molecules that have that speed. Although the mathematics behind curves such as those in Figure \(\PageIndex{3}\) were first worked out by Maxwell, the curves are almost universally referred to as Boltzmann distributions, after one of the other major figures responsible for the kinetic molecular theory of gases.
The Relationships among Pressure, Volume, and Temperature
We now describe how the kinetic molecular theory of gases explains some of the important relationships we have discussed previously.
- Pressure versus Volume: At constant temperature, the kinetic energy of the molecules of a gas and hence the rms speed remain unchanged. If a given gas sample is allowed to occupy a larger volume, then the speed of the molecules does not change, but the density of the gas (number of particles per unit volume) decreases, and the average distance between the molecules increases. Hence the molecules must, on average, travel farther between collisions. They therefore collide with one another and with the walls of their containers less often, leading to a decrease in pressure. Conversely, increasing the pressure forces the molecules closer together and increases the density, until the collective impact of the collisions of the molecules with the container walls just balances the applied pressure.
- Volume versus Temperature: Raising the temperature of a gas increases the average kinetic energy and therefore the rms speed (and the average speed) of the gas molecules. Hence as the temperature increases, the molecules collide with the walls of their containers more frequently and with greater force. This increases the pressure, unless the volume increases to reduce the pressure, as we have just seen. Thus an increase in temperature must be offset by an increase in volume for the net impact (pressure) of the gas molecules on the container walls to remain unchanged.
- Pressure of Gas Mixtures: Postulate 4 of the kinetic molecular theory of gases states that gas molecules exert no attractive or repulsive forces on one another. If the gaseous molecules do not interact, then the presence of one gas in a gas mixture will have no effect on the pressure exerted by another, and Dalton’s law of partial pressures holds.
Example \(\PageIndex{2}\)
The temperature of a 4.75 L container of N2 gas is increased from 0°C to 117°C. What is the qualitative effect of this change on the
- average kinetic energy of the N2 molecules?
- rms speed of the N2 molecules?
- average speed of the N2 molecules?
- impact of each N2 molecule on the wall of the container during a collision with the wall?
- total number of collisions per second of N2 molecules with the walls of the entire container?
- number of collisions per second of N2 molecules with each square centimeter of the container wall?
- pressure of the N2 gas?
Given: temperatures and volume
Asked for: effect of increase in temperature
Strategy:
Use the relationships among pressure, volume, and temperature to predict the qualitative effect of an increase in the temperature of the gas.
Solution:
- Increasing the temperature increases the average kinetic energy of the N2 molecules.
- An increase in average kinetic energy can be due only to an increase in the rms speed of the gas particles.
- If the rms speed of the N2 molecules increases, the average speed also increases.
- If, on average, the particles are moving faster, then they strike the container walls with more energy.
- Because the particles are moving faster, they collide with the walls of the container more often per unit time.
- The number of collisions per second of N2 molecules with each square centimeter of container wall increases because the total number of collisions has increased, but the volume occupied by the gas and hence the total area of the walls are unchanged.
- The pressure exerted by the N2 gas increases when the temperature is increased at constant volume, as predicted by the ideal gas law.
Exercise \(\PageIndex{2}\)
A sample of helium gas is confined in a cylinder with a gas-tight sliding piston. The initial volume is 1.34 L, and the temperature is 22°C. The piston is moved to allow the gas to expand to 2.12 L at constant temperature. What is the qualitative effect of this change on the
- average kinetic energy of the He atoms?
- rms speed of the He atoms?
- average speed of the He atoms?
- impact of each He atom on the wall of the container during a collision with the wall?
- total number of collisions per second of He atoms with the walls of the entire container?
- number of collisions per second of He atoms with each square centimeter of the container wall?
- pressure of the He gas?
- Answer a
-
no change
- Answer b
-
no change
- Answer c
-
no change
- Answer d
-
no change
- Answer e
-
decreases
- Answer f
-
decreases
- Answer g
-
decreases
Summary
- The kinetic molecular theory of gases provides a molecular explanation for the observations that led to the development of the ideal gas law.
- Average kinetic energy:\[ \left\langle {E_k}\right\rangle =\dfrac{1}{2}m{v_{\rm rms}}^2=\dfrac{3}{2}\dfrac{R}{N_A}T n\nonumber\]
- Root mean square speed: \[v_{\rm rms}=\sqrt{\dfrac{v_1^2+v_2^2+\cdots v_N^2}{N}} \nonumber\]
- Kinetic molecular theory of gases: \[v_{\rm rms}=\sqrt{\dfrac{3RT}{M}} \nonumber\]
The behavior of ideal gases is explained by the kinetic molecular theory of gases. Molecular motion, which leads to collisions between molecules and the container walls, explains pressure, and the large intermolecular distances in gases explain their high compressibility. Although all gases have the same average kinetic energy at a given temperature, they do not all possess the same root mean square (rms) speed (vrms). The actual values of speed and kinetic energy are not the same for all particles of a gas but are given by a Boltzmann distribution, in which some molecules have higher or lower speeds (and kinetic energies) than average.

